第三章图形的平移与旋转复习课件 -（北师大）

这是一份第三章图形的平移与旋转复习课件 -（北师大），共14页。

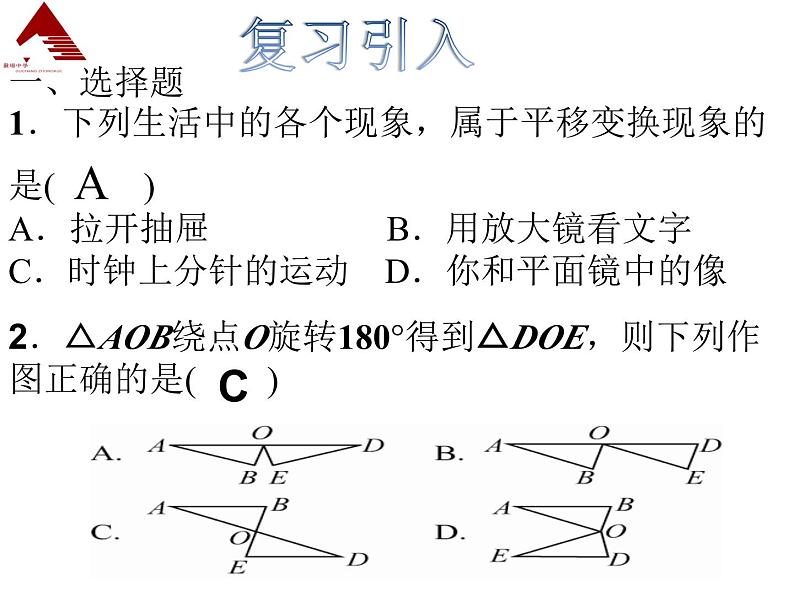
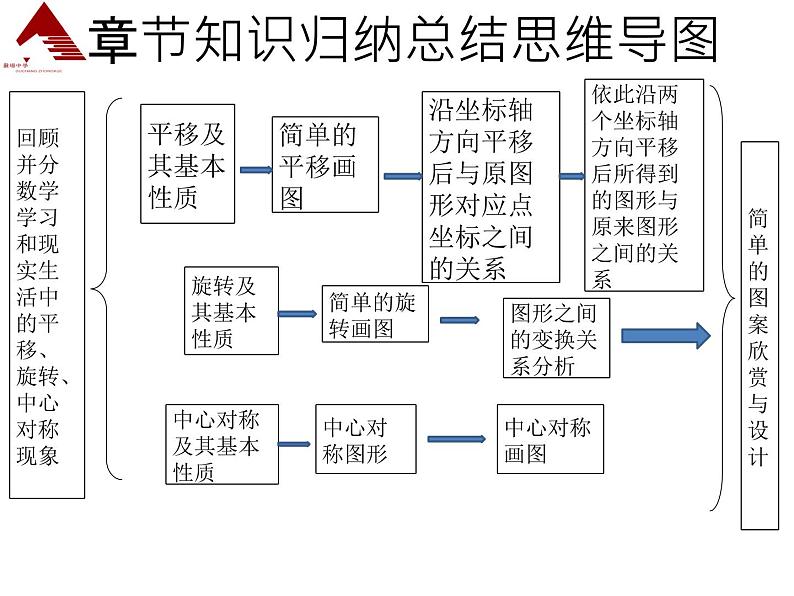
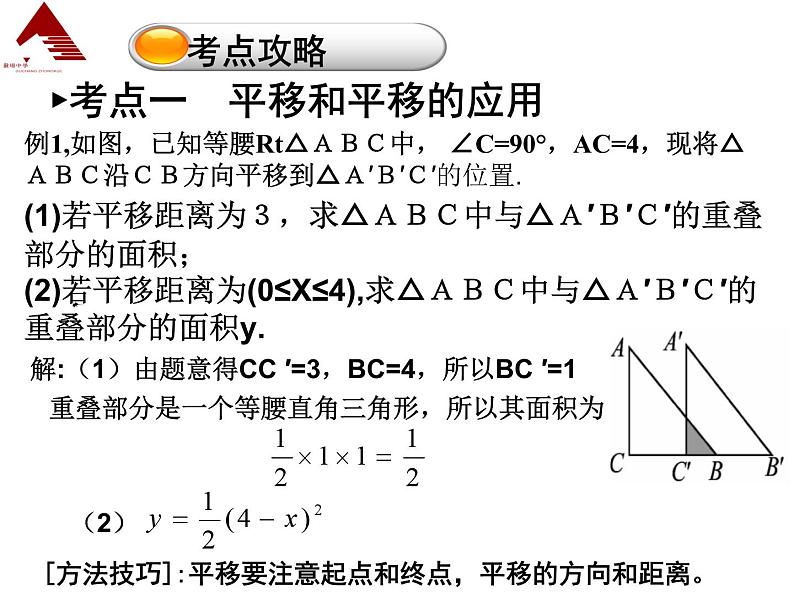
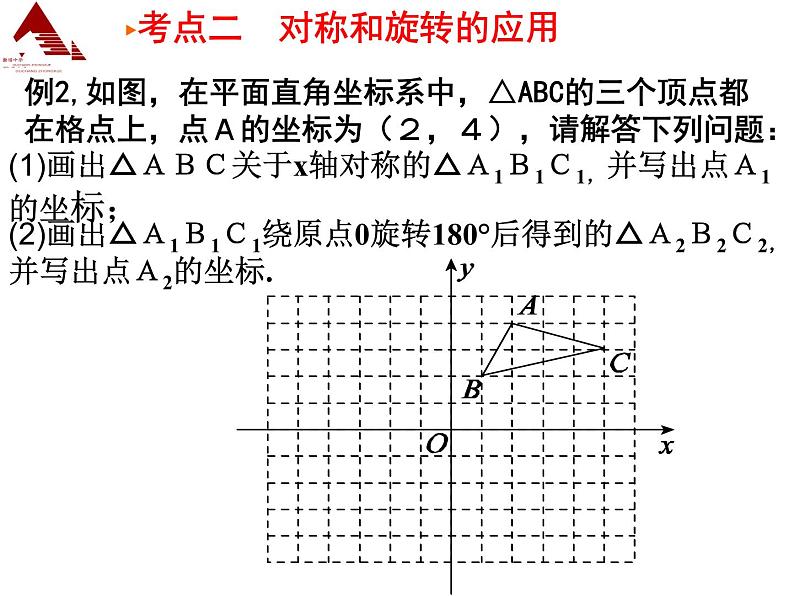
八年级下第三章复习课学习目标1、知识与技能：理解平移，旋转、中心对称的概念和性质，掌握坐标变化的特征。2、会运用平移、旋转、中心对称的相关知识解决问题。2．△AOB绕点O旋转180°得到△DOE，则下列作图正确的是(　　)一、选择题1．下列生活中的各个现象，属于平移变换现象的是(　　)A．拉开抽屉 B．用放大镜看文字 C．时钟上分针的运动 D．你和平面镜中的像复习引入AC3．下列说法中错误的是(　　)A．成中心对称的两个图形全等B．成中心对称的两个图形中，对应点的连线被对称中心平分C．中心对称图形的对称中心在对称轴上D．中心对称图形绕对称中心旋转180°后，都能与自身重合4．已知点A(a，1)与点B(－4，b)关于原点对称，则a＋b的值为(　　) A．5　 B．－5 　 C．3　 　 D．－3CC章节知识归纳总结思维导图 ►考点一　平移和平移的应用例1,如图，已知等腰Rt△ＡＢＣ中， ∠C=90°，AC=4，现将△ＡＢＣ沿ＣＢ方向平移到△Ａ′Ｂ′Ｃ′的位置.(1)若平移距离为３，求△ＡＢＣ中与△Ａ′Ｂ′Ｃ′的重叠部分的面积；(2)若平移距离为(0≤X≤4),求△ＡＢＣ中与△Ａ′Ｂ′Ｃ′的重叠部分的面积y.解:（1）由题意得CC ′=3，BC=4，所以BC ′=1重叠部分是一个等腰直角三角形，所以其面积为 [方法技巧]:平移要注意起点和终点，平移的方向和距离。►考点二　对称和旋转的应用例2,如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点Ａ的坐标为（２，４），请解答下列问题：(1)画出△ＡＢＣ关于x轴对称的△Ａ1Ｂ1Ｃ1，并写出点Ａ1的坐标；(2)画出△Ａ1Ｂ1Ｃ1绕原点0旋转180°后得到的△Ａ2Ｂ2Ｃ2，并写出点Ａ2的坐标.解:(1)△Ａ1Ｂ1Ｃ1如图所示， 点Ａ1的坐标为（2， － 4）.(2)△Ａ2Ｂ2Ｃ2 如图所示，点Ａ2的坐标为（ － 2,4）.例3.如图，已知△ABC与△CDA关于点O成中心对称，过点O任作直线EF分别交AD，BC于点E，F，下面的结论：①点E和点F，点B和点D分别关于点O中心对称；②直线BD必经过点O；③四边形ABCD是中心对称图形；④四边形DEOC与四边形BFOA的面积必相等；⑤△AOE与△COF成中心对称．其中正确的个数为(　　) A．2 B．3 C．4 D．5D►考点三 中心对称应用　（1）四边形A′B′C′D′与四边形ABCD对应点的横坐标有什么关系？纵坐标呢？分别写出点A′B′C′D′的坐标.（2）如果将四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的，请指出这一平移的平移方向和平移距离.小组合作探究——平移运用问题1：如图所示四边形ABCD各顶点的坐标为A（﹣3，5）、B（﹣4，3）、C（﹣1，1）、D（﹣1，4），将四边形ABCD先向上平移3个单位长度，再向右平移4个单位长度，得到四边形A′B′C′D′.解：（1）四边形A′B′C′D′与四边形ABCD相比，对应点的横坐标分别增加了4，纵坐标分别增加了3, A′（1,8）、B′（0,6）、C′（3,4）、D′（3,7）。（2）连接AA′，由图可知，AA′= 5，四边形A′B′C′D′可认为是由四边形ABCD沿着由A到A′的方向，平移5个单位长度得到的.解：(1)旋转中心是A，旋转角∠ＣＡＢ＝ ∠ ＤＡＤ′=90°(2)AD与AＤ′、AB与AC、DB与Ｄ′C是对应线段(3)△ADＤ′是等腰直角三角形问题2、如图，D是等腰Rt △ABc内一点，Bc是斜边，如果△ ABD绕点Ａ按逆时针方向旋转到△ AcＤ′的位置，则：(1) 旋转中心是什么？指出旋转角及其度数 (2) 指出旋转图行中的对应线段(3) 判断△ADＤ′的形状旋转针对训练小组合作探究中心对称运用问题3.如图，△ABO与△ CDO关于O点中心对称，点Ｅ，F在线段AC上，且AF＝CE.求证：FD=BE.证明：△ABO与△ CDO关于O点中心对称，∴OB＝OD，OA=OC.∵AF=CE,∴OF=OE.在△DOF和△BOE中，OD=OB∠DOF= ∠BOEOF=OE.∴ △DOF ≌ △BOE∴FD=BE1.从教材习题中选取2.完成练习册本课时的习题布置作业