



还剩15页未读,
继续阅读
所属成套资源:第五章分式与分式方程 小结与复习 -(北师大)
成套系列资料,整套一键下载
第五章分式复习课件 -(北师大)
展开
这是一份第五章分式复习课件 -(北师大),共23页。
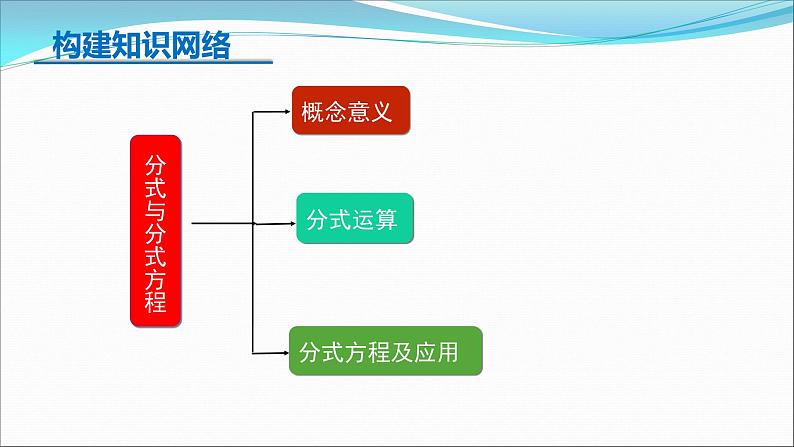
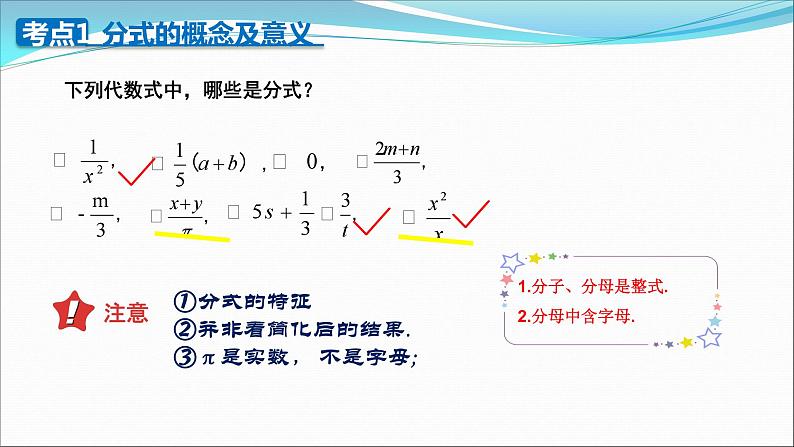
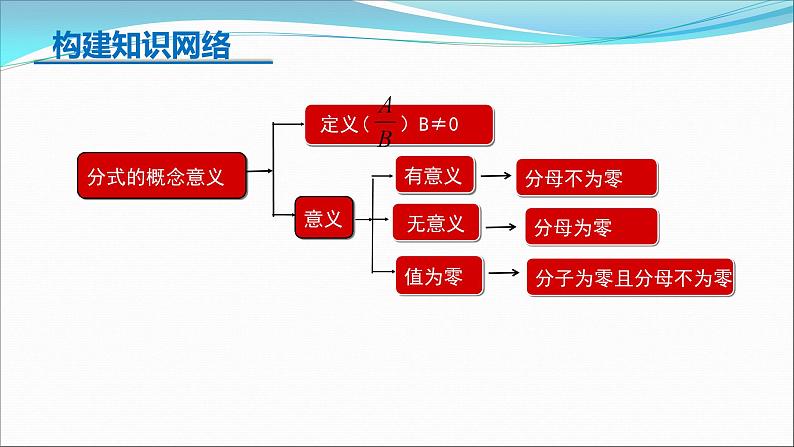
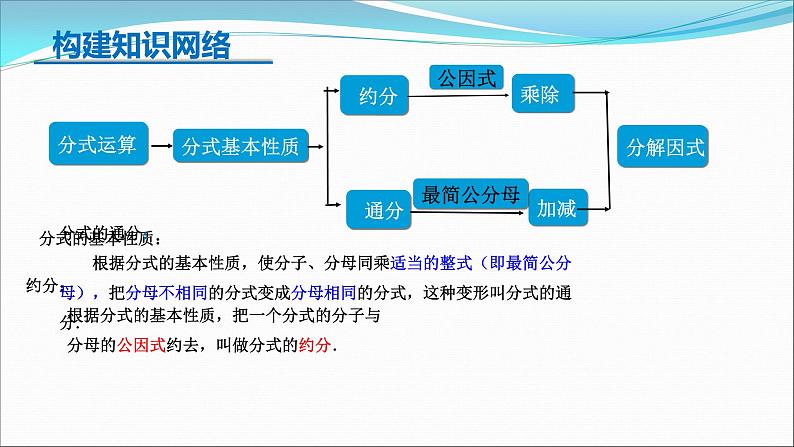
八年级下册 第五章 分式复习分式与分式方程概念意义 构建知识网络 下列代数式中,哪些是分式?分式的特征并非看简化后的结果.π是实数, 不是字母;分母不为零分母为零分子为零且分母不为零 构建知识网络分式的概念及意义x≠-3 x>3【思路点拨】分式的值为0必须同时满足两个条件:分子为0,分母不为0.【自主解答】选D.由题意,得x2-9=0,解得x=±3,又3x+9≠0,所以x≠-3,所以x=3.【解析】由题意,得分母x-2≠0,解得x≠2.跟踪练习约分: 根据分式的基本性质,把一个分式的分子与 分母的公因式约去,叫做分式的约分.分式的通分: 根据分式的基本性质,使分子、分母同乘适当的整式(即最简公分母),把分母不相同的分式变成分母相同的分式,这种变形叫分式的通分. 构建知识网络分式的性质及有关计算BC跟踪练习分式的性质及有关计算 【解析】原式分式的乘除法则:除变乘分解因式约分最简分式分式的性质及有关计算【例5】.计算: = .【解析】原式=分式的加减法则:(1)同分母分式的加减法则:(2)异分母分式的加减法则: 有一道题:“先化简,再求值: ,其中 ”.小玲做题时把 错抄成 ,但她的计算结果也是正确的,请你解释这是怎么回事?解:∴结果与x的符号无关跟踪练习练习4:先算乘方,再算乘除,最后算加减,有括号的先算括号里面的. 构建知识网络 【例7】 解分式方程的一般步骤 (1)去分母,化成整式方程. (2)解这个整式方程. (3)验根 (4)写出原方程的根.解:最简公分母为(x+2)(x-2),去分母得(x-2)2-(x+2)(x-2)=16,整理得-4x+8=16,解得x=-2,经检验x=-2是增根,故原分式方程无解.练习5: 解分式方程跟踪练习解:去分母,两边都乘以(x+2)(x-2),得3(x-2)+2=x+2,解得x=3.经检验x=3是原方程的根.解:去分母,两边同乘以(x+1)(x-1),得3(x-1)=x(x+1)-(x+1)(x-1).解得x=2.检验:当x=2时,(x+1)(x-1)≠0,∴原方程的解是x=2.【例8】. .某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3 600米道 路的任务,按原计划完成总任务的三分之一后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务,原计划每小时抢修道路多少米?【思路点拨】设未知数→列方程→去分母→解整式方程→验根并作答.练习6:某班在“世界读书日”开展了图书交换活动,第一组同学共带图书24本,第二组同学共带图书27本,已知第一组同学比第二组同学平均每人多带1本书,第二组人数是第一组人数的1.5倍,求第一组的人数.分式与分式方程概念意义 构建知识网络ACC5.先化简: 然后解答下列问题:(1)当x=3时,求代数式的值;(2)原代数式的值能等于-1吗?为什么?
八年级下册 第五章 分式复习分式与分式方程概念意义 构建知识网络 下列代数式中,哪些是分式?分式的特征并非看简化后的结果.π是实数, 不是字母;分母不为零分母为零分子为零且分母不为零 构建知识网络分式的概念及意义x≠-3 x>3【思路点拨】分式的值为0必须同时满足两个条件:分子为0,分母不为0.【自主解答】选D.由题意,得x2-9=0,解得x=±3,又3x+9≠0,所以x≠-3,所以x=3.【解析】由题意,得分母x-2≠0,解得x≠2.跟踪练习约分: 根据分式的基本性质,把一个分式的分子与 分母的公因式约去,叫做分式的约分.分式的通分: 根据分式的基本性质,使分子、分母同乘适当的整式(即最简公分母),把分母不相同的分式变成分母相同的分式,这种变形叫分式的通分. 构建知识网络分式的性质及有关计算BC跟踪练习分式的性质及有关计算 【解析】原式分式的乘除法则:除变乘分解因式约分最简分式分式的性质及有关计算【例5】.计算: = .【解析】原式=分式的加减法则:(1)同分母分式的加减法则:(2)异分母分式的加减法则: 有一道题:“先化简,再求值: ,其中 ”.小玲做题时把 错抄成 ,但她的计算结果也是正确的,请你解释这是怎么回事?解:∴结果与x的符号无关跟踪练习练习4:先算乘方,再算乘除,最后算加减,有括号的先算括号里面的. 构建知识网络 【例7】 解分式方程的一般步骤 (1)去分母,化成整式方程. (2)解这个整式方程. (3)验根 (4)写出原方程的根.解:最简公分母为(x+2)(x-2),去分母得(x-2)2-(x+2)(x-2)=16,整理得-4x+8=16,解得x=-2,经检验x=-2是增根,故原分式方程无解.练习5: 解分式方程跟踪练习解:去分母,两边都乘以(x+2)(x-2),得3(x-2)+2=x+2,解得x=3.经检验x=3是原方程的根.解:去分母,两边同乘以(x+1)(x-1),得3(x-1)=x(x+1)-(x+1)(x-1).解得x=2.检验:当x=2时,(x+1)(x-1)≠0,∴原方程的解是x=2.【例8】. .某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3 600米道 路的任务,按原计划完成总任务的三分之一后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务,原计划每小时抢修道路多少米?【思路点拨】设未知数→列方程→去分母→解整式方程→验根并作答.练习6:某班在“世界读书日”开展了图书交换活动,第一组同学共带图书24本,第二组同学共带图书27本,已知第一组同学比第二组同学平均每人多带1本书,第二组人数是第一组人数的1.5倍,求第一组的人数.分式与分式方程概念意义 构建知识网络ACC5.先化简: 然后解答下列问题:(1)当x=3时,求代数式的值;(2)原代数式的值能等于-1吗?为什么?
相关资料
更多









