2022-2023学年江苏省扬州市高邮市五校八年级（下）期中数学试卷（含解析）

这是一份2022-2023学年江苏省扬州市高邮市五校八年级（下）期中数学试卷（含解析），共27页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年江苏省扬州市高邮市五校八年级（下）期中数学试卷
一、选择题（本大题共8小题，共24.0分。在每小题列出的选项中，选出符合题目的一项）
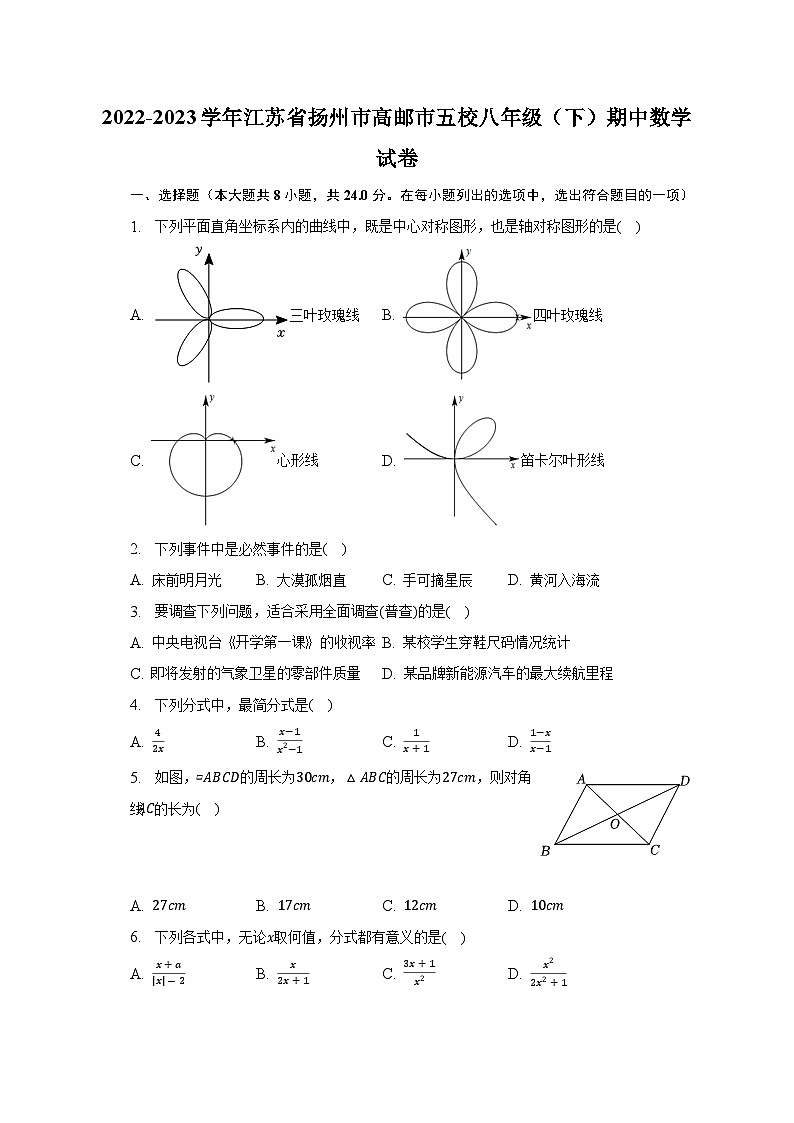
1. 下列平面直角坐标系内的曲线中，既是中心对称图形，也是轴对称图形的是(    )
A. 三叶玫瑰线 B. 四叶玫瑰线
C. 心形线 D. 笛卡尔叶形线
2. 下列事件中是必然事件的是(    )
A. 床前明月光 B. 大漠孤烟直 C. 手可摘星辰 D. 黄河入海流
3. 要调查下列问题，适合采用全面调查(普查)的是(    )
A. 中央电视台《开学第一课》的收视率 B. 某校学生穿鞋尺码情况统计
C. 即将发射的气象卫星的零部件质量 D. 某品牌新能源汽车的最大续航里程
4. 下列分式中，最简分式是(    )
A. 42x B. x−1x2−1 C. 1x+1 D. 1−xx−1
5. 如图，▱ABCD的周长为30cm，△ABC的周长为27cm，则对角线AC的长为(    )


A. 27cm B. 17cm C. 12cm D. 10cm
6. 下列各式中，无论x取何值，分式都有意义的是(    )
A. x+a|x|-2 B. x2x+1 C. 3x+1x2 D. x22x2+1
7. 如图，矩形ABCD中，边AB=4，BC=8，P、Q分别是边BC、AD上的点，且四边形APCQ是菱形，则菱形的面积为(    )


A. 10 B. 12 C. 16 D. 20
8. 如图，在四边形ABCD中，∠A=∠B=90°，AB=BC=4，AD=3，E是边AB上一点，且∠DCE=45°，则DE的长度是(    )
A. 3.2
B. 3.4
C. 3.6
D. 4
二、填空题（本大题共10小题，共30.0分）
9. 分式12x2y,16xy3的最简公分母是______．
10. 某次列车平均提速vkm/h，用相同的时间，列车提速前行驶skm，提速后比提速前多行驶50km，可求得提速前列车的平均速度为______km/h．
11. 若分式x−1x−5的值为0，则x的值为______ ．
12. 木箱里装有仅颜色不同的8张红色和若干张蓝色卡片，随机从木箱里摸出1张卡片记下颜色后再放回，经过多次的重复试验，发现摸到蓝色卡片的频率稳定在0.6附近，则估计木箱中蓝色卡片有______张．
13. 如图，平行四边形ABCD的周长为36，对角线AC、BD相交于点O，点E是CD的中点，BD=14，则△DOE的周长为______．


14. 如图，将△ABC绕点A顺时针旋转60°得到△AED.若线段AB=3，则△ABE的周长等于______．


15. 如图，已知坐标原点O为平行四边形ABCD的对角线AC的中点，顶点A的横坐标为4，AD平行x轴，且AD长为5.若平行四边形面积为10，则顶点B的坐标为______．


16. 已知关于x的分式方程a+2x+1=1的解是非正数，则a的取值范围是______ ．
17. 如图，在平行四边形ABCD中，点E，F分别是AD，BC边的中点，延长CD至点G，使DG=CD，以DG，DE为边向平行四边形ABCD外构造平行四边形DGME，连接BM交AD于点N，连接FN.若DG=DE=2，∠ADC=60°，则FN的长为______ ．

18. 如图，在等边三角形ABC中，AB=4，P为AC上一点(与点A、C不重合)，连接BP，以PA、PB为邻边作平行四边形PADB，则PD的取值范围是______．


三、解答题（本大题共10小题，共80.0分。解答应写出文字说明，证明过程或演算步骤）
19. (本小题8.0分)
计算：
(1)aa−b−bb−a；
(2)x−4x+3÷(x−3−7x+3)．
20. (本小题8.0分)
已知a2+2a−1=0，求代数式(a2−1a2−2a+1−11−a)÷1a2−a的值．
21. (本小题8.0分)
在一个不透明的口袋里装有n个相同的红球，为了估计袋中红球的数量，八(1)学生利用数学实验分组做摸球试验：现将10个与红球大小形状完全相同的白球装入袋中，搅匀后从中随机摸出一个并记下颜色，再把它放回袋中，不断重复，表是统计汇总各小组数据后获得的全班数据统计表：
摸球的次数
150
300
600
900
1260
1500
摸到白球的频数
60
a
247
365
484
609
摸到白球的频率
0.400
0.42
0.412
0.406
0.403
b
(1)按表格数据格式，表中的a= ______ ，b= ______ ；
(2)请推算：摸到红球的概率是______ (精确到0.1)；
(3)试估算：这个不透明的口袋中红球的数量n的值．
22. (本小题8.0分)
在“世界读书日”前夕，某校开展了“共享阅读，向上人生”的读书活动.活动中，为了解学生对书籍种类(A：艺术类，B：科技类，C：文学类，D：体育类)的喜欢情况，学生会在全校范围内随机抽取若干名学生，进行问卷调查(每个被调查的学生必须选择并且只能在这四种类型中选择一项)将数据进行整理并绘制成下面两幅不完整的统计图．

(1)这次调查中，一共调查了______ 名学生．
(2)求扇形统计图中“D”所在扇形圆心角的度数，并补全条形统计图；
(3)若全校有2600名学生，请估计喜欢B类书籍的学生约有多少名？
23. (本小题8.0分)
如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的顶点均在格点上．
(1)画出将△ABC关于原点O的中心对称图形△A1B1C1．
(2)将△DEF绕点E顺时针旋转90°得到△D1EF1，画出△D1EF1．
(3)若△DEF由△ABC绕着某点旋转得到的，则这点的坐标为______ ．

24. (本小题8.0分)
列方程解决问题：
某校利用暑假进行田径场的改造维修，项目承包单位派遣一号施工队进场施工，计划用30天时间完成整个工程.当一号施工队工作10天后，承包单位接到通知，有一大型活动要在该田径场举行，要求比原计划提前8天完成整个工程，于是承包单位派遣二号与一号施工队共同完成剩余工程，结果按通知要求如期完成整个工程.若二号施工队单独施工，完成整个工程需要多少天？
25. (本小题8.0分)
如图，已知平行四边形ABCD中，BD是它的一条对角线，过A、C两点作AE⊥BD，CF⊥BD，垂足分别为E、F，延长AE、CF分别交CD、AB于点M、N．
(1)求证：四边形CMAN是平行四边形
(2)已知DE=8，FN=6，求BN的长．

26. (本小题8.0分)
已知线段AB，BC，∠ABC=90°.求作：矩形ABCD.(要求：用直尺和圆规作图，不写作法，保留作图痕迹)
(1)请用一种方法，在图1上作出矩形ABCD；
(2)请用另一种方法，在图2上作出矩形ABCD；
(3)根据你所作的图形，选择其中一个，证明四边形ABCD是矩形．

27. (本小题8.0分)
阅读：
对于两个不等的非零实数a、b，若分式(x−a)(x−b)x的值为零，则x=a或x=b.又因为(x−a)(x−b)x=x2−(a+b)x+abx=x+abx−(a+b)，所以关于x的方程x+abx=a+b有两个解，分别为x1=a，x2=b．
应用上面的结论解答下列问题：
(1)方程x+px=q的两个解分别为x1=−2、x2=3，则p=______，q=______；
(2)方程x+7x=8的两个解中较大的一个为______；
(3)关于x的方程2x+n2−n2x−1=2n的两个解分别为x1，x2(x1