
2023年贵州省遵义市仁怀市中考数学第一次适应性试卷(含解析)
展开1. 3的相反数是( )
A. −3B. −13C. 3D. 13
2. 如图所示图形既是中心对称图形也是轴对称图形的是( )
A. B.
C. D.
3. 由如图所示三视图得到的立体图形是( )
A. 长1cm宽1cm高3cm的长方体B. 长1cm宽3cm高1cm的长方体
C. 长3cm宽1cm高3cm的长方体D. 长3cm宽1cm高1cm的长方体
4. 下列计算正确的是( )
A. a3⋅a5=a15B. (a2b3)2=a4b6
C. b6÷b2=b3D. a6b2÷a2b=a3b2
5. 一组数据:4,5,6,6,6,7,8,下列描述错误的是( )
A. 中位数是6B. 众数是6C. 平均数是6D. 方差是1.4
6. 在数轴上表示不等式3(x+1)2≥3的解集,正确的是( )
A. B.
C. D.
7. 如图,一副三角板的两条直角边互相重合,则∠1=( )
A. 60°
B. 75°
C. 90°
D. 105°
8. 下列计算正确的是( )
A. 2+ 5= 7B. 3× 6= 18
C. 2 3×3 3=18D. 1÷ 3=1 3
9. 下列是在同一直角坐标系中函数y1=k1x+b和y2=k2x的图象如图,其中k1,k2,b的描述正确的是( )
A. k1>0,k2>0,b>0
B. k1>0,k2<0,b>0
C. k1>0,k2>0,b<0
D. k1>0,k2<0,b<0
10. 如图,点A、B、C三点在⊙O上,点D为弦AB的中点,AB=8cm,CD=6cm,则OD=( )
A. 43cm
B. 53cm
C. 83cm
D. 103cm
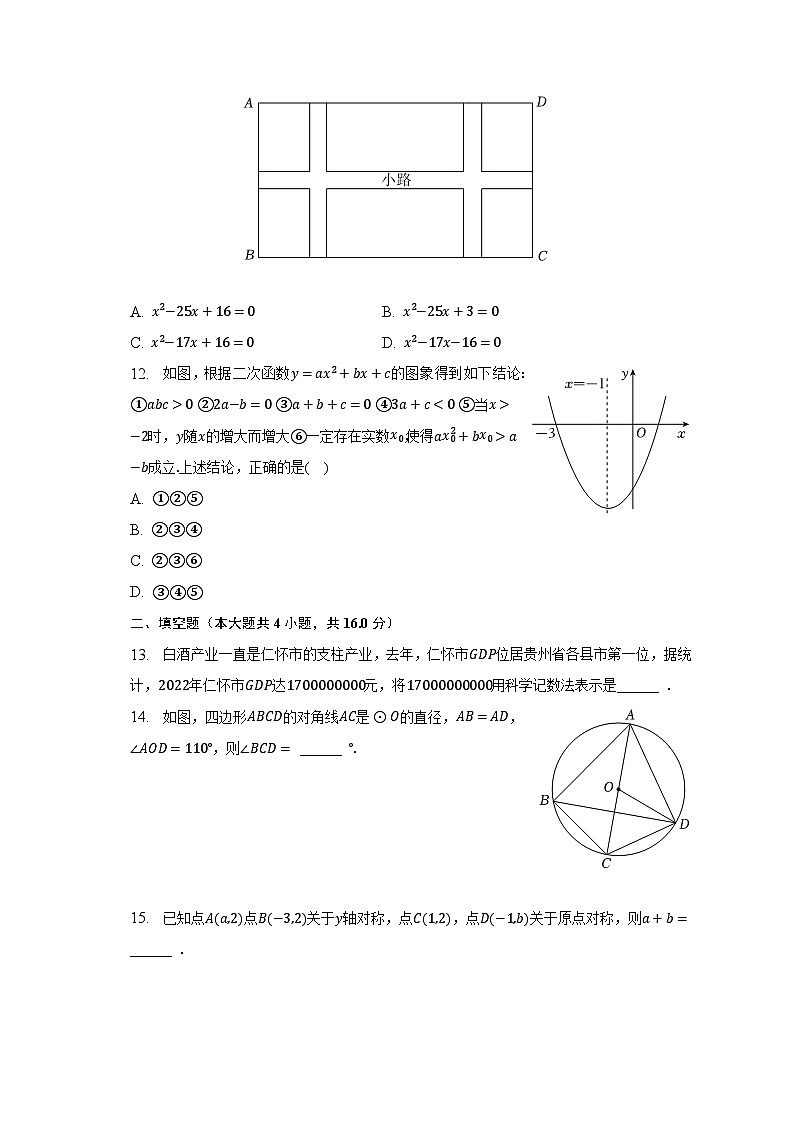
11. 如图,某小区计划在一个长16m,宽9m的长方形场地上修建同样宽的小路,使其中两条与AB平行,另一条与BC平行,其余部分种草.如果使草坪部分的总面积为112m2,设小路的宽为x m,那么x满足的方程是( )
A. x2−25x+16=0B. x2−25x+3=0
C. x2−17x+16=0D. x2−17x−16=0
12. 如图,根据二次函数y=ax2+bx+c的图象得到如下结论:①abc>0 ②2a−b=0 ③a+b+c=0 ④3a+c<0 ⑤当x>−2时,y随x的增大而增大⑥一定存在实数x0,使得ax02+bx0>a−b成立.上述结论,正确的是( )
A. ①②⑤
B. ②③④
C. ②③⑥
D. ③④⑤
二、填空题(本大题共4小题,共16.0分)
13. 白酒产业一直是仁怀市的支柱产业,去年,仁怀市GDP位居贵州省各县市第一位,据统计,2022年仁怀市GDP达1700000000元,将17000000000用科学记数法表示是______ .
14. 如图,四边形ABCD的对角线AC是⊙O的直径,AB=AD,∠AOD=110°,则∠BCD= ______ °.
15. 已知点A(a,2)点B(−3,2)关于y轴对称,点C(1,2),点D(−1,b)关于原点对称,则a+b= ______ .
16. 如图,在边长为6的正方形ABCD中,点E,F分别是AB,BC边的中点,连接CE,DF,点C,H分别是CE,FD的中点,连接GH,则GH= ______ .
三、解答题(本大题共9小题,共98.0分。解答应写出文字说明,证明过程或演算步骤)
17. (本小题12.0分)
(1)计算:(π−3.14)0−|1− 2|−(12)−2+3−8;
(2)有三个不等式:2x+3<1;3(x−1)>6;−2x>6.请在其中任选两个不等式,组成一个不等式组,并求出它的解集.
18. (本小题8.0分)
以下是小明化简分式(xx2+x−1)÷x2−1x2+2x+1的过程.
解:原式=(xx2+x−x2+xx2+x)÷x2−1x2+2x+1…第一步
=(x−x2+xx2+x)×x2+2x+1x2−1…第二步
=−x(x−2)(x+1)2x(x+1)2(x−1)…第三步
=2−xx−1…第四步
(1)小明的解答过程在第______ 步开始出错;
(2)请写出正确的解答过程.
19. (本小题10.0分)
如图1,四边形ABCD是平行四边形,∠ABC的平分线交AD边于点E、交CD边的延长线于点G,过点E作EF//DG,过点C作FG//AD.
(1)求证:四边形DEFG是菱形;
(2)如图2,若∠ABC=120°,BC=6cm,点E是BG的中点,求菱形DEFG的面积.
20. (本小题12.0分)
全国中考改革,2023年开始,由原来的各地州统考改为全省统考.为此,某学校为了了解九年级学生的学习状态,随机抽取了部分学生对自己最喜欢的科目进行调查(每个学生必选一项且只能选一项),制定了如图不完整的统计图,请根据统计图回答问题:
(1)补全条形图,计算扇形统计图中,英语学科所占扇形的圆心角是______ 度.
(2)若该学校有1200名师生,请估计最喜欢物理学科的学生有多少?
(3)若从最喜欢体育学科的3名男生和1名女生中随机抽取两名同学测试其体能,请用树状图或列表法求刚好抽到1名男生和1名女生的概率.
21. (本小题8.0分)
某超市投入12800元的资金购进甲、乙两种饮料共500箱,饮料的成本和售价如表所示:
(1)该超市购进甲、乙两种饮料各多少箱?
(2)全部售完500箱饮料,该超市共获得利润多少元?
22. (本小题12.0分)
如图,已知△ABC和△CDE是等边三角形,点B,点C,点E在同一条直线上,连接BD,AE交于点F.
(1)求证:BD=AE;
(2)求∠AFB的度数;
(3)连接FC,求证:FC平分∠EFB.
23. (本小题10.0分)
近年来,仁怀市坛厂镇的八卦园旅游项目深受游客喜欢,每年3月份,“坐彩虹滑道,闻满园油菜花香”是一件令游客追捧的项目.彩虹滑道是一个修建在水平地面上的游玩设备,由助跑段、缓冲段、着陆段、终点共四部分组成.如图2是某个数学爱好者根据彩虹滑道图1抽象出来的示意图.已知:助跑段AF=40米,缓冲段的跨度FG=20米,顶端E到BD的距离为20米,HG//BC,∠AFH=45°,∠EFG=25°,∠ECB=30°.求此彩虹滑道最高点A距地面BD的距离是多少米(结果保留整数).
(参考数据:sin25°≈0.42,cs25°≈0.91,tan25°≈0.47, 2≈1.41, 3≈1.73)
24. (本小题12.0分)
如图,在正方形ABCD中,以CD边为直径作⊙O,在⊙O的左半圆上取点E,使得BA=BE,延长BE交AD边于点F.
(1)将图形补充完整(不写作法,保留作图痕迹);
(2)证明:BE是⊙O的切线;
(3)若⊙O半径为2,求CE的长.
25. (本小题14.0分)
如图1,在平面直角坐标系中,直线y=−x+4交两坐标轴于B、C两点,二次函数y=ax2+bx+c图象经过A,B,C三点且A(−1,0).
(1)求二次函数的解析式.
(2)在抛物线的对称轴上是否存在点P?使得PA+PC的长度最短.若存在,求出点P的坐标;若不存在,请说明理由.
(3)在直线上方抛物线上是否存在点Q?使得△QBC的面积有最大值.若存在,求出点Q的坐标及此时△QBC的面积;若不存在,请说明理由.
答案和解析
1.【答案】A
【解析】解:根据概念,3的相反数在3的前面加“−“号,则3的相反数是−3.
故选:A.
本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“−”号:一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.
2.【答案】C
【解析】解:A.原图是轴对称图形,不是中心对称图形,故此选项不合题意;
B.原图是中心对称图形,不是轴对称图形,故此选项不合题意;
C.原图既是中心对称图形,也是轴对称图形,故此选项符合题意;
D.原图是轴对称图形,不是中心对称图形,故此选项不合题意;
故选:C.
根据中心对称图形与轴对称图形的概念进行判断即可.
本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与自身重合.
3.【答案】D
【解析】解:观察图形可知,由如图所示三视图得到的立体图形是长3cm宽1cm高1cm的长方体.
故选:D.
由三视图想象几何体的形状,首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.依此即可求解.
本题考查由三视图判断几何体,根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,以及几何体的长、宽、高.
4.【答案】B
【解析】解:A.a3⋅a5=a8,故此选项不合题意;
B.(a2b3)2=a4b6,故此选项符合题意;
C.b6÷b2=b4,故此选项不合题意;
D.a6b2÷a2b=a4b,故此选项不合题意.
故选:B.
直接利用同底数幂的乘法运算、单项式乘除单项式、积的乘方运算法则分别判断,进而得出答案.
此题主要考查了同底数幂的乘法运算、单项式乘除单项式、积的乘方运算,正确掌握相关运算法则是解题关键.
5.【答案】D
【解析】解:A、把这些数从小到大排列为:4,5,6,6,6,7,8,则中位数是6,故本选项不符合题意;
B、6出现了3次,出现的次数最多,所以众数是6,故本选项不符合题意;
C、平均数是(4+5+6+6+6+7+8)÷7=6,故本选项不符合题意;
D、方差为:17×[(4−6)2+(5−6)2+(6−6)2+(6−6)2+(6−6)2+(7−6)2+(8−6)2]=107,故本选项符合题意.
故选:D.
根据众数、平均数、中位数、方差的定义和公式分别进行计算即可.
本题考查了众数、平均数、中位数、方差.一组数据中出现次数最多的数据叫做众数.平均数是指在一组数据中所有数据之和再除以数据的个数.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.
6.【答案】C
【解析】解:3(x+1)2≥3,
3(x+1)≥6,
x+1≥2,
x≥1,
∴该不等式的解集在数轴上表示如图所示:
故选:C.
按照解一元一次不等式的步骤,进行计算即可解答.
本题考查了解一元一次不等式,在数轴上表示不等式的解集,熟练掌握解一元一次不等式的步骤是解题的关键.
7.【答案】B
【解析】解:如图:
在△ABC中,∠ACB=45°,∠ABC=60°,
∴∠CAB=180°−45°−60°=75°,
∴∠1=∠CAB=75°.
故选:B.
在△ABC中,∠ACB=45°,∠ABC=60°,利用三角形的内角和即可得出∠CAB的度数,即可求出∠1的度数.
本题主要考查了三角形的内角和,熟知三角形的内角和是解题的关键.
8.【答案】C
【解析】解:A、不是同类二次根式,不能合并,故A不符合题意;
B、原式=3 2,故B不符合题意;
C、原式=18,故C符合题意;
D、原式= 33,故D不符合题意.
故选:C.
根据二次根式的加法和乘除法法则,分母有理化计算即可求解.
本题考查了二次根式的混合运算,涉及二次根式的加法和乘除法,分母有理化等知识,正确的计算是解题的关键.
9.【答案】A
【解析】解:根据一次函数图象过一、二、三象限可知:k1>0,b>0,
根据反比例函数图象过一、三象限可知:k2>0,
∴k1>0,b>0,k2>0,
故选:A.
根据图象上一次函数和反比例函数的性质就可得出判断.
本题考查反比例函数、一次函数图象上点的坐标特征以及一次函数与反比例图象交点坐标,掌握一次函数和反比例函数的性质是解题关键.
10.【答案】B
【解析】解:连接OA,
设OA=r(cm),
则OC=OA=r(cm),
∵点D为弦AB的中点,O为圆心,
∴OD⊥AB,
∵AB=8(cm),
∴AD=BD=4(cm),
∵CD=6(cm),
∴OD=CD−OC=(6−r)(cm),
在Rt△AOD中,由勾股定理得OA2=OD2+AD2,
∴r2=(6−r)2+42,
解得r=133,
∴OD=53(cm),
故选:B.
连接OA,设OA=r(cm),根据CD的长计算出OD的长,根据点D为弦AB的中点,O为圆心得到OD⊥AB,从而求出AD的长,在Rt△AOD中利用勾股定理求出r的值,即可求出OD的长.
本题考查了垂径定理及推论,熟知:垂直于弦的直径平分这条弦,熟练掌握勾股定理的计算.
11.【答案】C
【解析】解:∵小路的宽为x m,
∴种草的部分可合成长为(16−2x)m,宽为(9−x)m的长方形.
根据题意得:(16−2x)(9−x)=112,
整理得:x2−17x+16=0.
故选:C.
由小路的宽为xm,可得出种草的部分可合成长为(16−2x)m,宽为(9−x)m的长方形,结合草坪部分的总面积为112m2,可得出关于x的一元二次方程,整理后即可得出结论.
本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
12.【答案】C
【解析】解:∵抛物线开口向上、顶点在y轴左侧、抛物线与y轴交于负半轴,
∴a>0,b>0,c<0,
∴abc<0,故①错误;
∵−b2a=−1,
∴b=2a,
∴2a−b=0,故②正确;
∵抛物线过点(−3,0),对称轴为直线x=−1,
∴抛物线过点(1,0),
∴a+b+c=0,故③正确;
∴b=2a,a+b+c=0,
∴3a+c=0,故④错误;
∵抛物线开口向上,对称轴是直线x=−1,
∴当x>−1时,y随x的增大而增大;故⑤错误;
∵函数最小值为a−b+c,
∴当x0≠−1时,则ax02+bx0+c>a−b+c,即ax02+bx0>a−b,
∴一定存在实数x0,使得ax02+bx0>a−b成立,故⑥正确;
故选:C.
由开口方向、对称轴及抛物线与y轴的交点位置可判断结论①;由对称轴为直线x=−1即可得到,2a−b=0,即可判断②;由抛物线的对称性即可判断③④;由抛物线的增减性可判断结论⑤;函数的最值即可判断结论⑥.
本题考查了二次函数图象与系数之间的关系,熟练掌握二次函数的开口方向,对称轴,图象与y轴交点,函数增减性并会综合运用是解决本题的关键.
13.【答案】1.7×1010
【解析】解:17000000000=1.7×1010.
故答案为:1.7×1010.
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
14.【答案】110
【解析】解:∵AB=AD,
∴AB=AD,
∴∠ACB=∠ACD,
∴∠BCD=2∠ACD,
∵∠AOD=2∠ACD,
∴∠BCD=∠AOD,
∵∠AOD=110°,
∴∠BCD=110°.
故答案为:110.
由AB=AD,得到AB=AD,因此∠ACB=∠ACD,故∠BCD=2∠ACD,由圆周角定理得到∠AOD=2∠ACD,因此∠BCD=∠AOD=110°.
本题考查圆周角定理,圆心角、弧、弦的关系,关键是由圆周角定理推出∠BCD=2∠ACD,∠AOD=2∠ACD,从而得到∠BCD=∠AOD.
15.【答案】1
【解析】解:∵点A(a,2)点B(−3,2)关于y轴对称,
∴a=3.
∵点C(1,2),点D(−1,b)关于原点对称,
∴b=−2,
∴a+b=3−2=1.
故答案为:1.
根据关于y轴对称的两点纵坐标不变,横坐标互为相反数;关于原点对称的两点横纵坐标与原来的互为相反数求出a、b,再代入计算即可.
本题考查了关于y轴对称的点的坐标以及关于原点对称的点的坐标特点,这一类题目是需要识记的基础题,解决的关键是对知识点的正确记忆.
16.【答案】 2
【解析】解:连接CH并延长交AD于P,连接PE,
∵四边形ABCD是正方形,
∴∠A=90°,AD//BC,AB=AD=BC=6,
∵E,F分别是边AB,BC的中点,
∴AE=CF=12×6=3,
∵AD//BC,
∴∠DPH=∠FCH,
在△PDH和△CFH中,
∠DPH=∠FCH∠DHP=∠FHCPH=FH,
∴△PDH≌△CFH(AAS),
∴PD=CF=3,
∴AP=AD−PD=3,
∴PE= AP2+AE2=3 2,
∵点G,H分别是EC,FD的中点,
∴GH=12EP=3 22.
故答案为:3 22.
连接CH并延长交AD于P,连接PE,根据正方形的性质得到∠A=90°,AD//BC,AB=AD=BC=6,根据全等三角形的性质得到PD=CF=3 2,根据勾股定理和三角形的中位线定理即可得到结论.
本题考查了正方形的性质,全等三角形的判定和性质,解题的关键是掌握正方形的性质,全等三角形的判定和性质.
17.【答案】解:(1)(π−3.14)0−|1− 2|−(12)−2+3−8
=1−( 2−1)−4+(−2)
=1− 2+1−4−2
=−4− 2;
(2)不等式组为:2x+3<1①−2x>6②,
解不等式①,得x<−1,
解不等式②,得x<−3,
所以不等式组的解集是x<−3.
【解析】(1)先根据零指数幂,绝对值,负整数指数幂和立方根进行计算,再算加减即可;
(2)先组成不等式组,再根据不等式的性质求出不等式的解集,再根据求不等式组解集的规律求出不等式组的解集即可.
本题考查了解一元一次不等式组,实数的混合运算,零指数幂,负整数指数幂等知识点,能正确根据实数的运算法则进行计算是解(1)的关键,能根据求不等式组解集的规律求出不等式组的解集是解(2)的关键.
18.【答案】二
【解析】解:(1)小明的解答过程在第二步开始出错;
故答案为:二;
(2)原式=(xx2+x−x2+xx2+x)÷x2−1x2+2x+1
=x−x2−xx(x+1)×x2+2x+1x2−1
=−xx+1×(x+1)2(x+1)(x−1)
=−xx−1.
(1)直接利用分式的混合运算法则判断得出答案;
(2)直接利用分式的混合运算法则化简,进而得出答案.
此题主要考查了分式的混合运算,正确掌握相关运算法则是解题关键.
19.【答案】(1)证明:∵EF//DG,FG//AD,
∴四边形DEFG是平行四边形,
∵BG平分∠ABC,
∴∠ABE=∠CBE,
∵EF//DG,FG//AD,
∴∠ABE=∠DGE,∠DEG=∠EBC,
∴∠DEG=∠DGE,
∴DE=DG,
∴平行四边形DEFG是菱形;
(2)解:∵点E是BG的中点,
∴BE=EG=12BG,
∵AD//BC,
∴△DEG∽△GBC,
∴GEBG=DEBC=12,
∴DE=12BC=3cm,
∵∠ABC=120°,
∴∠DGE=60°,
又∵DE=DG,
∴△DEG是等边三角形,
∴S△DEG= 34DE2=9 34cm2,
∴菱形DEFG的面积=9 32cm2.
【解析】(1)先证四边形DEFG是平行四边形,由平行线的性质和角平分线的性质可得DE=DG,即可求解;
(2)由相似三角形的性质可求DE=3cm,由题意可证△DEG是等边三角形,即可求解.
本题考查了菱形的判定和性质,相似三角形的判定和性质,等边三角形的判定和性质,灵活运用这些解决问题是解题的关键.
20.【答案】54
【解析】解:(1)抽取的学生人数为:4020%=200(人),
∴最喜欢语文学科的学生有:200×22%=44(人),
∴最喜欢化学学科的学生有:200−(44+40+30+15+28)=200−157=43(人),
补全条形图如下:
英语学科所占扇形的圆心角是:30200×360°=54°,
故答案为:54;
(2)1200×15200=90(人),
答:估计最喜欢物理学科的学生约有90人;
(3)画树状图如下:
共有12种等可能的结果数,其中刚好抽到1名男生和1名女生的可能性有6种.
∴刚好抽到1名男生和1名女生的概率为612=12.
(1)由喜欢数学的学生人数除以所占百分比得出抽取的学生人数,即可解决问题;
(2)由该学校学生人数乘以最喜欢物理学科的学生人数所占的比例即可;
(3)画树状图,共有12种等可能的结果数,其中刚好抽到1名男生和1名女生的可能性有6种.再由概率公式求解即可.
本题考查了树状图法求概率以及扇形统计图和条形统计图等知识,树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
21.【答案】解:(1)设该超市购进甲种饮料x箱,乙种饮料y箱,
根据题意得:x+y=50024x+26y=12800,
解得:x=100y=400.
答:该超市购进甲种饮料100箱,乙种饮料400箱;
(2)(29−24)×100+(32−26)×400
=5×100+6×400
=500+2400
=2900(元).
答:该超市共获得利润2900元.
【解析】(1)设该超市购进甲种饮料x箱,乙种饮料y箱,利用总进价=进货单价×进货数量,结合该超市投入12800元的资金购进甲、乙两种饮料共500箱,可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)利用总利润=每箱的销售利润×销售数量(进货数量),即可求出结论.
本题考查了二元一次方程组的应用以及有理数的混合运算,找准等量关系,正确列出二元一次方程组是解题的关键.
22.【答案】(1)证明:∵△ABC和△CDE是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACE=∠BCD,
∴△ACE≌△BCD(SAS),
∴BD=AE;
(2)解:∵△ACE≌△BCD,
∴∠CBD=∠CAE,
∵∠AFB=∠AEC+∠CBD,
∴∠AFB=∠AEC+∠CAE=∠ACB=60°;
(3)证明:如图,过点C作CH⊥AE于H,CN⊥BD于N,
∵△ACE≌△BCD,
∴S△ACE=S△BCD,
∴12×AE⋅CH=12×BD⋅CN,
∴CH=CN,
又∵CH⊥AE,CN⊥BD,
∴FC平分∠EFB.
【解析】(1)“SAS”可证△ACE≌△BCD,可得BD=AE;
(2)由全等三角形的性质可得∠CBD=∠CAE,由外角的性质可求解;
(3)由面积法可证CH=CN,由角平分线的判定定理可得结论.
本题是三角形综合题,考查了全等三角形的判定和性质,等边三角形的性质,证明三角形全等是解题的关键.
23.【答案】解:过点E作EM⊥FG,垂足为M,延长EM交BC于点N,
由题意得:EN⊥BC,HB=MN,EN=20米,
∵HG//BC,
∴∠EGF=∠ECB=30°,
设FM=x米,
∵FG=20米,
∴GM=FG−FM=(20−x)米,
在Rt△EFM中,∠EFG=25°,
∴EM=FM⋅tan25°≈0.47x(米),
在Rt△EMG中,EM=MG⋅tan30°= 33(20−x)m,
∴0.47x= 33(20−x),
解得:x≈11.1,
∴EM=0.47x≈5.2(m),
∴HB=MN=EN−EM=20−5.2=14.8(米),
在Rt△AHF中,∠AFH=45°,AF=40米,
∴AH=AF⋅sin45°=40× 22=20 2(米),
∴AB=AH+BH=20 2+14.8≈43(米),
∴此彩虹滑道最高点A距地面BD的距离约为43米.
【解析】过点E作EM⊥FG,垂足为M,延长EM交BC于点N,根据题意可得:EN⊥BC,HB=MN,EN=20米,根据平行线的性质可得∠EGF=∠ECB=30°,然后设FM=x米,则GM=FG−FM=(20−x)米,在Rt△EFM中,利用锐角三角函数的定义求出EM的长,再在Rt△EMG中,利用锐角三角函数的定义求出EM的长,从而列出关于x的方程,进行计算可求出EM的长,最后利用线段的和差关系可求出MN的长,再在Rt△AHF中,利用锐角三角函数的定义求出AH的长,从而利用线段的和差关系进行计算,即可解答.
本题考查了解直角三角形的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
24.【答案】(1)解:按题意画图如下:
(2)证明:连接OE,OB,
∵四边形ABCD是正方形,
∴AB=BC,∠BCD=90°,
∵BA=BE,
∴BE=BC,
又∵OE=OC,OB=OB,
∴△BEO≌△BCO(SSS),
∴∠BEO=∠BCO=90°,
∴BE⊥OE,
又∵OE为半径,
∴BE为⊙O的切线;
(3)解:连接CE,交OB于点M,
∵BC=BE,OE=OC,
∴OB垂直平分CE,
∴OB⊥CE,EM=CE,
∵OC=2,
∴BC=2OC=4,
∴OB= OC2+BC2= 22+42=2 5,
∵S△BOC=12BO⋅CM=12BC⋅OC,
∴CM=BC⋅OCOB=4×22 5=45 5,
∴CE=2CM=85 5.
【解析】(1)根据题意画出图形即可;
(2)连接OE,OB,由正方形的性质得出AB=BC,∠BCD=90°,证明△BEO≌△BCO(SSS),由全等三角形的得出∠BEO=∠BCO=90°,由切线的判定可得出结论;
(3)连接CE,交OB于点M,证出OB⊥CE,EM=CE,由勾股定理求出OB的长,根据三角形面积可求出CM的长,则可得出答案.
本题考查了切线的判定,正方形的性质,全等三角形的判定与性质,勾股定理,熟练掌握切线的判定是解题的关键.
25.【答案】解:(1)令x=0,则y=4,
∴C(0,4).
令y=0,则x=4,
∴B(4,0).
∵二次函数y=ax2+bx+c图象经过A,B,C三点且A(−1,0),
∴a−b+c=0c=416a+4b+c=0,
解得:a=−1b=3c=4,
∴二次函数的解析式为y=−x2+3x+4;
(2)在抛物线的对称轴上存在点P使得PA+PC的长度最短.点P的坐标为(32,52),理由:
∵y=−x2+3x+4=−(x−32)2+254,
∴抛物线y=−x2+3x+4的对称轴为直线x=32.
设抛物线的对称轴与直线BC交于点P,
∵直线x=32为AB的垂直平分线,
∴PA=PB,
∴PA+PC=PB+PC=BC,
∴此时点P使得PA+PC的长度最短.
令x=32,则y=−32+4=52.
∴在抛物线的对称轴上存在点P使得PA+PC的长度最短,点P的坐标为(32,52);
(3)在直线上方抛物线上存在点Q,使得△QBC的面积有最大值.点Q的坐标为(2,6),此时△QBC的面积为8,理由:
过点Q作QD//y轴,交直线BC于点D,如图,
设点Q(m,−m2+3m+4),则D(m,−m+4),
∴QD=−m2+3m+4−(−m+4)=−m2+4m.
∵B(4,0),
∴OB=4.
∴△QBC的面积=S△QCD+S△QBD
=12×QD⋅OB
=12×4(−m2+4m)
=−2m2+8m
=−2(m−2)2+8.
∵−2<0,
∴当m=2时,△QBC的面积有最大值8,此时点Q的坐标为(2,6).
∴在直线上方抛物线上存在点Q,使得△QBC的面积有最大值.点Q的坐标为(2,6),此时△QBC的面积为8.
【解析】(1)利用待定系数法解答即可;
(2)利用将军饮马模型解答即可;
(3)过点Q作QD//y轴,交直线BC于点D,设点Q(m,−m2+3m+4),则D(m,−m+4),利用△QBC的面积=S△QCD+S△QBD,求出△QBC的面积关于m的函数关系式,再利用配方法和二次函数的性质解答即可得出结论.
本题主要考查了二次函数的图象与性质,抛物线上点的坐标的特征,待定系数法,配方法,函数的极值,理由点的坐标表示出相应线段的长度是解题的关键.
类别/单价
成本
售价
甲
24元/箱
29元/箱
乙
26元/箱
32元/箱
2023年贵州省遵义市仁怀市中考数学第二次适应性试卷(含解析): 这是一份2023年贵州省遵义市仁怀市中考数学第二次适应性试卷(含解析),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年贵州省遵义市仁怀市中考数学第二次适应性试卷(含解析): 这是一份2023年贵州省遵义市仁怀市中考数学第二次适应性试卷(含解析),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年贵州省仁怀市中考第一次适应性考试数学试卷: 这是一份2023年贵州省仁怀市中考第一次适应性考试数学试卷,共6页。