

所属成套资源:历届山东中考数学真题及答案
- _2022年山东威海中考数学试题及答案 试卷 0 次下载
- _2022年山东泰安中考数学试题及答案 试卷 0 次下载
- _2022年山东济南中考数学试题级答案 试卷 0 次下载
- _2022年山东滨州中考数学试题及答案 试卷 0 次下载
- _2021年山东省泰安市中考数学真题及答案 试卷 0 次下载
_2022年山东济宁中考数学试题及答案
展开这是一份_2022年山东济宁中考数学试题及答案,共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022年山东济宁中考数学试题及答案
一、选择题
1. 用四舍五入法取近似值,将数0.0158精确到0.001的结果是( )
A. 0.015 B. 0.016 C. 0.01 D. 0.02
【答案】B
【解析】
【分析】利用四舍五入的方法,从万分位开始四舍五入取近似值即可.
【详解】解:0.0158≈0.016.
故选:B.
【点睛】本题主要考查了近似数和有效数字,正确利用四舍五入法取近似值是解题的关键.
2. 如图是由6个完全相同的小正方体搭建而成的几何体,则这个几何体的主视图是( )
A. B. C. D.
【答案】A
【解析】
【分析】找到从正面看所得的图形即可.
【详解】解:从正面看,底层有3个正方形,第二层有2个正方形,第三层有1个正方形,
故选:A.
【点睛】本题考查简单组合体三视图的识别,主视图是指从物体的正面看物体所得到的图形.
3. 下列各式运算正确的是( )
A. B.
C. D.
【答案】C
【解析】
【分析】利用去括号的法则,幂的运算法则和零指数幂的意义对每个选项进行判断即可.
【详解】A:,故选项A不正确;
B:,故选项B不正确;
C:,故选项C正确;
D:,故选项D不正确;
故选:C.
【点睛】本题考查了去括号法则,幂的运算法则和零指数幂的意义,正确利用上述法则对每个选项做出判断是解题的关键.
4. 下面各式从左到右的变形,属于因式分解的是( )
A. B.
C. D.
【答案】C
【解析】
【分析】根据因式分解的定义对选项逐一分析即可.
【详解】把一个多项式化成几个整式积的形式,这种变形叫做因式分解.
A、右边不是整式积的形式,故不是因式分解,不符合题意;
B、形式上符合因式分解,但等号左右不是恒等变形,等号不成立,不符合题意;
C、符合因式分解的形式,符合题意;
D、从左到右是整式的乘法,从右到左是因式分解,不符合题意;
故选C.
【点睛】本题考查因式分解,解决本题的关键是充分理解并应用因式分解的定义.
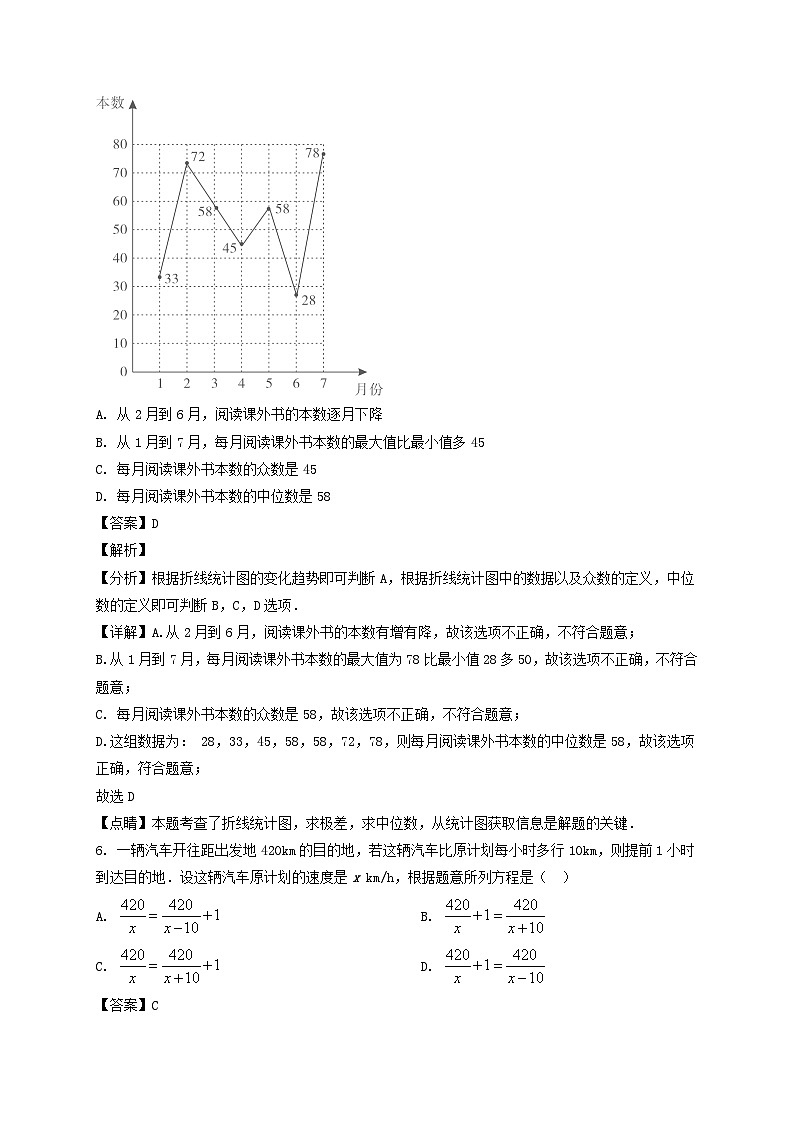
5. 某班级开展“共建书香校园”读书活动.统计了1至7月份该班同学每月阅读课外书的本数,并绘制出如图所示的折线统计图.则下列说法正确的是( )
A. 从2月到6月,阅读课外书的本数逐月下降
B. 从1月到7月,每月阅读课外书本数的最大值比最小值多45
C. 每月阅读课外书本数的众数是45
D. 每月阅读课外书本数的中位数是58
【答案】D
【解析】
【分析】根据折线统计图的变化趋势即可判断A,根据折线统计图中的数据以及众数的定义,中位数的定义即可判断B,C,D选项.
【详解】A.从2月到6月,阅读课外书的本数有增有降,故该选项不正确,不符合题意;
B.从1月到7月,每月阅读课外书本数的最大值为78比最小值28多50,故该选项不正确,不符合题意;
C. 每月阅读课外书本数的众数是58,故该选项不正确,不符合题意;
D.这组数据为: 28,33,45,58,58,72,78,则每月阅读课外书本数的中位数是58,故该选项正确,符合题意;
故选D
【点睛】本题考查了折线统计图,求极差,求中位数,从统计图获取信息是解题的关键.
6. 一辆汽车开往距出发地420km的目的地,若这辆汽车比原计划每小时多行10km,则提前1小时到达目的地.设这辆汽车原计划的速度是x km/h,根据题意所列方程是( )
A. B.
C. D.
【答案】C
【解析】
【分析】设这辆汽车原计划的速度是x km/h,,则实际速度为km/h,根据题意“提前1小时到达目的地”,列分式方程即可求解.
【详解】解:设这辆汽车原计划的速度是x km/h,则实际速度为km/h,
根据题意所列方程是
故选C
【点睛】本题考查了列分式方程,理解题意列出方程是解题的关键.
7. 已知圆锥的母线长8cm,底面圆的直径6cm,则这个圆锥的侧面积是( )
A. 96πcm2 B. 48πcm2 C. 33πcm2 D. 24πcm2
【答案】D
【解析】
【分析】根据圆锥的侧面积=×底面周长×母线长计算即可求解.
【详解】解:底面直径为6cm,则底面周长=6π,
侧面面积=×6π×8=24πcm2.
故选D.
【点睛】本题考查圆锥的计算,解题的关键是熟练掌握圆锥的侧面积=×底面周长×母线长.
8. 若关于x的不等式组仅有3个整数解,则a的取值范围是( )
A. -4≤a<-2 B. -3<a≤-2
C. -3≤a≤-2 D. -3≤a<-2
【答案】D
【解析】
【分析】先求出每个不等式的解集,再求出不等式组的解集,即可解答.
详解】解:
由①得,
由②得,
因不等式组有3个整数解
故选:D.
【点睛】本题考查解一元一次不等式组、一元一次不等式组的整数解,掌握相关知识是解题关键.
9. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( )
A. B. C. D.
【答案】A
【解析】
【分析】根据题意可得AD = AB = 2, ∠B = ∠ADB, CE= DE, ∠C=∠CDE,可得∠ADE = 90°,继而设AE=x,则CE=DE=3-x,根据勾股定理即可求解.
【详解】解:∵沿过点A的直线将纸片折叠,使点B落在边BC上的点D处,
∴AD = AB = 2, ∠B = ∠ADB,
∵折叠纸片,使点C与点D重合,
∴CE= DE, ∠C=∠CDE,
∵∠BAC = 90°,
∴∠B+ ∠C= 90°,
∴∠ADB + ∠CDE = 90°,
∴∠ADE = 90°,
∴AD2 + DE2 = AE2,
设AE=x,则CE=DE=3-x,
∴22+(3-x)2 =x2,
解得
即AE=
故选A
【点睛】本题考查了折叠的性质,勾股定理,掌握折叠的性质以及勾股定理是解题的关键.
10. 如图,用相同的圆点按照一定的规律拼出图形.第一幅图4个圆点,第二幅图7个圆点,第三幅图10个圆点,第四幅图13个圆点……按照此规律,第一百幅图中圆点的个数是( )
A. 297 B. 301 C. 303 D. 400
【答案】B
【解析】
【分析】首先根据前几个图形圆点的个数规律即可发现规律,从而得到第100个图摆放圆点的个数.
【详解】解:观察图形可知:第1幅图案需要4个圆点,即4+3×0,
第2幅图7个圆点,即4+3=4+3×1;
第3幅图10个圆点,即4+3+3=4+3×2;
第4幅图13个圆点,即4+3+3+3=4+3×3;
第n幅图中,圆点的个数为:4+3(n-1)=3n+1,
……,
第100幅图,圆中点的个数为:3×100+1=301.
故选:B.
【点睛】本题主要考查了图形的变化规律,解答的关键是由所给的图形总结出存在的规律.
二、填空题
11. 若二次根式有意义,则x的取值范围是________.
【答案】
【解析】
【分析】根据二次根式的被开方数是非负数列出不等式,解不等式即可.
【详解】根据题意,得,
解得:;
故答案为:.
【点睛】本题考查的是二次根式有意义的条件,掌握二次根式的被开方数是非负数是解题的关键.
12. 如图,直线l1,l2,l3被直线l4所截,若l1l2,l2l3,∠1=126o32',则∠2的度数是___________.
【答案】
【解析】
【分析】根据平行线的性质得,根据等量等量代换得,进而根据邻补角性质即可求解.
【详解】解:如图
l1l2,l2l3,
,,
,
∠1=,
,
故答案为:.
【点睛】本题考查了邻补角,平行线的性质,掌握平行线的性质是解题的关键.
13. 已知直线y1=x-1与y2=kx+b相交于点(2,1).请写出b值____(写出一个即可),使x>2时,y1>y2.
【答案】2(答案不唯一)
【解析】
【分析】根据题意将点(2,1)代入y2=kx+b可得,即,根据x>2时,y1>y2,可得,即可求得的范围,即可求解.
【详解】解:∵直线y1=x-1与y2=kx+b相交于点(2,1),
∴点(2,1)代入y2=kx+b,
得,
解得,
∵直线y1=x-1,随的增大而增大,
又 x>2时,y1>y2,
,
,
解得,
故答案为:2(答案不唯一)
【点睛】本题考查了两直线交点问题,掌握一次函数的性质是解题的关键.
14. 如图,A是双曲线上的一点,点C是OA的中点,过点C作y轴的垂线,垂足为D,交双曲线于点B,则△ABD的面积是___________.
【答案】4
【解析】
【分析】根据点C是OA的中点,根据三角形中线的可得S△ACD = S△OCD, S△ACB = S△OCB,进而可得S△ABD = S△OBD,根据点B在双曲线上,BD⊥ y轴,可得S△OBD=4,进而即可求解.
【详解】点C是OA的中点,
∴S△ACD = S△OCD, S△ACB = S△OCB,
∴S△ACD + S△ACB = S△OCD + S△OCB,
∴S△ABD = S△OBD,
点B在双曲线上,BD⊥ y轴,
∴S△OBD=×8=4,
∴S△ABD =4,
答案为:4.
【点睛】本题考查了三角形中线的性质,反比例函数的的几何意义,掌握反比例函数的几何意义是解题的关键.
15. 如图,点A,C,D,B在⊙O上,AC=BC,∠ACB=90°.若CD=a,tan∠CBD=,则AD的长是___________.
【答案】
【解析】
【分析】如图,连接,设交于点,根据题意可得是的直径,,设,证明,根据相似三角形的性质以及正切的定义,分别表示出,根据,勾股定理求得,根据即可求解.
【详解】解:如图,连接,设交于点,
∵∠ACB=90°
∴是的直径,
,
tan∠CBD=,
,
在中, ,
,
,
,
设
则,
AC=BC,
,
,
中,,
,
,
,
又,
,
,
,
,
,
,
,
解得,
,
故答案为:.
【点睛】本题考查了90°圆周角所对的弦是直径,同弧所对的圆周角相等,正切的定义,相似三角形的性质与判定,勾股定理,掌握以上知识是解题的关键.
三、解答题
16. 已知,,求代数式的值.
【答案】-4
【解析】
分析】先将代数式因式分解,再代入求值.
【详解】
故代数式的值为.
【点睛】本题考查因式分解、二次根式的混合运算,解决本题的关键是熟练进行二次根式的计算.
17. 6月5日是世界环境日.某校举行了环保知识竞赛,从全校学生中随机抽取了n名学生的成绩进行分析,并依据分析结果绘制了不完整的统计表和统计图(如下图所示).
学生成绩分布统计表
成绩/分
组中值
频率
75.5≤x<80.5
78
0.05
80.5≤x<85.5
83
a
85.5≤x<90.5
88
0.375
90.5≤x<95.5
93
0.275
95.5≤x<100.5
98
0.05
请根据以上图表信息,解答下列问题:
(1)填空:n= ,a= ;
(2)请补全频数分布直方图;
(3)求这n名学生成绩的平均分;
(4)从成绩在75.5≤x<80.5和95.5≤x<100.5的学生中任选两名学生.请用列表法或画树状图的方法,求选取的学生成绩在75.5≤x<80.5和95.5≤x<100.5中各一名的概率.
【答案】(1)40,0.25
(2)见解析 (3)88.125分
(4)图表见解析,
【解析】
【分析】(1)根据“频率=频数÷总数”和频率之和为1可得答案;
(2)用总人数减去其他组的人数即为到组人数,即可补全频数分布直方图;
(3)利用平均数的计算公式计算即可;
(4)列出树状图即可求出概率
【小问1详解】
解:由图表可知:,
【小问2详解】
解:由(1)可知,到组人数为(人),
频数分布图为:
【小问3详解】
解: (分)
【小问4详解】
解:解:用A1,A2表示75.5≤x<80.5中的两名学生,用B1,B2表示95.5≤x<100.5中的两名学生,画树状图,得
由上图可知,所有结果可能性共12种,而每一种结果的可能性是一样的,其中每一组各有一名学生被选到有8种.
∴每一组各有一名学生被选到的概率为.
【点睛】本题主要考查本题考查读频数分布直方图,求平均数,利用树状图求概率,掌握相关的概念以及方法是解题的关键.
18. 如图,在矩形ABCD中,以AB的中点O为圆心,以OA为半径作半圆,连接OD交半圆于点E,在上取点F,使,连接BF,DF.
(1)求证:DF与半圆相切;
(2)如果AB=10,BF=6,求矩形ABCD的面积.
【答案】(1)见解析 (2)
【解析】
【分析】(1)连接OF,证明,可得,根据矩形的性质可得,进而即可得证;
(2)连接,根据题意证明,根据相似三角形的性质求得,进而勾股定理,根据矩形的面积公式即可求解.
【小问1详解】
证明:连接OF.
,
,
四边形是矩形,
【小问2详解】
解:连接,
,,
,
为半圆的直径,
,
,
,
,
,
,
在中,
矩形的面积为
【点睛】本题考查了切线的性质,相似三角形的性质与判定,勾股定理,矩形的性质,掌握以上知识是解题的关键.
19. 某运输公司安排甲、乙两种货车24辆恰好一次性将328吨的物资运往A,B两地,两种货车载重量及到A,B两地的运输成本如下表:
货车类型
载重量(吨/辆)
运往A地的成本(元/辆)
运往B地的成本(元/辆)
甲种
16
1200
900
乙种
12
1000
750
(1)求甲、乙两种货车各用了多少辆;
(2)如果前往A地的甲、乙两种货车共12辆,所运物资不少于160吨,其余货车将剩余物资运往B地.设甲、乙两种货车到A,B两地的总运输成本为w元,前往A地的甲种货车为t辆.
①写出w与t之间的函数解析式;
②当t为何值时,w最小?最小值是多少?
【答案】(1)甲种货车用10辆,则乙种货车用14辆
(2)①;②t=4时,w最小=22 700元
【解析】
【分析】(1)设甲种货车用x辆,则乙种货车用(24-x)辆.根据题意列一元一次方程即可求解;
(2)①根据表格信息列出w与t之间的函数解析式;
②根据所运物资不少于160吨列出不等式,求得的范围,然后根据一次函数的性质求得最小值即可.
【小问1详解】
(1)设甲种货车用x辆,则乙种货车用(24-x)辆.根据题意,得
16x+12(24-x)=328.
解得x=10.
∴24-x=24-10=14.
答:甲种货车用10辆,则乙种货车用14辆.
【小问2详解】
①.
②
∵50>0,
∴w随t的减小而减小.
∴当t=4时,w最小=50×4+22 500=22 700(元).
【点睛】本题考查了一元一次方程的应用,一元一次不等式的应用,一次函数的应用,根据题意列出方程,不等式与一次函数关系式是解题的关键.
20. 知识再现:如图1,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
∵,
∴,
∴
(1)拓展探究:如图2,在锐角ABC中,∠A,∠B,∠C的对边分别为a,b,c.请探究,,之间的关系,并写出探究过程.
(2)解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.
【答案】(1),证明见解析
(2)米
【解析】
【分析】拓展研究:作CD⊥AB于点D,AE⊥BC于点E,根据正弦的定义得AE = csinB,
AE= bsin∠BCA,CD= asinB,CD = bsin∠BAC,从而得出结论;
解决问题:由拓展探究知, 代入计算即可.
【小问1详解】
(拓展探究)证明:作CD⊥AB于点D,AC⊥BC于点E.
在RtΔABE中,,
同理:,
.
.
.
.
.
【小问2详解】
(解答问题)解:在ΔABC中,
∴
解得:
答:点A到点B的距离为m.
【点睛】本题主要考查了解直角三角形,对于锐角三角形,利用正弦的定义,得出是解题的关键.
21. 已知抛物线与x轴有公共点.
(1)当y随x的增大而增大时,求自变量x的取值范围;
(2)将抛物线先向上平移4个单位长度,再向右平移n个单位长度得到抛物线(如图所示),抛物线与x轴交于点A,B(点A在点B的右侧),与y轴交于点C.当OC=OA时,求n的值;
(3)D为抛物线的顶点,过点C作抛物线的对称轴l的垂线,垂足为G,交抛物线于点E,连接BE交l于点F.求证:四边形CDEF是正方形.
【答案】(1)
(2)n=2 (3)见解析
【解析】
【分析】(1)根据抛物线与轴由公共点,可得,从而而求出的值,进而求得抛物线对称轴,进一步得到结果;
(2)根据图像平移的特征可求出平移后抛物线的解析式,根据和分别得出点和的坐标,根据列出方程,进而求的结果;
(3)从而得出点、点的坐标,由抛物线的解析式可得出点的坐标和点的坐标,进而求得的解析式,从而得出点的坐标,进而得出,进一步得出结论.
【小问1详解】
解:∵抛物线与x轴有公共点,
∴
∴∴.
∴,
∴,
∵,
∴当时,y随着x的增大而增大.
【小问2详解】
解:由题意,得,
当y=0时,,
解得:或,
∵点A在点B的右侧,
∴点A的坐标为(1+n,0),点B的坐标为(-3+n,0).
∵点C的坐标为(0,-n2 +2n+3),
∴n+1=-n2+2n+3.
解得:n=2或n=-1(舍去).
故n的值为2.
【小问3详解】
解:由(2)可知:抛物线C2的解析式为y=-(x-1)2+4.
∴点A的坐标为(3,0),点B的坐标为(-1,0)
点C的坐标为(0,3),点D的坐标为(1,4),
抛物线C2的对称轴是直线x=1,
∵点E与点C关于直线x=1对称,
∴点E的坐标为(2,3).
∴点G的坐标为(1,3).
设直线BE解析式为y=kx+b,
∴
解得:
∴y=x+1.
当x=1时,y=1+1=2.点F的坐标为(1,2).
∴FG=EG=DG=CG=1.
∴四边形CDEF为矩形.
又∵CE⊥DF,
∴四边形CDEF为正方形.
【点睛】本题主要考查二次函数的图像与性质,求一次函数的解析式,平移图像的特征,正方形的判定,解决问题的关键是平移前后抛物线解析式之间的关系.
22. 如图,△AOB是等边三角形,过点A作y轴的垂线,垂足为C,点C的坐标为(0,).P是直线AB上在第一象限内的一动点,过点P作y轴的垂线,垂足为D,交AO于点E,连接AD,作DM⊥AD交x轴于点M,交AO于点F,连接BE,BF.
(1)填空:若△AOD是等腰三角形,则点D的坐标为 ;
(2)当点P在线段AB上运动时(点P不与点A,B重合),设点M的横坐标为m.
①求m值最大时点D的坐标;
②是否存在这样m值,使BE=BF?若存在,求出此时的m值;若不存在,请说明理由.
【答案】(1)或
(2)①点D坐标;②存在,
【解析】
【分析】(1)根据题意易得∠AOB=60°从而∠AOC=30°和∠CDA=60°,根据tan30°求得AC的长,再根据sin60°求得AD的长,当OA=AD和OD=OA时分情况讨论,即可得到OD的长,从而得到D点坐标;
(2)①设点D的坐标为(0,a),则OD=a,CD=-a,易证,从而得出,代入即可得到m与a的函数关系,化为顶点式即可得出答案;
②作FH⊥y轴于点H,得到AC∥PD∥FH∥x轴,易得,,易证得出,即,设,则,通过证得得出,代入即可得到n的值,进一步得到m的值.
【小问1详解】
∵△AOB是等边三角形,
∴∠AOB=60°,∴∠AOC=30°,
∵AC⊥y轴,点C的坐标为(0,),
∴OC=,
∴,
当△AOD是等腰三角形,OD=AD,∠DAO=∠DOA=30°,
∴∠CDA=60°,
∴,
∴,
∴D的坐标为,
当△AOD是等腰三角形,此时OA=OD时,,
∴OD=OA=2,
∴点D坐标为(0,2),
故答案为:或(0,2);
【小问2详解】
①解:设点D的坐标为(0,a),则OD=a,CD=-a,
∵△AOB是等边三角形,
∴,
∴,
在RtΔAOC中,,
∴,
∴,
∵,∴,
∵,∴,
∵,
∴,
∴,即:,
∴,
∴当时,m的最大值为;
∴m的最大值为时,点D坐标为;
②存在这样的m值,使BE=BF;
作FH⊥y轴于点H,
∴AC∥PD∥FH∥x轴,
∴,,
,
,
,,
∴,
∵,
∴,
∴,
∴,
∴,
设,则,
,
∵,,
∴,
∴,
∴,
解得: 或 ,
当时,点P与点A重合,不合题意,舍去,
当时, ,
存在这样m值,使BE=BF.此时 .
【点睛】本题考查了等边三角形的性质、特殊角的三角函数,全等三角形的判定和性质、相似三角形的判定和性质以及二次函数的综合运用,解题的关键是得出二次函数的关系式,是对知识的综合考查.
相关试卷
这是一份_2023年山东济宁中考数学试题及答案,共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023年山东省济宁市中考数学试题(图片版),共7页。
这是一份2023年山东省济宁市中考冲刺模拟+数学试题,共10页。












