







浙江省温州市2021-2023三年中考数学真题分类汇编
展开浙江省温州市2021-2023三年中考数学真题分类汇编-02填空题知识点分类
一.因式分解-提公因式法(共1小题)
1.(2023•温州)分解因式:2a2﹣2a= .
二.因式分解-运用公式法(共1小题)
2.(2022•温州)分解因式:m2﹣n2= .
三.提公因式法与公式法的综合运用(共1小题)
3.(2021•温州)分解因式:2m2﹣18= .
四.分式的加减法(共1小题)
4.(2022•温州)计算:+= .
五.解一元一次不等式组(共2小题)
5.(2023•温州)不等式组的解是 .
6.(2021•温州)不等式组的解集为 .
六.反比例函数的应用(共1小题)
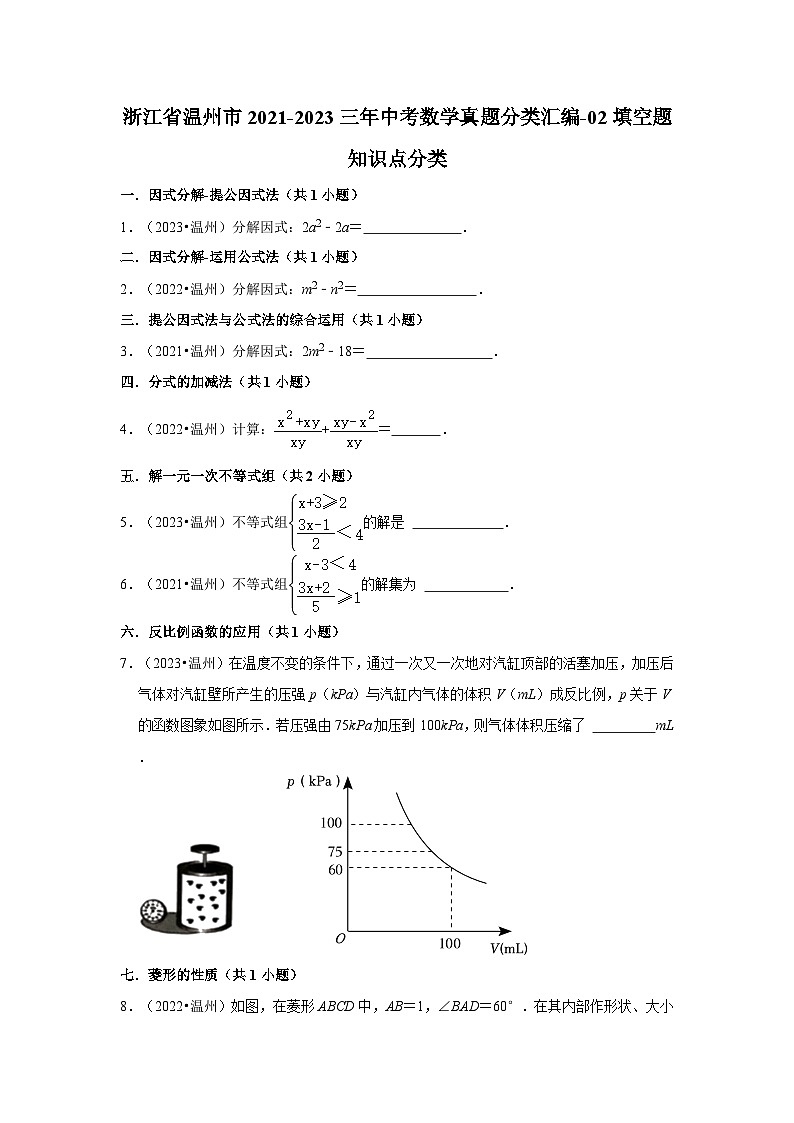
7.(2023•温州)在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,加压后气体对汽缸壁所产生的压强p(kPa)与汽缸内气体的体积V(mL)成反比例,p关于V的函数图象如图所示.若压强由75kPa加压到100kPa,则气体体积压缩了 mL.
七.菱形的性质(共1小题)
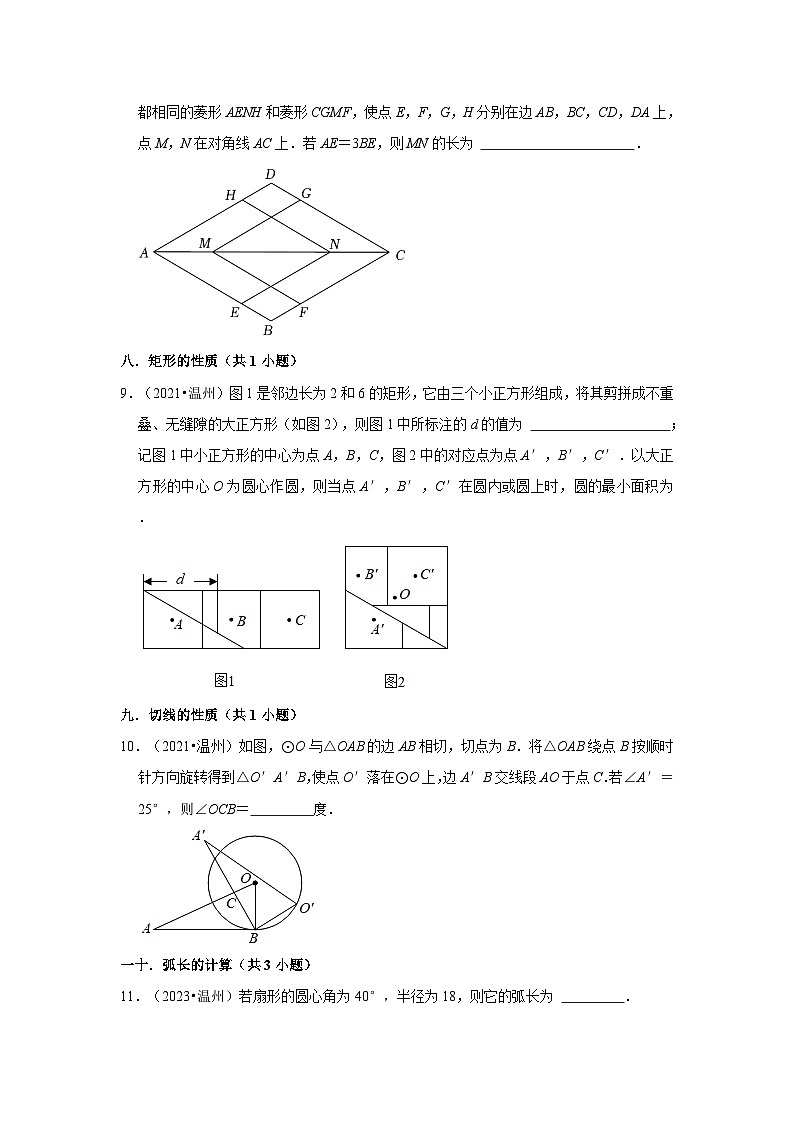
8.(2022•温州)如图,在菱形ABCD中,AB=1,∠BAD=60°.在其内部作形状、大小都相同的菱形AENH和菱形CGMF,使点E,F,G,H分别在边AB,BC,CD,DA上,点M,N在对角线AC上.若AE=3BE,则MN的长为 .
八.矩形的性质(共1小题)
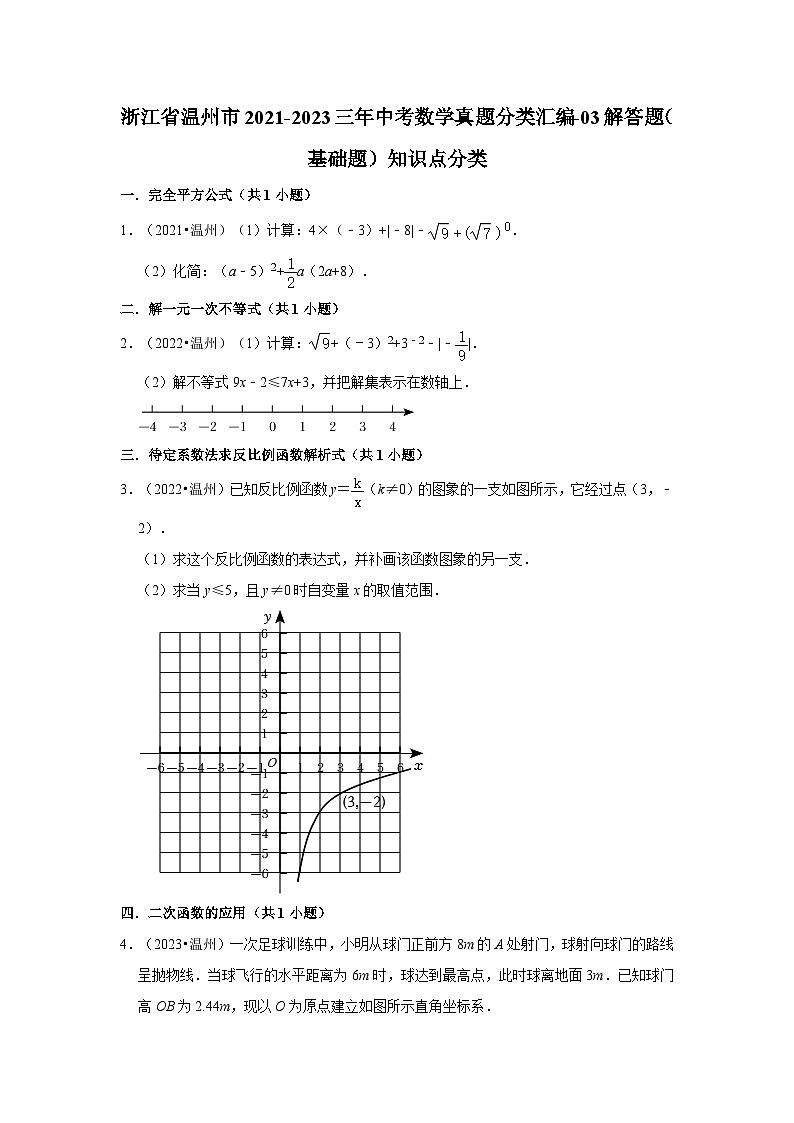
9.(2021•温州)图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图2),则图1中所标注的d的值为 ;记图1中小正方形的中心为点A,B,C,图2中的对应点为点A′,B′,C′.以大正方形的中心O为圆心作圆,则当点A′,B′,C′在圆内或圆上时,圆的最小面积为 .
九.切线的性质(共1小题)
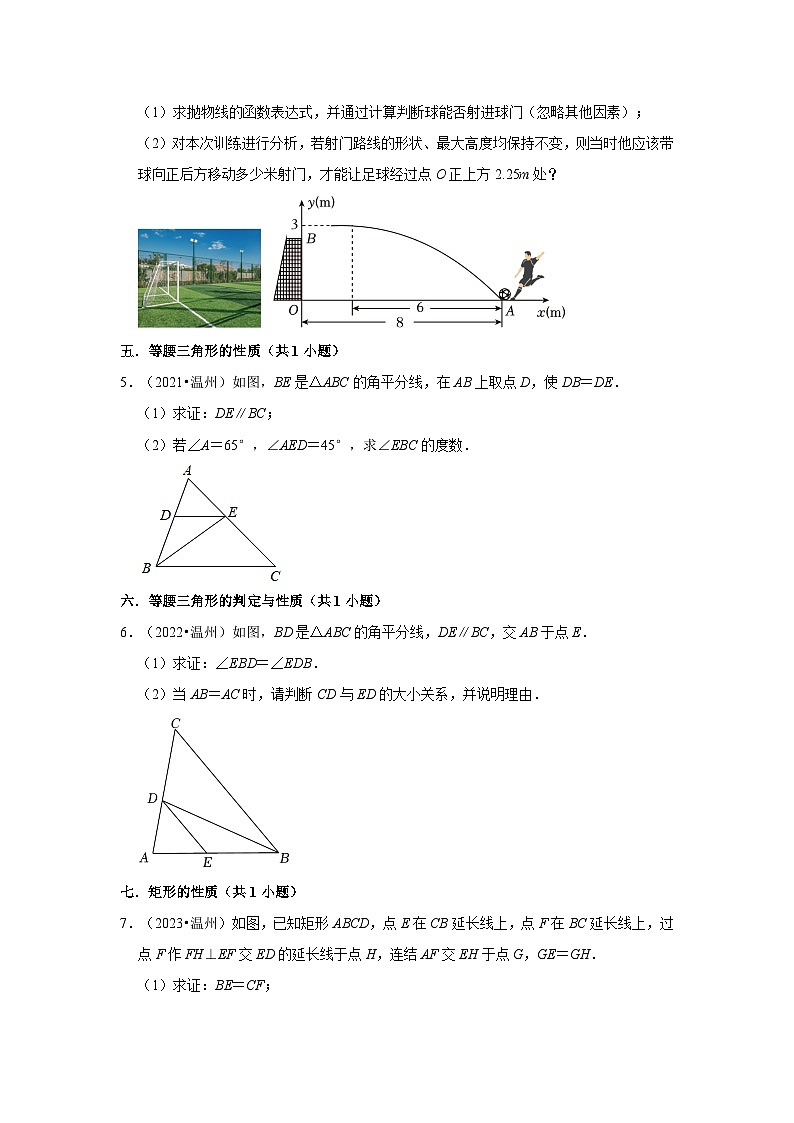
10.(2021•温州)如图,⊙O与△OAB的边AB相切,切点为B.将△OAB绕点B按顺时针方向旋转得到△O′A′B,使点O′落在⊙O上,边A′B交线段AO于点C.若∠A′=25°,则∠OCB= 度.
一十.弧长的计算(共3小题)
11.(2023•温州)若扇形的圆心角为40°,半径为18,则它的弧长为 .
12.(2021•温州)若扇形的圆心角为30°,半径为17,则扇形的弧长为 .
13.(2022•温州)若扇形的圆心角为120°,半径为,则它的弧长为 .
一十一.扇形面积的计算(共1小题)
14.(2023•温州)图1是4×4方格绘成的七巧板图案,每个小方格的边长为,现将它剪拼成一个“房子”造型(如图2),过左侧的三个端点作圆,并在圆内右侧部分留出矩形CDEF作为题字区域(点A,E,D,B在圆上,点C,F在AB上),形成一幅装饰画,则圆的半径为 .若点A,N,M在同一直线上,AB∥PN,DE=EF,则题字区域的面积为 .
一十二.相似三角形的应用(共1小题)
15.(2022•温州)如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片OA,OB,此时各叶片影子在点M右侧成线段CD,测得MC=8.5m,CD=13m,垂直于地面的木棒EF与影子FG的比为2:3,则点O,M之间的距离等于 米.转动时,叶片外端离地面的最大高度等于 米.
一十三.频数(率)分布直方图(共1小题)
16.(2023•温州)某校学生“亚运知识”竞赛成绩的频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩在80分及以上的学生有 人.
一十四.算术平均数(共1小题)
17.(2022•温州)某校5个小组在一次植树活动中植树株数的统计图如图所示,则平均每组植树 株.
一十五.概率公式(共1小题)
18.(2021•温州)一个不透明的袋中装有21个只有颜色不同的球,其中5个红球,7个白球,9个黄球.从中任意摸出1个球是红球的概率为 .
浙江省温州市2021-2023三年中考数学真题分类汇编-02填空题知识点分类
参考答案与试题解析
一.因式分解-提公因式法(共1小题)
1.(2023•温州)分解因式:2a2﹣2a= 2a(a﹣1) .
【答案】2a(a﹣1).
【解答】解:2a2﹣2a=2a(a﹣1).
故答案为:2a(a﹣1).
二.因式分解-运用公式法(共1小题)
2.(2022•温州)分解因式:m2﹣n2= (m+n)(m﹣n) .
【答案】(m+n)(m﹣n).
【解答】解:m2﹣n2=(m+n)(m﹣n),
故答案为:(m+n)(m﹣n).
三.提公因式法与公式法的综合运用(共1小题)
3.(2021•温州)分解因式:2m2﹣18= 2(m+3)(m﹣3) .
【答案】见试题解答内容
【解答】解:原式=2(m2﹣9)
=2(m+3)(m﹣3).
故答案为:2(m+3)(m﹣3).
四.分式的加减法(共1小题)
4.(2022•温州)计算:+= 2 .
【答案】2.
【解答】解:原式=,
=,
=2.
故答案为:2.
五.解一元一次不等式组(共2小题)
5.(2023•温州)不等式组的解是 ﹣1≤x<3 .
【答案】﹣1≤x<3.
【解答】解:,
解不等式①,得:x≥﹣1,
解不等式②,得:x<3,
∴该不等式组的解集为﹣1≤x<3,
故答案为:﹣1≤x<3.
6.(2021•温州)不等式组的解集为 1≤x<7 .
【答案】1≤x<7.
【解答】解:解不等式x﹣3<4,得:x<7,
解不等式≥1,得:x≥1,
则不等式组的解集为1≤x<7,
故答案为:1≤x<7.
六.反比例函数的应用(共1小题)
7.(2023•温州)在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,加压后气体对汽缸壁所产生的压强p(kPa)与汽缸内气体的体积V(mL)成反比例,p关于V的函数图象如图所示.若压强由75kPa加压到100kPa,则气体体积压缩了 20 mL.
【答案】20.
【解答】解:设这个反比例函数的解析式为V=,
∵V=100ml时,p=60kpa,
∴k=PV=100ml×60kpa=6000,
∴V=,
当P=75kPa时,V==80,
当P=100kPa时,V==60,
∴80﹣60=20(mL),
∴气体体积压缩了20mL,
故答案为:20.
七.菱形的性质(共1小题)
8.(2022•温州)如图,在菱形ABCD中,AB=1,∠BAD=60°.在其内部作形状、大小都相同的菱形AENH和菱形CGMF,使点E,F,G,H分别在边AB,BC,CD,DA上,点M,N在对角线AC上.若AE=3BE,则MN的长为 .
【答案】.
【解答】解:方法一:连接DB交AC于点O,作MI⊥AB于点I,作FJ⊥AB交AB的延长线于点J,如图1所示,
∵四边形ABCD是菱形,∠BAD=60°,AB=1,
∴AB=BC=CD=DA=1,∠BAC=30°,AC⊥BD,
∵△ABD是等边三角形,
∴OD=,
∴AO===,
∴AC=2AO=,
∵AE=3BE,
∴AE=,BE=,
∵菱形AENH和菱形CGMF大小相同,
∴BE=BF=,∠FBJ=60°,
∴FJ=BF•sin60°=×=,
∴MI=FJ=,
∴AM===,
同理可得,CN=,
∴MN=AC﹣AM﹣CN=﹣=,
故答案为:.
方法二:连接DB交AC于点O,连接EF,
由题意可得,四边形AMFE是平行四边形,四边形EFCN是平行四边形,
∴EF=AM=CN,
∵EF∥AC,
∴△BEF∽△BAC,
∴,
∵AE=3BE,AB=1,
∴AB=4BE,
∴=,
∴AM=CN=AC,
∴MN=AC=OA,
∵∠BAD=60°.AB=AD=1,AO垂直平分BD,
∴OD=,
∴OA===,
∴MN=,
故答案为:.
八.矩形的性质(共1小题)
9.(2021•温州)图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图2),则图1中所标注的d的值为 6﹣2 ;记图1中小正方形的中心为点A,B,C,图2中的对应点为点A′,B′,C′.以大正方形的中心O为圆心作圆,则当点A′,B′,C′在圆内或圆上时,圆的最小面积为 (16﹣8)π .
【答案】6﹣2,(16﹣8)π.
【解答】解:如图,连接FW,由题意可知点A′,O,C′在线段FW上,连接OB′,B′C′,过点O作OH⊥B′C′于H.
∵大正方形的面积=12,
∴FG=GW=2,
∵EF=WK=2,
∴在Rt△EFG中,tan∠EGF===,
∴∠EGF=30°,
∵JK∥FG,
∴∠KJG=∠EGF=30°,
∴d=JK=GK=(2﹣2)=6﹣2,
∵OF=OW=FW=,C′W=,
∴OC′=﹣,
∵B′C′∥QW,B′C′=2,
∴∠OC′H=∠FWQ=45°,
∴OH=HC′=﹣1,
∴HB′=2﹣(﹣1)=3﹣,
∴OB′2=OH2+B′H2=(﹣1)2+(3﹣)2=16﹣8,
∵OA′=OC′<OB′,
∴当点A′,B′,C′在圆内或圆上时,圆的最小面积为(16﹣8)π.
故答案为:6﹣2,(16﹣8)π.
九.切线的性质(共1小题)
10.(2021•温州)如图,⊙O与△OAB的边AB相切,切点为B.将△OAB绕点B按顺时针方向旋转得到△O′A′B,使点O′落在⊙O上,边A′B交线段AO于点C.若∠A′=25°,则∠OCB= 85 度.
【答案】见试题解答内容
【解答】解:∵⊙O与△OAB的边AB相切,
∴OB⊥AB,
∴∠OBA=90°,
连接OO′,如图,
∵△OAB绕点B按顺时针方向旋转得到△O′A′B,
∴∠A=∠A′=25°,∠ABA′=∠OBO′,BO=BO′,
∵OB=OO′,
∴△OO′B为等边三角形,
∴∠OBO′=60°,
∴∠ABA′=60°,
∴∠OCB=∠A+∠ABC=25°+60°=85°.
故答案为85.
一十.弧长的计算(共3小题)
11.(2023•温州)若扇形的圆心角为40°,半径为18,则它的弧长为 4π .
【答案】4π.
【解答】解:由弧长公式得,
故答案为:4π.
12.(2021•温州)若扇形的圆心角为30°,半径为17,则扇形的弧长为 π .
【答案】π.
【解答】解:根据弧长公式可得:
l===π.
故答案为:π.
13.(2022•温州)若扇形的圆心角为120°,半径为,则它的弧长为 π .
【答案】π.
【解答】解:∵扇形的圆心角为120°,半径为,
∴它的弧长为:=π,
故答案为:π.
一十一.扇形面积的计算(共1小题)
14.(2023•温州)图1是4×4方格绘成的七巧板图案,每个小方格的边长为,现将它剪拼成一个“房子”造型(如图2),过左侧的三个端点作圆,并在圆内右侧部分留出矩形CDEF作为题字区域(点A,E,D,B在圆上,点C,F在AB上),形成一幅装饰画,则圆的半径为 5 .若点A,N,M在同一直线上,AB∥PN,DE=EF,则题字区域的面积为 .
【答案】5;.
【解答】解:如图所示,依题意,GH=2=GQ,
∵过左侧的三个端点Q,K,L作圆,QH=HL=4,
又NK⊥QL,
∴O在KN上,连接OQ,则OQ为半径,
∵OH=r﹣KH=r﹣2,
在Rt△OHQ中,OH2+QH2=QO2,
∴(r﹣2)2+42=r2,
解得:r=5;
连接OE,取ED的中点T,连接OT,交AB于点S,连接PB,AM,
∵AB∥PN,
∴AB⊥OT,
∴AS=SB,
∵点A,N,M在同一直线上,
∴,
∴MN=AN,
又NB=NA,
∴∠ABM=90°,
∵MN=NB,NP⊥MP,
∴MP=PB=2,
∴NS=MB=2,
∵KH+HN=2+4=6,
∴ON=6﹣5=1,
∴OS=3,
∵,
设EF=ST=a,则 ,
在Rt△OET中,OE2=OT2+TE2,即 ,
整理得 5a2+12a﹣32=0,
即(a+4)(5a﹣8)=0,
解得: 或a=﹣4,
∴题字区域的面积为 .
故答案为:.
一十二.相似三角形的应用(共1小题)
15.(2022•温州)如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片OA,OB,此时各叶片影子在点M右侧成线段CD,测得MC=8.5m,CD=13m,垂直于地面的木棒EF与影子FG的比为2:3,则点O,M之间的距离等于 10 米.转动时,叶片外端离地面的最大高度等于 (10+) 米.
【答案】10,(10+).
【解答】解:解法一:如图,过点O作OP∥BD,交MG于P,过P作PN⊥BD于N,则OB=PN,
∵AC∥BD,
∴AC∥OP∥BD,
∴=,∠EGF=∠OPM,
∵OA=OB,
∴CP=PD=CD=6.5,
∴MP=CM+CP=8.5+6.5=15,
tan∠EGF=tan∠OPM,
∴==,
∴OM=×15=10;
∵DB∥EG,
∴∠EGF=∠NDP,
∴sin∠EGF=sin∠NDP,即=,
∴OB=PN=,
以点O为圆心,OA的长为半径作圆,当OB与OM共线时,叶片外端离地面的高度最大,其最大高度等于(10+)米.
解法二:如图,设AC与OM交于点H,过点C作CN⊥BD于N,
∵HC∥EG,
∴∠HCM=∠EGF,
∵∠CMH=∠EFG=90°,
∴△HMC∽△EFG,
∴==,即=,
∴HM=,
∵BD∥EG,
∴∠BDC=∠EGF,
∴tan∠BDC=tan∠EGF,
∴==,
设CN=2x,DN=3x,则CD=x,
∴x=13,
∴x=,
∴AB=CN=2,
∴OA=OB=AB=,
在Rt△AHO中,∵∠AHO=∠CHM,
∴sin∠AHO==,
∴=,
∴OH=,
∴OM=OH+HM=+=10(米),
以点O为圆心,OA的长为半径作圆,当OB与OM共线时,叶片外端离地面的高度最大,其最大高度等于(10+)米.
故答案为:10,(10+).
一十三.频数(率)分布直方图(共1小题)
16.(2023•温州)某校学生“亚运知识”竞赛成绩的频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩在80分及以上的学生有 140 人.
【答案】140.
【解答】解:其中成绩在80分及以上的学生有:80+60=140(人).
故答案为:140.
一十四.算术平均数(共1小题)
17.(2022•温州)某校5个小组在一次植树活动中植树株数的统计图如图所示,则平均每组植树 5 株.
【答案】5.
【解答】解:观察图形可知:=×(4+3+7+4+7)=5,
∴平均每组植树5株.
故答案为:5.
一十五.概率公式(共1小题)
18.(2021•温州)一个不透明的袋中装有21个只有颜色不同的球,其中5个红球,7个白球,9个黄球.从中任意摸出1个球是红球的概率为 .
【答案】.
【解答】解:∵一共有21个只有颜色不同的球,其中红球有5个,
∴从中任意摸出1个球是红球的概率为,
故答案为:.
2021-2023三年浙江省温州市中考数学真题分类汇编-03解答题(提升题)知识点分类(含答案): 这是一份2021-2023三年浙江省温州市中考数学真题分类汇编-03解答题(提升题)知识点分类(含答案),共29页。试卷主要包含了计算,某公司生产的一种营养品信息如表,根据以下素材,探索完成任务,,且∠AEB=∠CFD=90°,,且满足=,,连结AE等内容,欢迎下载使用。
2021-2023三年浙江省绍兴市中考数学真题分类汇编-02填空题知识点分类(含答案): 这是一份2021-2023三年浙江省绍兴市中考数学真题分类汇编-02填空题知识点分类(含答案),共18页。试卷主要包含了因式分解,分解因式,方程的解是 等内容,欢迎下载使用。
浙江省绍兴市2021-2023三年中考数学真题分类汇编: 这是一份浙江省绍兴市2021-2023三年中考数学真题分类汇编,文件包含浙江省绍兴市2021-2023三年中考数学真题分类汇编-03解答题提升题知识点分类doc、浙江省绍兴市2021-2023三年中考数学真题分类汇编-01选择题知识点分类doc、浙江省绍兴市2021-2023三年中考数学真题分类汇编-03解答题基础题知识点分类doc、浙江省绍兴市2021-2023三年中考数学真题分类汇编-02填空题知识点分类doc等4份试卷配套教学资源,其中试卷共90页, 欢迎下载使用。












