北师大版九年级下册2 圆的对称性教课内容ppt课件

这是一份北师大版九年级下册2 圆的对称性教课内容ppt课件，共32页。PPT课件主要包含了对称轴，180度，对称中心，ABBC，知一推二，所在的直线，任意角度，证明连接AC等内容，欢迎下载使用。

【知识再现】1.轴对称图形：平面内，一个图形沿一条直线折叠，_______________________________的图形.这条直线叫做___________. 
　直线两旁的部分能够完全重合　
2.中心对称图形：如果把一个图形绕某一点旋转__________后能与自身重合，这个图形就是中心对称图形.这点叫做_____________. 
【新知预习】1.圆的对称性：(1)圆是轴对称图形，其对称轴是_________________________. (2)圆是中心对称图形，对称中心为_________. 
　任意一条过圆心的直线　
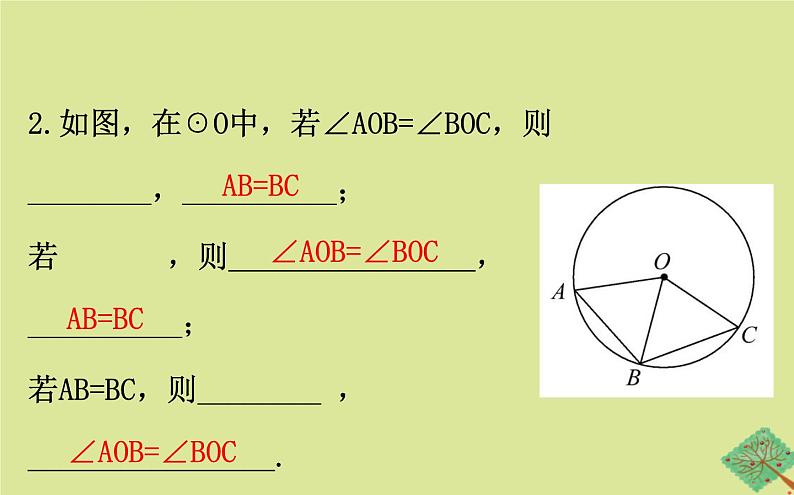
2.如图，在☉O中，若∠AOB=∠BOC，则________，__________； 若 ，则________________，__________； 若AB=BC，则________ ，________________. 
　∠AOB=∠BOC　
归纳：圆心角、弧、弦之间的关系(1)定理：在同圆或等圆中，相等的圆心角所对的弧_________、所对的弦_________. (2)推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量_________，那么它们所对应的其余各组量都分别_________(简称：_____________). 
【基础小练】请自我检测一下预习的效果吧！1.下列结论正确的是(　 　)A.经过圆心的直线是圆的对称轴B.圆的对称轴有1条C.与圆相交的直线是圆的对称轴D.与直径相交的直线是圆的对称轴
2.在☉O与☉O′中，若∠AOB=∠A′O′B′，则AB与A′B′的关系为(　 　)A.AB=A′B′B.AB>A′B′C.AB3.如图，已知AB是☉O的直径，D，C是劣弧EB的三等分点，∠BOC=40°，那么∠AOE=(　 　)A.40°B.60°C.80°D.120°
知识点一 圆的对称性(P72“随堂练习T1”拓展)【典例1】世界上因为有了圆的图案，万物才显得富有生机，如图是来自现实生活中的图形，它们看上去多么美丽和谐，这正是因为它们具有对称性.
(1)请从对称轴的条数方面找出这三个图形中与其他两幅不同的图形.(2)请你再画出两个与上面图案不重复的图案，要体现对称和美观.
【思路点拨】(1)第一幅图形有无数条对称轴.(2)要求：体现对称和美观即可.
【自主解答】(1)第一幅图形有无数条对称轴，所以与其他两幅不同.(2)如图： (答案不唯一，仅供参考)
【题组训练】1.下列图形中对称轴最多的是(　 　)　 A.圆　　B.正方形　　C.等边三角形　　D.线段
★2.将一张圆形的纸片，需至少对折______次，可得到圆心. 
★★3.如图，圆心角∠AOB=20°，将 旋转n°得到 ，则 所对圆心角的度数是_______度.世纪金榜导学号 
【我要做学霸】圆的对称性(1)圆是轴对称图形：它有_________条对称轴，每条直径_______________是其对称轴. (2)圆是中心对称图形：对称中心是圆心，绕圆心旋转_____________都能与原图形重合. 
知识点二 等弧、等弦、圆心角的关系(P71“例”补充)【典例2】如图，在☉O中， ，∠AOB=45°，求∠COD的度数.
【规范解答】 ∴ ，……………………………等式的性质∴∠AOB=∠COD，…………………………等弧、等弦、圆心角的关系∵∠AOB=45°，∴∠COD=45°.……………等量代换
【学霸提醒】“知一推二”及三限定1.“知一推二”在同圆或等圆中，两个圆心角、两条弧、两条弦这三组量中有一组量相等，其余的各组量也分别相等，简称“知一推二”.
2.三限定(1)当已知两个圆心角相等时，必须限定同圆或等圆.(2)当两弦相等推圆心角相等时，必须限定同圆或等圆.(3)当两弦相等推弧相等时，除了限定同圆或等圆之外，还要限定两弧是同一类弧.
【题组训练】1.(2019·道外区期末)如图，AB，CD是☉O的直径， .若∠AOE=32°，则∠COE的度数是(　 　)世纪金榜导学号A.32°B.60°C.68°D.64°
★2.(2019·惠阳区期中)如图，AB是☉O的直径，点C，D在☉O上，∠BOC=100°，AD∥OC，则∠AOD=(　 　)A.20°B.60°C.50°D.40°
★★3.(2019·南京中考)如图，☉O的弦AB，CD的延长线相交于点P，且AB=CD.求证：PA=PC.
【火眼金睛】如图，∠AOB=90°，C，D是 的三等分点，AB分别交OC，OD于点E，F.试找出图中相等的线段(半径除外).
正解：相等的线段：AE=FB，OE=OF.∵C，D为 的三等分点，∴ ∴∠AOC=∠BOD，∵OA=OB，∴∠OAB=∠OBA，∴△AOE≌△BOF，∴AE=FB，OE=OF.
【一题多解】(2019·武汉期末)如图，A，B，C，D是☉O上四点，且AD=CB，∠A=∠C，求证：AB=CD.
【证明】方法一：(利用全等)在△AED和△CEB中，∵AD=CB，∠A=∠C，∠AED=∠CEB，∴△AED≌△CEB，∴AE=EC，DE=BE，∴AE+BE=EC+DE，即AB=CD.
方法二：(利用等弧、等弦、圆心角的关系)