初中北师大版9 弧长及扇形的面积图文ppt课件

这是一份初中北师大版9 弧长及扇形的面积图文ppt课件，共46页。PPT课件主要包含了πr2，解1连接AE，分割为几个规则，规则图形面积等内容，欢迎下载使用。

　【知识再现】1.圆的周长公式：C=　_____　 2.圆的面积公式：S=　____　 
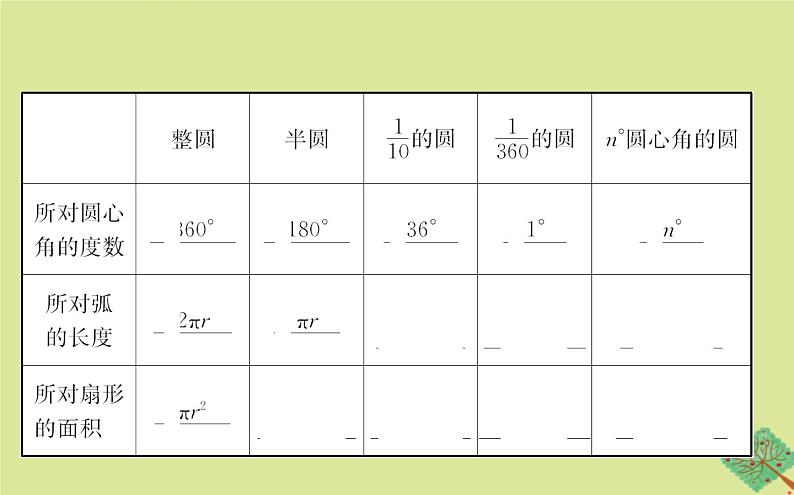
　【新知预习】阅读教材P100-101，解决以下问题：　已知圆的半径为r，根据条件填表：
归纳：1.在半径为R的圆中，n°的圆心角所对的弧长的计算公式为L=　　　　. 2.如果扇形的半径为R，圆心角为n°，那么扇形的面积的计算公式为S=　　　　　. 
3.比较扇形面积公式与弧长公式还可得到S= 　. 
【基础小练】请自我检测一下预习的效果吧！1.已知扇形的半径为12，圆心角为60°，则这个扇形的弧长为(　 　)A.9π　　　　　B.6π C.3π 　　D.4π
2.扇形的面积是12π，它的弧所对的圆心角为30°，则扇形的半径是(　 　)A.8D.10
3.一圆弧的圆心角为150°，它所对的弧长等于半径为5 cm的圆的周长，则该弧所在圆的半径为 (　 　)A.24 cmB.12 cmC.6 cmD.30 cm
4.已知一扇形的弧长是4π，半径为3，那么这个扇形的面积是　____　. 
知识点一 弧长公式及应用(P100例1拓展)【典例1】如图，已知AB是☉O的直径，C，D是☉O上的点，OC∥BD，交AD于点E，连接BC.
(1)求证：AE=ED.(2)若AB=10，∠CBD=36°，求 的长.
【规范解答】(1)∵AB是☉O的直径，∴∠ADB=90°，…………直径所对的圆周角为直角∵OC∥BD，∴∠AEO=∠ADB=90°， …………两直线平行，同位角相等即OC⊥AD，∴AE=ED. …………垂直于弦的直径平分弦
(2)∵OC⊥AD，∴ ， …………垂直于弦的直径平分弦所对的弧∴∠ABC=∠CBD=36°，……等弧所对的圆周角相等∴∠AOC=2∠ABC=2×36°=72°，……圆周角定理∴ 的长= =2π.……弧长公式
【学霸提醒】求与弧长相关计算的两个步骤
【题组训练】1.如图，一段公路的转弯处是一段圆弧( )，则 的展直长度为(　 　)A.3π mB.6π mC.9π mD.12π m
★2.如图，正方形ABCD内接于☉O，AB= ，则 的长是(　 　)A.πB. πC.2πD. π
★3.(2019·青岛中考)如图，线段AB经过☉O的圆心，AC，BD分别与☉O相切于点C，D.若AC=BD=4，∠A=45°，则 的长度为(　 　)A.πB.2πC.2 πD.4π
★★4.(2019·泰安中考)如图，将☉O沿弦AB折叠， 恰好经过圆心O，若☉O的半径为3，则 的长为 (　 　)A. πB.πC.2πD.3π
★★5.(2019·南关区月考)如图，在△ABC中，AB=AC，以AB为直径的☉O分别交AC，BC于点D，E.(1)求证：BE=CE.(2)若AB=6，∠BAC=54°，求 的长.
∵AB是圆O的直径，∴∠AEB=90°，即AE⊥BC.又∵AB=AC，∴AE是边BC上的中线，∴BE=CE.
(2)∵AB=6，∴OA=3.又∵OA=OD，∠BAC=54°，∴∠AOD=180°-2×54°=72°，∴ 的长为：
知识点二 扇形及相关图形阴影面积的计算(P101例2拓展)【典例2】如图，在△ABC中，AB=AC，以边BC为直径的☉O与边AB交于点D，与边AC交于点E，连接OD，OE.
(1)求证：BD=CE.(2)若∠C=55°，BC=10，求图中阴影部分的面积.
【尝试解答】(1)∵AB=AC， ∴　∠B=∠C　，…………等边对等角  …………等量代换∴EC=BD.
(2)∵AB=AC，∴　∠B=∠C=55°　，  …………等边对等角∵OB=OD，OC=OE，∴∠B=∠ODB=55°，∠C=∠OEC=55°， …………等边对等角∴∠BOD=∠EOC=70°，
∴∠DOE=40°，∵BC=10，∴BO=CO=5，∴S阴影=　 =　 .  …………扇形的面积公式计算
【题组训练】1.如图，AB是☉O的直径，CD是弦，∠BCD=30°，OA=2，则阴影部分的面积是(　 　)A. B. C.πD.2π
★2.如图，在▱ABCD中，∠B=60°，☉C的半径为3，则图中阴影部分的面积是(　 　)A. πB.2πC.3πD.6π
★3.(2019·南充中考)如图，在半径为6的☉O中，点A，B，C都在☉O上，四边形OABC是平行四边形，则图中阴影部分的面积为(　 　)A.6πB.3 πC.2 πD.2π
★★4.(2019·盐城滨海一模)如图，在△ABC中，∠ABC=90°，以AB为直径的☉O交AC于点D，点E为BC的中点，连接OD，DE.(1)求证：OD⊥DE.(2)若∠BAC=30°，AB=12，求阴影部分的面积.
解：(1)连接DB.∵AB是☉O的直径，∴∠ADB=90°，∴∠CDB=90°，∵点E是BC的中点，∴DE=CE= BC，∴∠EDC=∠C，
∵OA=OD，∴∠A=∠ADO，∵∠ABC=90°，∴∠A+∠C=90°，∴∠ADO+∠EDC=90°，∴∠ODE=90°，∴OD⊥DE.
(2)∵AB=12，∠BAC=30°，∴AD= ，阴影部分的面积=
【我要做学霸】求不规则阴影面积的“两种方法”1.分割求和法：即将阴影部分___________________的图形，分别求出面积，再相加. 2.补全求差法：即用包含阴影部分的_______________　减去其包含的空白部分面积. 
　【火眼金睛】如图所示，半圆O中，直径AB长为4，C，D为半圆O的三等分点，求阴影部分的面积.
正解：连接OC，OD，∵C，D为半圆O的三等分点，∴∠AOC=∠COD=∠BOD=60°，∵OC=OD，∴△COD为等边三角形，∴∠CDO=∠BOD=60°，
∴CD∥AB，∴S△ACD=S△COD，∴S阴影=S扇形COD= .
　【一题多变】如图，长方形ABCD的周长为28，且AB∶BC=3∶4，求 的长度.
解：由题意知AB=28÷2× =6，∴ 的长度= =3π.
【母题变式】【变式一】(变换条件)如图，长方形ABCD的两边AB∶BC=3∶4， 的长度为8π，求 的长度.
解：∵ 的长= =8π.∴BC=16，∵AB∶BC=3∶4，∴AB=12.∴ 的长度= =6π.
【变式二】(变换问法)如图，长方形ABCD的周长为28，且AB∶BC=3∶4，求图中阴影部分的面积.