初中数学人教版八年级上册15.3 分式方程教学课件ppt

这是一份初中数学人教版八年级上册15.3 分式方程教学课件ppt，文件包含第15章分式章节复习pptx、第15章分式章节复习教学设计docx、第15章分式章节复习导学案docx、第15章分式达标检测解析版docx、第15章分式达标检测原卷版docx等5份课件配套教学资源，其中PPT共60页， 欢迎下载使用。

第15章 分式 章节复习
人教版数学八年级上册
1.理解分式定义，掌握分式有意义的条件；掌握分式的加减乘除运算及混合运算；掌握分式方程的解法，会列分式方程解决实际间题.2.经历“实际问题→分式方程→整式方程”的过程，发展学生分析问题、解决问题的能力，渗透数学的转化思想培养学生的应用意识.3.经历建立分式方程模型解决实际问题的过程，体会数学模型的，应用价值，从而提高学习数学的兴趣.
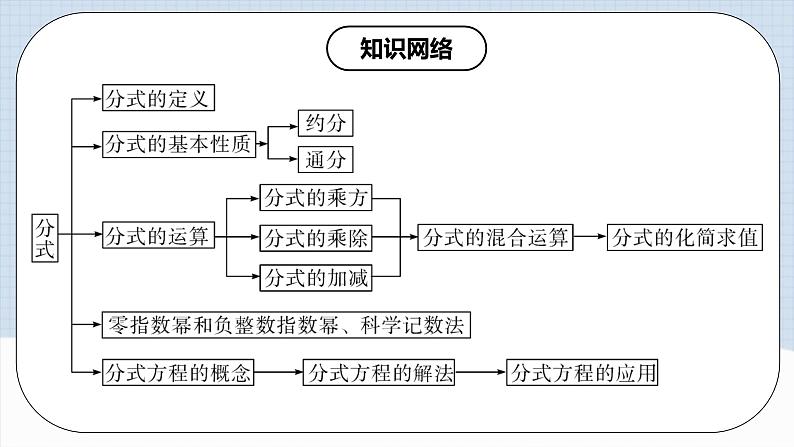
一般地，如果A、B都表示两个整式，并且B中含有字母，那么式子 叫做分式.其中A叫做分式的分子，B为分式的分母.
一、分式
二、分式的基本性质：分式的分子与分母乘(或除以)同一个不等于0的整式，分式的值不变.
根据分式的基本性质，把一个分式的分子与分母的公因式约去，叫做分式的约分.
经过约分后的分式 ， 其分子与分母没有公因式.像这样分子与分母没有公因式的分式，叫做最简分式.
分式的约分，一般要约去分子和分母所有的公因式，使得结果成为最简分式或者整式.
约分的基本步骤
(1)若分子、分母都是单项式，则约去系数的最大公约数，并约去公共字母的最低次幂；(2)若分子、分母含有多项式，则先将多项式分解因式，然后约去分子、分母所有的公因式．
注意事项：（1）约分前后分式的值要相等.（2）约分的关键是确定分式的分子和分母的公因式.（3）约分是对分子、分母的整体进行的，也就是分子的整体和分母的整体都除以同一个因式.
根据分式的基本性质，把几个异分母的分式分别化成与原来的分式相等的同分母的分式，叫做分式的通分.
为通分，要先确定各分式的公分母，一般取各分母的所有因式的最高次幂的积作公分母，它叫做最简公分母.
确定几个分式的最简公分母的一般步骤：（1）分母为多项式的先因式分解；（2）系数：各分式分母系数的最小公倍数；（3）字母：各分母的所有字母的最高次幂；（4）多项式：各分母所有多项式因式的最高次幂；（5）写成积的形式.
【分式的乘除法法则 】 乘法法则：分式乘分式，用分子的积作为积的分子，分母的积作为积的分母. 除法法则：分式除以分式，把除式的分子、分母颠倒位置后，与被除式相乘.
三、分式的乘除
1.分式的分子、分母都是几个因式的积的形式，可先约去分子、分母的公因式，再按照法则进行计算.2.分子或分母是多项式的按以下方法进行：①将原分式中含同一字母的各多项式按降幂(或升幂)排列；在乘除过程中遇到整式则视其为分母为1，分子为这个整式的分式；②把各分式中分子或分母里的多项式分解因式；③应用分式乘除法法则进行运算；(注意:结果为最简分式或整式．)
分式乘除法的解题步骤
四、分式的乘方
【同分母分式加减法的法则】 同分母分式相加减，分母不变，把分子相加减.
【异分母分式加减法的法则】 异分母分式相加减，先通分，变为同分母的分式，再加减.
异分母分式通分时，通常取最简公分母作为它们的共同分母.
五、分式的加减
分式的混合运算（1）进行混合运算时，要注意运算顺序，在没有括号的情况下，按从左往右的方向，先算乘方，再算乘除，后算加减；（2）分式的混合运算，一般按常规运算顺序，但有时应先根据题目的特点，运用运算律进行灵活运算.
混合运算的特点：是整式运算、因式分解、分式运算的综合运用，综合性强.
分式的混合运算顺序：先算乘方，再算乘除，最后算加减，有括号的先算括号里面的.计算结果要化为最简分式或整式．
六、分式的混合运算
一般地，我们规定：当n是正整数时，
这就是说，a-n (a≠0)是an的倒数.
七、整数指数幂
类似地，我们可以利用10的负整数次幂，用科学记数法表示一些绝对值较小的数，即将它们表示成a×10-n的形式，其中n是正整数，1≤∣a∣＜10.
用科学记数法表示绝对值小于1的数的两种方法：方法1：n 等于原数中左起第一个非0数前0的个数(包括小数点前的那个0)；方法2：小数点向右移到第一个非0的数后，小数点移动了几位，n就等于几.
八、用科学记数法表示绝对值小于1的数
分母中含有未知数的方程叫做分式方程.
注：(1)分式方程的主要特征：含分母且分母里含有未知数. (2)分式方程和整式方程的区别就在于分母中是否含有未知数.
1.在方程的两边都乘以最简公分母，约去分母，化成整式方程.2.解这个整式方程.3.把整式方程的解代入最简公分母，如果最简公分母的值不为0，则整式方程的解是原分式方程的解，否则原分式方程无解；4.写出原方程的根.
简记为：“一化二解三检验”.
“去分母法”解分式方程的步骤：
九、分式方程及其解法
解分式方程的一般步骤如下：
分式方程
整式方程
去分母
x=a
解整式方程
检验
最简公分母为0
x=a不是分式方程的解
最简公分母不为0
x=a是分式方程的解
十、分式方程的应用
列分式方程解应用题的一般步骤
1.审:清题意，并设未知数； 2.找:相等关系；3.列:出方程；4.解:这个分式方程；5.验:根（包括两方面 :(1)是否是分式方程的根；(2)是否符合题意）；6.写:答案.
例1.下列各式哪些是整式？哪些是分式？
整式
整式
分式
整式
分式
整式
分式
整式
整式
分式
例2.已知分式 有意义，则x应满足的条件是 (　　) A.x≠1 B．x≠2 C.x≠1且x≠2 D.以上结果都不对
C
【点睛】分式有意义的条件是分母不为零.如果分母是几个因式乘积的形式，则每个因式都不为零.
解：当分子等于零而分母不等于零时,分式的值为零.则x2-1=0，∴x=±1，而x+1≠0，∴x≠-1.∴当x=1时分式 的值为零.
例3.当x为何值时，分式 的值为零?
 
 
D
 
C
D
【1-3】若 的值为零，则x＝ ．
－3
　例5.填空：
(1) (2)
(3) (4)
 
 
B
 
例8.约分：(1) (2) (3)
分析：为约分，要先找出分子和分母的公因式.
解：(1)
找公因式方法：
（1）分子、分母系数的最大公约数；（2）分子、分母公共字母的最低次幂.
(公因式是5abc)
例8.约分：(1) (2) (3)
解：(2)
分析：约分时,分子或分母若是多项式，能分解则先进行因式分解，再找出分子和分母的公因式进行约分.
(3)
 
 
【2-1】不改变分式的值，把下列各式的分子与分母的各项系数都化为整数.
 
 
 
 
 
 
 
 
 
 
 
 
C
D
 
 
②
例11.计算：(1) (2)
解：
(1)
(2)
【点睛】进行分式的乘除、乘方混合运算时，要严格按照运算顺序进行运算．先算乘方，再算乘除．注意结果一定要化成一个整式或最简分式的形式．
例12.计算：(1) (2)
 
 
 
 
 
A
B
【4-3】在下列各式中:① ; ② ;③ ; ④ .相等的两个式子是( )A.①② B.①③ C.②③ D.③④【4-4】如果 ，那么a8b4等于( )A.6 B.9 C.12 D.81
C
B
例13.计算：
 
 
 
例13.计算：
 
 
 
 
例15.甲工程队完成一项工程需n天，乙工程队要比甲队多用3天才能完成这项工程，两队共同工作一天完成这项工程的几分之几？
解：甲工程队一天完成这项工程的 ，乙工程队一天完成这项工程的 ，两队共同工作一天完成这项工程的
 
1
 
【5-3】计算：
 
 
 
 
 
 
例16.计算：(1) (2)
解：原式
 
C
【6-2】下面是涂涂同学完成的一组分式化简的练习题，每小题20分，他能得的分数是（　 ）A．40分 B．60分 C．80分 D．100分
A
 
 
 
 
 
 
根据分式有意义的条件得：x≠1，x≠2，∴取x=0，原式=2.
【点睛】把分式化成最简分式是解题的关键，通分、因式分解和约分是基本环节，注意选数时，要求分母不能为0.
 
D
 
 
 
 
 
 
例18.计算：
 
(1)a-2b2·(a2b-2)-3
(2)(2ab2c-3)-2÷(a-2b)3
【点睛】对于这类运算先进行幂的乘方，再进行幂的乘除，最后将整数指数幂化成正整数指数幂．
例19.计算：
分析：分别根据有理数的乘方、0指数幂、负整数指数幂及绝对值的性质计算出各数，再根据实数的运算法则进行计算．
解：
 
C
D
B
 
 
 
 
【8-5】计算：
解：
例20.把下列各数用科学记数法表示出来：（1）650000；（2）-36900000；（3）0.0000021；（4）-0.00000657.
 
例21.用小数表示下列各数：(1)2×10－7； (2)3.14×10－5； (3)7.08×10－3； (4)2.17×10－1.
解析：小数点向左移动相应的位数即可．
解：(1)2×10－7＝0.0000002；(2)3.14×10－5＝0.0000314；(3)7.08×10－3＝0.00708；(4)2.17×10－1＝0.217.
 
 
（2）原式=4×10-6×3×10-3=（4×3）×（10-6×10-3）=12×10-9=1.2×10-8；
（3）原式=-0.5×10-3=-5×10-4.
【9-1】下列用科学记数法表示的算式:①236400000=2.364×105;②-1020000000=-1.02×109;③0.0000001001=1.001×10-7;④-0.000083=-8.3×10-6.其中不正确的有( )A.0个 B.1个 C. 2个 D.3个
C
【9-2】比较大小: (横线上填“>”“<”或“=”)(1)7.253×10-8_____7.253×10-7(2)5.3×10-5_____0.0000053(3)3.56×10-6_____2.25×10-6(4)-2.6×10-9_____-3.25×10-10(5)8.53×109_____1.01×1010
<
>
>
<
<
 
 
例23.下列方程中，哪些是分式方程？哪些是整式方程？
【点睛】判断一个方程是否为分式方程，主要是看分母中是否含有未知数(注意：π不是未知数)．
分式方程
整式方程
分式方程
分式方程
分式方程
分式方程
整式方程
整式方程
例24.解方程:
解：方程两边乘(x-1)(x+2)，得 x(x+2)-(x-1)(x+2)=3 解得 x=1检验：当x=1时，(x-1)(x+2)=0，因此x=1不是原分式方程的解.所以，原分式方程无解.
 
A
D
 
C
解：(1)方程两边乘(x+1)(x-1)，得 2(x+1)=4 解得 x=1检验：当x=1时，(x+1)(x-1)=0，因此x=1不是原分式方程的解.所以，原分式方程无解.
解:(2)方程两边乘(x-2),得1=-(1-x)-3(x-2)解得x=2检验:当x=2时, x-2=0，因此x=2不是原分式方程的解.所以，原分式方程无解.
【10-4】解方程：
 
 
A
【点睛】求出方程的解(用未知字母表示)，然后根据解的正负性，列关于未知字母的不等式求解，特别注意分母不能为0.
 
 
 
 
 
 
 
 
 
a≤6且a≠3
 
 
 
 
例28.在社会主义新农村建设中，某乡镇决定对一段公路进行改造．已知这项改造工程由甲工程队单独做需要40天完成；如果由乙工程队先单独做10天，那么剩下的工程还需要两队合做20天才能完成．(1)求乙工程队单独完成这项工程所需的天数；(2)若两队合做这项工程，求完成工程所需的天数．(3)若甲队的费用每天1200元，乙队每天850元，可以有哪些施工方案？怎样施工费用最低？
 
 
 
 
 
 
A
 
B
【12-3】科技创新加速中国高铁技术发展，某建筑集团承担一座高架桥的铺设任务，在合同期内高效完成了任务，这是记者与该集团工程师的一段对话：记者：你们是用10天完成4500米长的高架桥铺设任务的？工程师：是的，我们铺设500米后，采用新的铺设技术，这样每天铺设长度是原来的2倍．(1)通过这段对话，请你求出该建筑集团原来每天铺设高架桥的长度．(2)请求出该建筑集团是提前多少天完成铺设任务的？