初中数学人教版九年级上册21.1 一元二次方程教案
展开实际问题与一元二次方程
一、教材分析
本节是在学习学习了一元二次方程解法后,解决生活中的实际问题,重点是分析实际问题中的数量关系并以方程形式进行表示的这种数学建模思想。
二、学情分析
学生已经学会了一元二次方程的解法,并且能在实际问题中抽象和建立一元一次方程、可化为一次方程的分式方程的模型,从而在此基础上建立一元二次模型则水到渠成.
三、教学目标
1.知识与能力
(1)、掌握面积法建立一元二次方程的数学模型并运用它解决实际问题.
(2)、 能根据具体问题的实际意义,检验结果是否合理.
2.过程与方法
在解决实际问题的过程中体会知识间的关系,感受数学与生活的联系.
3.情感、态度与价值观
培养学生分析解决问题的能力,体会数学知识应用的价值.
四、重点、难点
重点:据面积与面积之间的等量关系建立一元二元方程的数学模型并运用它解决实际问题.
难点:根据面积与面积之间的等量关系建立一元二次方程的数学模型
五、教学设计
教学环节 | 教学活动设计 | 设计意图说明 |
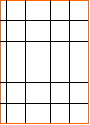
导学求思 | 一副风景画长27㎝,宽21㎝,正中央是一个矩形,如果要使图片面积是整个面积的四分之三,上、下、左、右边衬等宽,应如何设计四周边衬的宽度?(只解设、列方程)
| 以学校一教师的画展导入课题,贴近学生的生活,激发兴趣。 四周边衬等宽易于解决,为探究埋下伏笔。 |
探究交流 | (探究3)如上图,要设计另一幅画长27cm,宽21cm,正中央是一个与整个画面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是整个面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位)? 自学指导:1、题目等量关系是什么? 2、如何设未知数?3、你还有其他方法列方程吗?
| 自学指导2是本活动中学环节,通过学生充分讨论,得出多种不同方法,激发学生学习热情,使学生体会解决问题方法的多样性。 |
试一试 |
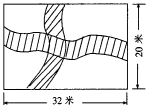
思考:以上2图有什么联系和区别? 还有下面几种方案:在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种上草坪,要使草坪的面积为540m2,求道路的宽。(只写解设、列出方程即可)
| 试一试中,思考中的问题是中心环节,以图形对比的问题为引导,通过对比两个图形的联系和区别,启发学生以边框问题为模型,构建草坪问题的解题思路。
充分思考之后,学生会产生动手实践的欲望,教师要给学生一定的空间,同时也注意对图形变换的指导。 |
测一测 |
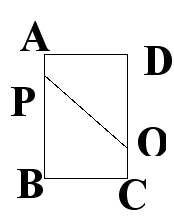
2、选做,如图,已知A、B、C、D为矩形的四个顶点,AB=16㎝,AD=6㎝,动点P、Q分别从点A、C同时出发,点P以3㎝/s的速度向点B移动,一直到点B为止,点Q以2㎝/s的速度向点D移动. 问:P、Q两点从出发开始几秒时,四边形PBCQ的面积是33c㎡
| 巩固所学知识,通过检测了解学生的掌握情况,并通过选做题开阔学生视野。. |
评价反思 | 谈谈本节课的收获:
| 引导学生逐步学会总结,对知识脉络有更清晰的认识。. |
作业 | 48页8、53页8、11 | 巩固练习 |
初中数学人教版八年级上册15.1.2 分式的基本性质教案及反思: 这是一份初中数学人教版八年级上册15.1.2 分式的基本性质教案及反思,共2页。教案主要包含了 情景引入,学习新课,问题拓展,课堂小结,作业布置等内容,欢迎下载使用。
人教版七年级下册第八章 二元一次方程组8.3 实际问题与二元一次方程组教学设计: 这是一份人教版七年级下册第八章 二元一次方程组8.3 实际问题与二元一次方程组教学设计,共2页。教案主要包含了知识与技能,过程与方法,应用等内容,欢迎下载使用。
初中5.2 统计的简单应用精品教案设计: 这是一份初中5.2 统计的简单应用精品教案设计,共6页。