初中数学人教版九年级上册21.1 一元二次方程教案

这是一份初中数学人教版九年级上册21.1 一元二次方程教案，共4页。
 直线和圆的位置关系教学目标(一)教学知识点1．理解直线与圆有相交、相切、相离三种位置关系．2．了解切线的概念，探索切线与过切点的直径之间的关系．3．能判定一条直线是否为圆的切线(二)能力训练要求1．经历探索直线与圆位置关系的过程，培养学生的探索能力．2．通过观察得出“圆心到直线的距离d和半径r的数量关系”与“直线和圆的位置关系”的对应与等价，从而实现位置关系与数量关系的相互转化．(三)情感与价值观要求通过探索直线与圆的位置关系的过程，体验数学活动充满着探索与创造，感受数学的严谨性以及数学结论的确定性．在数学学习活动中获得成功的体验，锻炼克服困难的意志，建立自信心．教学重点经历探索直线与圆位置关系的过程．理解直线与圆的三种位置关系．了解切线的概念以及切线的性质．教学难点经历探索直线与圆的位置关系的过程，归纳总结出直线与圆的三种位置关系．探索圆的切线的性质．教学方法教师指导学生探索法．教学过程Ⅰ．创设问题情境，引入新课[师]我们在前面学过点和圆的位置关系，请大家回忆它们的位置关系有哪些？[生]圆是平面上到定点的距离等于定长的所有点组成的图形．即圆上的点到圆心的距离等于半径；圆的内部到圆心的距离小于半径；圆的外部到圆心的距离大于半径．因此点和圆的位置关系有三种，即点在圆上、点在圆内和点在圆外．也可以把点与圆心的距离和半径作比较，若距离大于半径在圆外，等于半径在圆上，小于半径在圆内．[师]本节课我们将类比地学习直线和圆的位置关系．Ⅱ．新课讲解１．探索直线与圆的三种位置关系[师]直线和圆的位置关系，我们在现实生活中随处可见，只要大家注意观察，这样的例子是很多的．观察幻灯片中的三幅照片，地平线和太阳的位置关系怎样？作一个圆，把直尺的边缘看成一条直线，固定圆，平移直尺，直线和圆有几种位置关系？[生]把太阳看作圆，地平线看作直线，则直线和圆有三种位置关系；把直尺的边缘看成一条直线，则直线和圆有三种位置关系．[师]从上面的举例中，大家能否得出结论，直线和圆的位置关系有几种呢？[生]有三种位置关系：[师]直线和圆有三种位置关系，如下图：它们分别是相交、相切、相离．当直线与圆相切时(即直线和圆有唯一公共点)，这条直线叫做圆的切线当直线与圆有两个公共点时，叫做直线和圆相交．当直线与圆没有公共点时，叫做直线和圆相离．因此，从直线与圆有公共点的个数可以断定是哪一种位置关系，你能总结吗？[生]当直线与圆有唯一公共点时，这时直线与圆相切；当直线与圆有两个公共点时，这时直线与圆相交；当直线与圆没有公共点时，这时直线与圆相离．[师]能否根据点和圆的位置关系，点到圆心的距离d和半径r作比较，类似地推导出如何用点到直线的距离d和半径r之间的关系来确定三种位置关系呢？[生]如上图中，圆心O到直线l的距离为d，圆的半径为r，当直线与圆相交时，d＜r；当直线与圆相切时，d＝r；当直线与圆相离时，d＞r，因此可以用d与r间的大小关系断定直线与圆的位置关系．[师]由此可知：判断直线与圆的位置关系有两种方法．一种是从直线与圆的公共点的个数来断定；一种是用d与r的大小关系来断定．(1)从公共点的个数来判断：直线与圆有两个公共点时，直线与圆相交；直线与圆有唯一公共点时，直线与圆相切；直线与圆没有公共点时，直线与圆相离．(2)从点到直线的距离d与半径r的大小关系来判断：d＜r时，直线与圆相交；d＝r时，直线与圆相切；d＞r时，直线与圆相离． [例1]已知Rt△ABC的斜边AB＝8cm，AC＝4cm．(1)以点C为圆心作圆，当半径为多长时，AB与⊙C相切？(2)以点C为圆心，分别以2cm和4cm的长为半径作两个圆，这两个圆与AB分别有怎样的位置关系？ 分析：根据d与r间的数量关系可知：d＝r时，相切；d＜r时，相交；d＞r时，相离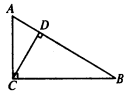．解：(1)如上图，过点C作AB的垂线段CD．∵AC＝4cm，AB＝8cm；∴cosA＝，∴∠A＝60°．∴CD＝ACsinA＝4sin60°＝2(cm)．因此，当半径长为2cm时，AB与⊙C相切．(2)由(1)可知，圆心C到AB的距离d＝2cm，所以，当r＝2cm时，d＞r，⊙C与AB相离；当r＝4cm时，d＜r，⊙C与AB相交．２．探究切线的判断方法思考：在⊙O中,经过半径OA的外端点A作直线l⊥OA,则圆心O到直线l的距离是多少?直线L和⊙O有什么位置关系? 教师得出结论：经过半径的外端并且垂直于这条半径的直线是圆的切线.强调：切线必须同时满足两条：①经过半径外端；②垂直于这条半径． 几何语言：∵OA⊥l ,OA是⊙O的半径 ∴l是⊙O的切线３．教师总结：证明直线与圆相切的三种途径：⑴定义法:和圆有且只有一个公共点的直线是圆的切线.⑵数量法(d=r):和圆心距离等于半径的直线是圆的切线.⑶判定定理:经过半径外端且垂直于这条半径的直线是 圆的切线.即:若直线与圆的一个公共点已指明,则连接这点和圆心,说明直线垂直于经过这点的半径;若直线与圆的公共点未指明,则过圆心作直线的垂线段,然后说明这条线段的长等于圆的半径．４．例题讲解幻灯片出示例２、例３教师讲解，板书过程Ⅲ．巩固练习1.判断下列命题是否正确．      (1)经过半径外端的直线是圆的切线．(           )    (2)垂直于半径的直线是圆的切线．(         )    (3)过直径的外端并且垂直于这条直径的直线是圆的切线．(       )    (4)和圆只有一个公共点的直线是圆的切线．(    )    (5)以等腰三角形的顶点为圆心，底边上的高为半径的圆与底边相切．(            )(6)直线与圆最多有两个公共点                    （ 　 ）  　(7)若直线与圆相交，则直线上的点都在圆内    (       )   　(8)若A、B是⊙O外两点， 则直线AB与⊙O相离(       )(9)若C为⊙O内与O点不重合的一点，则直线CO与⊙O相交                                               (10)若线段和圆没有公共点,该圆圆心到线段的距离大于半径                                                               2.已知圆的直径为13cm，设直线和圆心的距离为d ：1)若d=4.5cm ,则直线与圆　　　, 直线与圆有____个公共点.         2)若d=6.5cm ,则直线与圆______, 直线与圆有____个公共点3)若d= 8 cm ,则直线与圆______, 直线与圆有____个公共点. 3.已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据    条件填写d的范围:1)若AB和⊙O相离, 则                           ; 2)若AB和⊙O相切, 则                           3)若AB和⊙O相交,则                              .Ⅳ．课时小结本节课学习了如下内容：1．直线与圆的三种位置关系．(1)从公共点数来判断．(2)从d与r间的数量关系来判断．2．圆的切线的性质：圆的切线垂直于过切点的半径．3．例题讲解．Ⅴ．课后作业•        课本98页   练习1.2•        课本101页   习题1.2