人教版九年级上册21.1 一元二次方程导学案及答案

　实际问题与二次函数

-----图形面积最大问题(导学案)

学习目标：

1.能够表示实际问题中变量之间的二次函数关系，会运用二次函数的知识求出实际问题的最值。

2.体会数学与生活是密不可分的，进一步感受数学的应用价值。

教学重点：利用二次函数y=（a≠0）的图象与性质，求面积最值问题

教学难点：1、正确构建数学模型

          2、对函数图象顶点、端点与最值关系的理解与应用

一．自主复习

1.二次函数y=ax2+bx+c的图象是一条             ，它的对称轴是                   ，

顶点坐标是                      .

当a>0时，抛物线开口向        ，有最      点，函数有最      值，是                 。

当 a<0时，抛物线开口向       ，有最       点，函数有最       值，是           。

2.抛物线y＝2x2＋4x-3的顶点坐标是             ,当 x=         时，函数有最         值是y=            .

3.抛物线y=- x2+4x+5 的顶点坐标是           ,当x=        时，函数有最     值是y=           

二．探究实际问题

例：给你总长为 60 m 的篱笆围成矩形花园，请你让花园的的面积 S 最大？并求出最大面积是多少？

三．归纳探究，总结方法

四．小试牛刀

问题：已知直角三角形两条直角边的和等于8，两条直角边各为多长时，这个直角三角形的面积最大？最大面积是多少？

•            应用新知，拓展训练

   如图，有一堵12米的墙，一面靠墙的空地上用长为48米的篱笆，围成中间有二道篱笆的长方形花圃 ，求围成花圃的最大面积（篱笆面积忽略不计）。

•            课堂小结

•         本堂课我学到了什么？

•         这节课应该注意什么？

课外思考题：

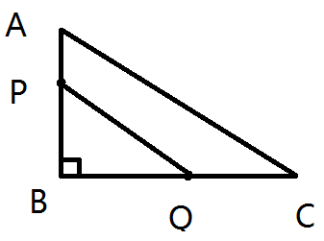
    如图，中 ，∠B=90°，AB=6cm，BC=12cm，点P从A开始沿AB边向B以1cm/s的速度移动；点Q从B开始沿BC边向C以2cm/s的速度移动。如果P、Q同时出发，问经过几秒钟,△PQB的面积最大？最大面积是多少？