新高一预习：题型分类细讲精练09 奇偶性应用归类（人教数学A版2019必修第一册）

这是一份新高一预习：题型分类细讲精练09 奇偶性应用归类（人教数学A版2019必修第一册），文件包含专题09奇偶性应用归类人教A版2019必修第一册解析版docx、专题09奇偶性应用归类人教A版2019必修第一册原卷版docx等2份试卷配套教学资源，其中试卷共52页， 欢迎下载使用。
目录
TOC \ "1-1" \h \u \l "_Tc28969" 【题型一】奇偶性概念辨析 PAGEREF _Tc28969 2
\l "_Tc15310" 【题型二】常见函数奇偶性判断 PAGEREF _Tc15310 3
\l "_Tc13234" 【题型三】奇偶函数与图像 PAGEREF _Tc13234 3
\l "_Tc5889" 【题型四】抽象函数奇偶性判断 PAGEREF _Tc5889 5
\l "_Tc21716" 【题型五】“平移”函数奇偶性 PAGEREF _Tc21716 5
\l "_Tc18952" 【题型六】利用奇偶性求解析式 PAGEREF _Tc18952 6
\l "_Tc27795" 【题型七】奇偶函数混合型求解析式 PAGEREF _Tc27795 6
\l "_Tc5101" 【题型八】利用奇偶性求函数值 PAGEREF _Tc5101 7
\l "_Tc28826" 【题型九】利用奇偶性求和 PAGEREF _Tc28826 7
\l "_Tc9041" 【题型十】利用奇偶性解方程、不等式 PAGEREF _Tc9041 8
\l "_Tc11813" 【题型十一】不等式恒成立求参 PAGEREF _Tc11813 8
\l "_Tc27953" 【题型十二】利用奇偶性求抽象函数恒成立参数 PAGEREF _Tc27953 8
\l "_Tc30751" 【题型十三】利用奇偶性求最值与范围 PAGEREF _Tc30751 9
\l "_Tc2830" 【题型十四】利用奇偶性质推导周期 PAGEREF _Tc2830 9
\l "_Tc21318" 培优第一阶——基础过关练 PAGEREF _Tc21318 10
\l "_Tc25347" 培优第二阶——能力提升练 PAGEREF _Tc25347 12
\l "_Tc30801" 培优第三阶——培优拔尖练 PAGEREF _Tc30801 13
综述：
奇偶性
(1)奇偶函数的性质
①偶函数⇔f(－x)＝f(x) ⇔关于y轴对称⇔对称区间的单调性相反；
②奇函数⇔f(－x)＝－f(x) ⇔关于原点对称⇔对称区间的单调性相同；
③奇函数在x＝0处有意义时，必有结论 f(0)＝0 ；
(2)奇偶性的判定
①“奇±奇”是奇 ，“偶±偶”是 偶 ，“奇×/÷奇”是 偶 ，“偶×/÷偶”是 偶 ，“奇×/÷偶”是 奇 ；
②奇(偶)函数倒数或相反数运算，奇偶性不变；
③奇(偶)函数的绝对值运算，函数的奇偶性均为偶函数．
(2)常见奇函数
①f(x)＝eq \f(ax－1,ax＋1)
②f(x)＝lgaeq \f(x－b,x＋b)
③f(x)＝g(x)－g(－x)
④f(x)＝lga(eq \r(,x2＋1)＋x)
当然，还有f(x)＝sin x，f(x)＝tan x等等；
奇偶性（对称型）与周期
周期性：①若f(x＋a)＝f(x－b) ⇔f(x)周期为T＝a＋b.
②常见的周期函数有：
f(x＋a)＝－f(x)或f(x＋a)＝eq \f(1,f（x）)或f(x＋a)＝－eq \f(1,f（x）)，那么函数f(x)是周期函数，其中一个周期均为T＝2a.
【题型一】奇偶性概念辨析
【典例分析】
函数为奇函数，为偶函数，在公共定义域内，下列结论一定正确的是（ ）
A．为奇函数B．为偶函数
C．为奇函数D．为偶函数
【变式训练】
1.函数，，（ ）
A．是奇函数不是偶函数B．是偶函数不是奇函数
C．既是奇函数又是偶函数D．既不是奇函数也不是偶函数
2.下面四个结论中，正确的个数是（ ）
①奇函数的图象关于原点对称； ②奇函数的图象一定通过原点；
③偶函数的图象关于轴对称； ④偶函数的图象一定与轴相交．
A．1B．2C．3D．4
3.对于函数，“的图象关于轴对称”是“是偶函数”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【题型二】常见函数奇偶性判断
【典例分析】
．符号表示不超过x的最大整数，如，，，定义函数，以下结论正确的是（ ）
①函数的定义域是R，值域为[0,1)；
②方程有无数个解；
③函数是奇函数；
④函数是增函数.
A．①②B．②③C．①②③D．②③④
【变式训练】
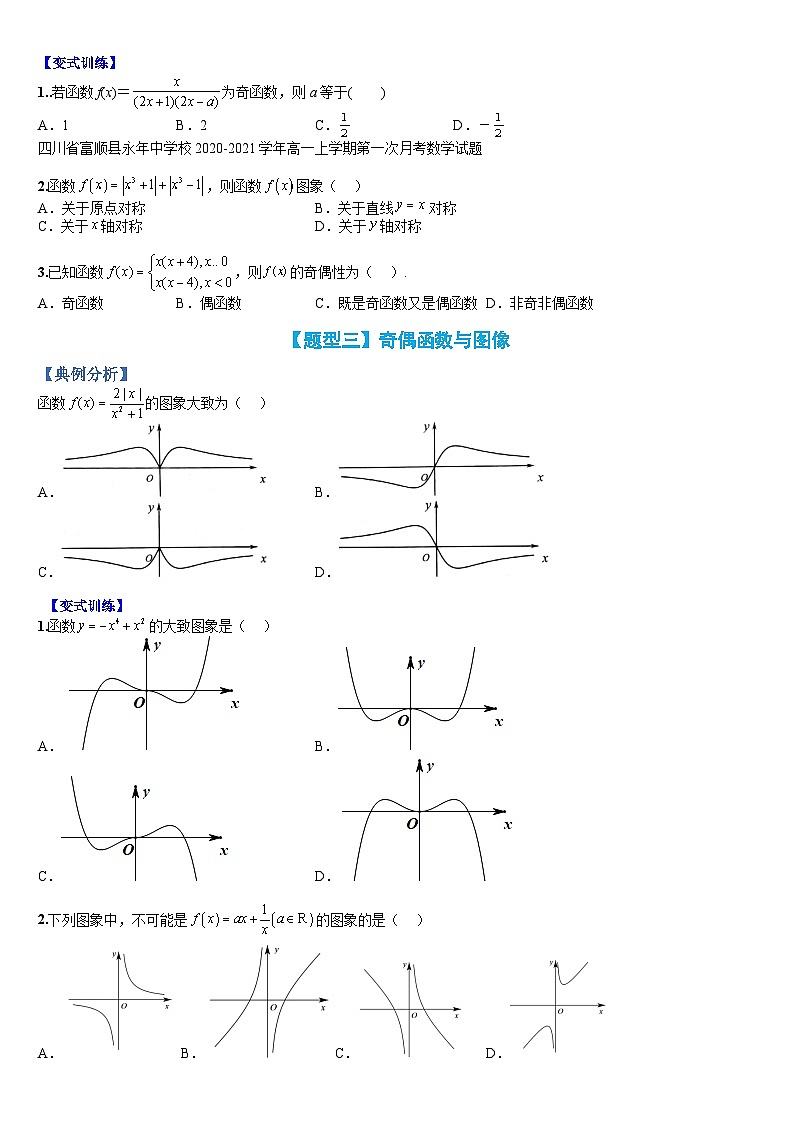
1..若函数f(x)＝为奇函数，则a等于( )
A．1B．2C．D．－
四川省富顺县永年中学校2020-2021学年高一上学期第一次月考数学试题
2.函数，则函数图象（ ）
A．关于原点对称B．关于直线对称
C．关于轴对称D．关于轴对称
3.已知函数，则的奇偶性为（ ）.
A．奇函数B．偶函数C．既是奇函数又是偶函数D．非奇非偶函数

【题型三】奇偶函数与图像
【典例分析】
函数的图象大致为（ ）
A．B．
C．D．
【变式训练】
1.函数的大致图象是（ ）
A．B．
C．D．
2.下列图象中，不可能是的图象的是（ ）
A．B．C．D．
3.函数与的图像如下图，则函数的图像可能是（ ）
A．B．C．D．
【题型四】抽象函数奇偶性判断
【典例分析】
已知对于任意、，都有，，则（ ）
A．是奇函数但不是偶函数B．既是奇函数又是偶函数
C．既不是奇函数也不是偶函数D．是偶函数但不是奇函数
【变式训练】
1.设函数的定义域为，对任意实数，，只要，就有成立，则函数（ ）
A．一定是奇函数B．一定是偶函数C．既是奇函数又是偶函数D．既不是奇函数也不是偶函数
2.若函数对于任意实数满足，则下列关于函数奇偶性说法一定正确的是（ ）
A．是偶函数但不是奇函数B．是奇函数但不是偶函数
C．是非奇非偶函数D．可能是奇函数也可能是偶函数
3.若定义在上的函数满足：对于任意的、，恒有，则函数为（ ）
A．奇函数B．偶函数C．非奇非偶函数D．无法判断奇偶性
【题型五】“平移”函数奇偶性
【典例分析】
已知函数满足，下列四个选项一定正确的是（ ）
A．是偶函数B．是奇函数
C．是奇函数D．是偶函数
【变式训练】
1.用列表法将函数表示为（见表格）则下列判断正确的是（ ）
A．为奇函数B．为偶函数C．为奇函数D．为偶函数
2.若函数，则以下函数为奇函数的是（ ）
A．B．C．D．
3.设函数，则下列函数中为偶函数的是（ ）
A．B．
C．D．
【题型六】利用奇偶性求解析式
【典例分析】
若函数是定义在上的奇函数，且满足，当时，，则当时，函数的解析式为（ ）
A．B．C．D．
【变式训练】
1.设是定义在上的偶函数，且满足，当时，，则时，___________________.
2.已知函数是定义在R上的奇函数，且满足，当时，，则当时，（ ）
A．B．
C．D．
3..若函数在上是奇函数，则的解析式为．
A．B．
C．D．
【题型七】奇偶函数混合型求解析式
【典例分析】
函数和分别是定义在上的奇函数和偶函数，且，则函数的单调增区间为（ ）
A．B．C．D．
【变式训练】
1.已知函数与分别是定义域上的奇函数与偶函数，且，则
A．B．C．-3D．
2.已知是上的奇函数，是上的偶函数，且，则（ ）
A．5B．6C．8D．10
3.定义在上的偶函数和奇函数满足，若恒成立，则实数的取值范围为（ ）
A．B．C．D．
【题型八】利用奇偶性求函数值
【典例分析】
已知函数的定义域为R，且对任意恒成立，又函数的图象关于点对称，且，则（ ）
A．2021B．C．2022D．
【变式训练】
1.已知函数为奇函数，且，则（ ）
A．B．7C．0D．2
2.已知是定义在上的奇函数，，且，则（ ）
A．1B．0C．D．
3..已知是定义在上的偶函数，对任意都有，则________.
【题型九】利用奇偶性求和
【典例分析】
已知定义在上的函数，对任意，都有且，则的值为_________
【变式训练】
1.已知函数是定义域为的奇函数满足.若，则___________.
2.已知是R上的偶函数，若的图象向右平移一个单位后，则得到一个奇函数的图象，则的值为 （ ）
A．1 B．0 C．-1 D．
3.已知是定义域为的奇函数，满足.若，则（ ）
A．-2019B．1C．0D．2019
【题型十】利用奇偶性解方程、不等式
【典例分析】
已知函数是定义在上的奇函数，且当时，，则方程的所有解的和为（ ）
A．B．1C．3D．5
【变式训练】
1.已知是定义在上的奇函数，当时，，则不等式的解集为（ ）
A．B．
C．D．
2.已知是定义在上的奇函数，且当时，．若，则的解集是（ ）
A．B．
C．D．
3.已知定义域为的奇函数，当时，，则不等式的解集为__________．
【题型十一】不等式恒成立求参
【典例分析】
已知定义在上的奇函数满足：时，，且关于的不等式在区间上恒成立，则实数的取值范围为______．
【变式训练】
1.设是定义在R上的奇函数，且当时，，若对于任意的，不等式恒成立，则实数t的取值范围是______．
2.设函数是定义在上的奇函数，当时，，其中，若对任意的，都有，则实数的取值范围为___．
3.已知奇函数的定义域为，且在上单调递增，若实数满足，则的取值范围为（ ）
A．B．C．D．
【题型十二】利用奇偶性求抽象函数恒成立参数
【典例分析】
已知f（x）是定义在[﹣1，1]上的奇函数，且f（﹣1）＝﹣1，当a，b∈[﹣1，1]，且a+b≠0时，（a+b）（f（a）+f（b））＞0成立，若f（x）＜m2﹣2tm+1对任意的t∈[﹣1，1]恒成立，则实数m的取值范围是（ ）
A．（﹣∞，﹣2）∪{0}∪（2，+∞）B．（﹣∞，﹣2）∪（2，+∞）
C．（﹣2，2）D．（﹣2，0）∪（0，2）
【变式训练】
1.已知定义在上的函数满足，且在上单调递减，若对任意的，恒成立，则实数的取值范围为（ ）
A．B．C．D．
2..已知定义在上的函数在上单调递减，且是偶函数，不等式对任意的恒成立，则实数的取值范围是
A．B．C．D．
3.已知函数的定义域，且对任意，恒有，当时，，若，则m的取值范围为__________.
【题型十三】利用奇偶性求最值与范围
【典例分析】
若对任意，有，则函数在上的最大值与最小值的和（ ）
A．B．6C．D．5
【变式训练】
1.已知是偶函数，当时，，若当时，恒成立，则的最小值为( )
A．B．C．D．1
2.已知函数是定义在上的奇函数，且满足，当时，，则当时，的最小值为（ ）
A．B．C．D．
3..函数是定义域为的奇函数，且，已知，，则函数的最小值为（ ）
A．-2B．-1C．D．0
【题型十四】利用奇偶性质推导周期
【典例分析】
设函数定义域为R，为奇函数，为偶函数，当时，，则下列结论错误的是（ ）
A．B．为奇函数
C．在上为减函数D．的一个周期为8
【变式训练】
1.函数的定义域为，若是奇函数，是偶函数，则（ ）
A．是偶函数B．
C．D．
2.设函数的定义域为R，为奇函数，为偶函数，当时，．若，则（ ）
A．B．C．D．
3.设函数的定义域为，为奇函数，为偶函数，当时，．若，则（ ）
A．B．C．D．
分阶培优练
培优第一阶——基础过关练
1.下列说法正确的是（ ）
A．若一个函数的定义域关于坐标原点对称，则这个函数为奇函数
B．若一个函数为偶函数，则它的定义域关于坐标原点对称
C．若一个函数的定义域关于坐标原点对称，则这个函数为偶函数
D．若函数f(x)的定义域为，且，则是奇函数
2.定义在(－1,1)上的奇函数f(x)＝，则常数m、n的值分别为________．
3.函数的大致图象是（ ）
A．B．
C．D．
4.已知定义域为R的函数满足：对任意，恒成立，则函数（ ）
A．是奇函数B．是偶函数
C．既是奇函数又是偶函数D．既不是奇函数又不是偶函数
5.若函数的图象关于点对称，则（ ）
A．为偶函数B．为偶函数C．为奇函数D．为奇函数
6.．是R上的奇函数，当时，，则时，（ ）
A．B．
C．D．
7.已知函数为奇函数，为偶函数，且，则（ ）
A．3B．4C．5D．6
8.设是定义域为的奇函数，是偶函数.若，则（ ）
A．-1B．C．1D．
9.已知是定义域为R的奇函数，满足，若，则（ ）
A．2B．C．0D．2022
10.设是定义在R上的奇函数，且当时，，则的解集为（ ）
A．B．
C．D．
11.．已知是定义在上的奇函数，当时，，若，则实数的取值范围是______.
12.已知函数上上单调递减，且对任意实数，都有.若，则满足的的取值范围是
A．B．C．D．
13.已知是定义在上的奇函数，当时，，若存在实数，使在上的值域为，则的值为（ ）
A．B．
C．或D．或
14.已知定义在R上的函数满足，且是奇函数，则（ ）
A．是偶函数B．的图象关于直线对称
C．是奇函数D．的图象关于点对称
培优第二阶——能力提升练
1.下列命题正确的是（ ）
A．奇函数的图象关于原点对称，且
B．偶函数的图象关于y轴对称，且
C．存在既是奇函数又是偶函数的函数
D．奇､偶函数的定义域可以不关于原点对称
2.若函数为奇函数，则（ ）
A．1B．2C．3D．
3.已知函数，则的大致图象为（ ）
A．B．
C．D．
4.已知函数的定义域为，且对任意非零实数，都满足，则（ ）
A．（1）且为偶函数
B．且为奇函数
C．为增函数且为奇函数
D．为增函数且为偶函数
5.设函数，则下列函数中为奇函数的是（ ）
A．B．
C．D．
6..已知是定义在R上的偶函数，当时，，则函数在R上的解析式是
A．B．
C．D．
7..已知，分别是定义在上的偶函数和奇函数，且，则（ ）
A．B．2C．1D．3
8.已知函数和均为上的奇函数，且，，则的值为（ ）
A．B．C．D．6
9.设的定义域为，是奇函数，是偶函数，则（ ）
A．－4B．0C．4D．不确定
10.已知函数是上的偶函数，当时，则不等式的解集是（ ）
A．B．C．D．
11.为定义在R上的奇函数，当时，，若对一切成立.则实数a的取值范围是______.
12.已知定义在R上的奇函数f（x），且对任意实数x1，x2，x1≠x2时，都有（f（x1）﹣f（x2））•（x1﹣x2）＜0．若存在实数x∈[﹣3，3]，使得不等式f（a﹣x）+f（a2﹣x）＞0成立，则实数a的取值范围是（ ）
A．（﹣3，2）B．[﹣3，2]C．（﹣2，1）D．[﹣2，1]
13.偶函数的定义域为，则的最小值
A．-3B．3C．-8D．8
14.函数的定义域为，若是奇函数，是偶函数，则（ ）
A．是奇函数B．是偶函数
C．D．
培优第三阶——培优拔尖练
1..已知上函数 ，则“”是“函数为奇函数”的（ ）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
2.设.若函数，的定义域是.则下列说法错误的是
A．若，都是增函数，则函数为增函数
B．若，都是减函数，则函数为减函数
C．若，都是奇函数，则函数为奇函数
D．若，都是偶函数，则函数为偶函数
3.奇函数，，当时，，则函数的图为（ ）
A．B．C．D．
4.已知函数对任意的实数，，都有，且.则此函数一定（ ）
A．是奇函数B．是偶函数
C．函数图象关于直线对称D．函数图象关于点对称
5.已知函数，且，则满足条件的所有整数的和是______.
6.已知是定义在上的偶函数，且恒成立，当时，，则当时，（ ）
A．B．
C．D．
7.已知，分别是定义在上的偶函数和奇函数，且，则（ ）
A．B．4C．D．8
8.．已知函数为奇函数，且，则（ ）
A．-2B．-5C．-1D．-3
9.我们知道：的图象关于原点成中心对称图形的充要条件是为奇函数，有同学发现可以将其推广为：的图像关于成中心对称图形的充要条件是为奇函数，若的对称中心为，则（ ）
A．B．C．8084D．8086
10.．已知函数是定义在R上的偶函数，且在单调递减，，则的解集为（ ）
A．B．
C．D．
11.．是定义在上的偶函数，且时，，若对任意的 ，不等式恒成立，则实数的取值范围是_______.
12.设函数在（，+）上有意义，对任意的x，y∈R且x≠y，都有