
新高一预习:题型分类细讲精练15 对数函数性质综合应用(人教数学A版2019必修第一册)
展开目录
TOC \ "1-1" \h \u \l "_Tc2465" 【题型一】对数函数绝对值f(x)=|lgax| PAGEREF _Tc2465 1
\l "_Tc20770" 【题型二】 对数函数性质1:真数无理型奇偶性 PAGEREF _Tc20770 2
\l "_Tc6918" 【题型三】对数函数性质2:真数反比例型奇偶性 PAGEREF _Tc6918 3
\l "_Tc8343" 【题型四】对数函数性质3:指对混合型奇偶函数 PAGEREF _Tc8343 3
\l "_Tc22749" 【题型五】对数函数性质4:指对混合型对称中心在y轴 PAGEREF _Tc22749 4
\l "_Tc15631" 【题型六】对数函数性质5:指对混合型中心对称 PAGEREF _Tc15631 5
\l "_Tc29083" 【题型七】对数函数恒成立求参 PAGEREF _Tc29083 5
\l "_Tc22525" 【题型八】对数函数最值型 PAGEREF _Tc22525 6
\l "_Tc25202" 【题型九】对数函数的零点 PAGEREF _Tc25202 6
\l "_Tc27952" 【题型十】对数应用:构造函数 PAGEREF _Tc27952 6
\l "_Tc26067" 培优第一阶——基础过关练 PAGEREF _Tc26067 7
\l "_Tc11205" 培优第二阶——能力提升练 PAGEREF _Tc11205 8
\l "_Tc6923" 培优第三阶——培优拔尖练 PAGEREF _Tc6923 9
【题型一】对数函数绝对值f(x)=|lgax|
【典例分析】
函数,若,,则的范围是( )
A.B.C.D.
【变式训练】
1.已知函数,若有四个不同的解,且,则的最小值________
2.设函数,若关于的方程有四个实数解,,,,且,则的取值范围是__________.
3.已知定义在上的函数,设为三个互不相同的实数,满足,则的取值范围为_______.
【题型二】 对数函数性质1:真数无理型奇偶性
【典例分析】
设函数,若对任意的,不等式恒成立,则a的取值范围是_______.
【变式训练】
1.若函数为定义域上的奇函数,则实数的值为______.
2.若函数为奇函数,则满足的的取值范围是___________.
3.已知函数,若对任意的正数,满足,则_________.
【题型三】对数函数性质2:真数反比例型奇偶性
【典例分析】
设函数是定义在区间上的奇函数(,),则实数n取值范围为______.
【变式训练】
1.知函数,若是奇函数,则实数a=______.
2.关于函数,下列说法错误的是( )
A.定义域为B.图象关于轴对称
C.图象关于原点对称D.在内单调递增
3.若函数是奇函数,则___________,___________.
【题型四】对数函数性质3:指对混合型奇偶函数
【典例分析】
已知函数,则使不等式成立的的取值范围是_______________
【变式训练】
1.已知定义在上的函数,若对任意的,不等式恒成立,则实数的取值范围是__________.
2.已知函数,若,则实数x的取值范围是___________.
3.已知函数为R上的偶函数,则实数___________.
【题型五】对数函数性质4:指对混合型对称中心在y轴
【典例分析】
已知函数,若,则______.
【变式训练】
1..已知函数,则的值为( )
A.B.1C.2D.
2.已知函数,(a,b为常数,且),,则的值是( )
A.8B.4C.D.与a,b有关的数
3.已知函数,若,则________;
【题型六】对数函数性质5:指对混合型中心对称
【典例分析】
已知函数在上的最大值与最小值分别为和,则函数的图象的对称中心是___________.
【变式训练】
1.函数在区间上的最大值与最小值之和为( )
A.1B.C.2D.e
2.已知函数,若、,,则( )
A.B.C.D.
3.已知函数,则( )
A.0B.1C.2D.4
【题型七】对数函数恒成立求参
【典例分析】
已知函数在上恒正,则实数的取值范围是__________.
【变式训练】
1.当时,不等式且恒成立,则实数的取值范围是__________
2.已知,若对恒成立,则实数___________.
3.若不等式对任意的正整数恒成立,则的取值范围是___________.
【题型八】对数函数最值型
【典例分析】
已知函数,若对任意恒有,则的最大值为___________.
【变式训练】
1.函数的最小值为______.
2.已知,,若,则的最大值为( )
A.1B.C.D.0
3.函数的最小值为( )
A.1B.C.D.
【题型九】对数函数的零点
【典例分析】
已知函数若关于的方程有两个不相等的实根,则实数的取值范围是_________.
【变式训练】
1.函数,若关于的方程有个不相等的实数根,则的取值范围是______.
2.已知定义在上的偶函数的图象关于点对称,且当时,,若关于的方程恰好有个不同的实数根,则实数的取值范围是______ .
3.已知关于的方程的两个实数根分别是、,若,则的取值范围为________.
【题型十】对数应用:构造函数
【典例分析】
若正数,满足,,则=________
【变式训练】
1.已知函数的定义域为R,对任意,有,且,则不等式的解集为________.
2.已知函数是奇函数,当时,,若不等式 且对任意的恒成立,则实数的取值范围是____
3.已知函数,则使得不等式成立的x的取值范围是___________.
分阶培优练
培优第一阶——基础过关练
1.已知,则满足的关系式是
A.,且B.,且
C.,且D.,且
2.设命题,;命题当时,解集为,下列命题为真命题的是( )
A.B.C.D.
3.已知函数,则函数的最小值为( )
A.B.C.D.
4.已知函数,若对任意的,存在,使得,则实数的取值范围是( )
A.B.C.D.
5.已知是定义在R上的奇函数,且.当时,,则( )
A.B.C.D.
6.设函数是奇函数,则实数的值等于( )
A.B.1C.D.以上都不对
7.若,则的取值范围为( )
A.B.C.D.
8.若对任意的实数,不等()恒成立,则实数m的取值范围是( )
A.B.C.D.
9.已知函数的值域为R,则a的取值范围是( )
A.B.C.D.
10.已知函数,若,则( )
A.B.C.D.
培优第二阶——能力提升练
1.若正实数满足,则( )
A.B.
C.D.
2.定义在R上的奇函数满足,当时,,则在上( )
A.是减函数,且B.是增函数,且
C.是减函数,且D.是增函数,且
3.已知函数,若实数a满足,则的取值范围是( )
A.B.C.D.
4.已知函数,若关于的不等式的解集为,则实数的取值范围为( )
A.B.C.D.
5.已知函数,则不等式的解集是( )
A.B.
C.D.
6.已知函数,若存在(),使,则的取值范围是______.
7.已知函数对于一切实数均有成立,且,则当,不等式恒成立时,实数的取值范围是__.
8.如图所示,已知函数图像上的两点A,B和函数上的点C,线段AC 平行于y轴,三角形ABC为正三角形时,点B的坐标为,则实数的值为_______________.
9.设,且,函数有最小值,则不等式的解集为____________
10.已知函数,若互不相等,且,则的取值范围是 .
培优第三阶——培优拔尖练
1.已知函数在上的最大值与最小值分别为和,则函数的图象的对称中心是___________.
2.已知函数,若对任意,存在使得恒成立,则实数a的取值范围为____________.
3.已知函数,若(且),则a的取值范围为__________.
4.若不等式对任意的正整数恒成立,则的取值范围是___________.
5.若定义域为的函数满足:对任意能构成三角形三边长的实数,均有,,也能构成三角形三边长,则m的最大值为______.(是自然对数的底)
6.已知,若对恒成立,则实数___________.
7.已知函数,则使不等式成立的的取值范围是_______________
8.已知函数,.设为实数,若存在实数,使得,则的取值范围是___________.
9.已知,且.若函数有最大值,则关于x的不等式的解集为_________.
10.设,则当_______时,取到最大值.
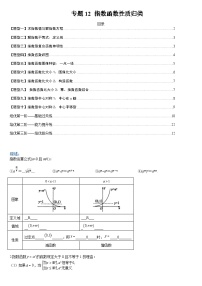
【提分秘籍】
基本规律
对于,若有两个零点,则满足
1.
2.
3.要注意上述结论在对称轴作用下的“变与不变”
【提分秘籍】
基本规律
形如)是奇函数。
【提分秘籍】
基本规律
【提分秘籍】
基本规律
复合型指数函数常见奇偶函数
偶函数:
【提分秘籍】
基本规律
形如
【提分秘籍】
基本规律
形如
新高一预习:题型分类细讲精练21 三角函数性质综合应用(人教数学A版2019必修第一册): 这是一份新高一预习:题型分类细讲精练21 三角函数性质综合应用(人教数学A版2019必修第一册),文件包含专题21三角函数性质综合应用人教A版2019必修第一册解析版docx、专题21三角函数性质综合应用人教A版2019必修第一册原卷版docx等2份试卷配套教学资源,其中试卷共47页, 欢迎下载使用。
新高一预习:题型分类细讲精练19 三角函数图像及性质(人教数学A版2019必修第一册): 这是一份新高一预习:题型分类细讲精练19 三角函数图像及性质(人教数学A版2019必修第一册),文件包含专题19三角函数图像及性质人教A版2019必修第一册解析版docx、专题19三角函数图像及性质人教A版2019必修第一册原卷版docx等2份试卷配套教学资源,其中试卷共64页, 欢迎下载使用。
新高一预习:题型分类细讲精练14 对数函数概念及图像应用归类(人教数学A版2019必修第一册): 这是一份新高一预习:题型分类细讲精练14 对数函数概念及图像应用归类(人教数学A版2019必修第一册),文件包含专题14对数函数概念及图像应用归类人教A版2019必修第一册解析版docx、专题14对数函数概念及图像应用归类人教A版2019必修第一册原卷版docx等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。