2022-2023学年安徽省阜阳市临泉县八年级（下）期末数学试卷（含解析）

这是一份2022-2023学年安徽省阜阳市临泉县八年级（下）期末数学试卷（含解析），共20页。试卷主要包含了选择题，填空题，计算题，解答题，八年级抽取成绩的平均数等内容，欢迎下载使用。
2022-2023学年安徽省阜阳市临泉县八年级（下）期末数学试卷
学校:___________姓名：___________班级：___________考号：___________
第I卷（选择题）
一、选择题（共10小题，共40.0分.）
1. 下列各式计算正确的是(    )
A. B. C. D.
2. 射击时，子弹射出枪口时的速度可用公式进行计算，其中为子弹的加速度，为枪筒的长．如果，，那么子弹射出枪口时的速度用科学记数法表示为(    )
A. B. C. D.
3. 某射击爱好者的次射击成绩单位：环依次为：，，，，，，，，，，则下列结论正确的是(    )
A. 众数是 B. 中位数是 C. 平均数是 D. 方差是
4. 一元二次方程的根的情况是(    )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
5. 在三边分别为下列长度的三角形中，不是直角三角形的是(    )
A. ，， B. ，， C. ， D. ，，
6. 在下列条件中，能够判定平行四边形为矩形的是(    )
A. B. C. D.
7. 如图，在中，，点，，分别在边，，上，，，则四边形的周长是(    )
A.
B.
C.
D.
8. 李师傅家的超市今年月盈利元，月盈利元．若从月到月，每月盈利的平均增长率都相同，则这个平均增长率是(    )
A. B. C. D.
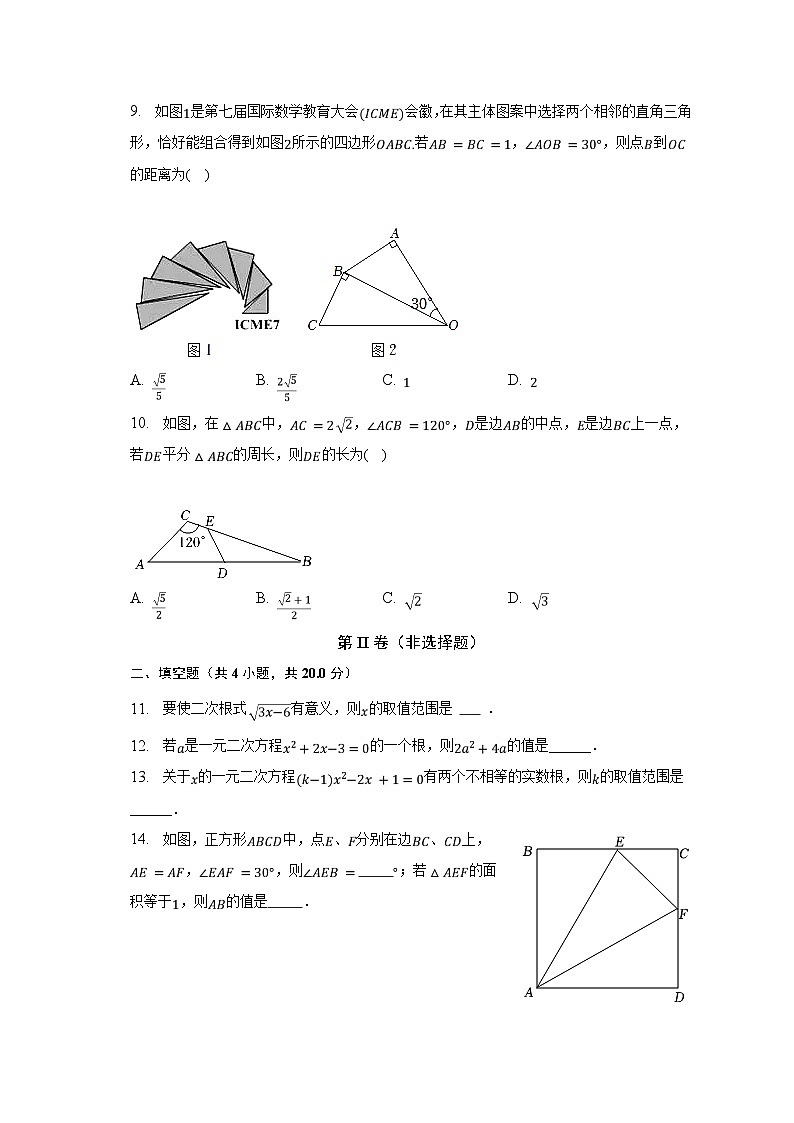
9. 如图是第七届国际数学教育大会会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图所示的四边形若，，则点到的距离为(    )


A. B. C. D.
10. 如图，在中，，，是边的中点，是边上一点，若平分的周长，则的长为(    )


A. B. C. D.
第II卷（非选择题）
二、填空题（共4小题，共20.0分）
11. 要使二次根式有意义，则的取值范围是        ．
12. 若是一元二次方程的一个根，则的值是______．
13. 关于的一元二次方程有两个不相等的实数根，则的取值范围是______．
14. 如图，正方形中，点、分别在边、上，，，则          ；若的面积等于，则的值是          ．


三、计算题（共1小题，共8.0分）
15. 解方程：．
四、解答题（共8小题，共82.0分。解答应写出文字说明，证明过程或演算步骤）
16. 本小题分
计算：．
17. 本小题分
如图，在四边形中，与交于点，，，垂足分别为点，，且，求证：四边形是平行四边形．

18. 本小题分
若的整数部分为，小数部分为，求代数式的值．
19. 本小题分
如图，四边形是菱形，于点，于点．
求证：≌；
若，，求菱形的边长．

20. 本小题分
北京冬奥会期间，某网店直接从工厂购进、两款冰墩墩钥匙扣，进货价和销售价如下表：注：利润销售价进货价
类别价格
款钥匙扣
款钥匙扣
进货价元件


销售价元件


网店第一次用元购进、两款钥匙扣共件，求两款钥匙扣分别购进的件数？
冬奥会临近结束时，网店打算把款钥匙扣调价销售，如果按照原价销售，平均每天可售件经调查发现，每降价元，平均每天可多售件，将销售价定为每件多少元时，才能使款钥匙扣平均每天销售利润为元？
21. 本小题分
某校举办以年北京冬奥会为主题的知识竞赛，从七年级和八年级各随机抽取了名学生的竞赛成绩进行整理、描述和分析，部分信息如下：
：七年级抽取成绩的频数分布直方图如图．
数据分成组，，，，，

：七年级抽取成绩在这一组的是：
，，，，，，，，
，，，，，，，．
：七、八年级抽取成绩的平均数、中位数如下：
年级
平均数
中位数
七年级


八年级


请结合以上信息完成下列问题：
七年级抽取成绩在的人数是______，并补全频数分布直方图；
表中的值为______；
七年级学生甲和八年级学生乙的竞赛成绩都是，则______填“甲”或“乙”的成绩在本年级抽取成绩中排名更靠前；
七年级的学生共有人，请你估计七年级竞赛成绩分及以上的学生人数．
22. 本小题分
阅读材料：
材料：若关于的一元二次方程的两个根为，，则有，．
材料：已知一元二次方程的两个实数根分别为，求的值．
解：方程的两个实数根分别为，，则，，
．
根据上述材料，结合你所学的知识，完成下列问题：
材料理解：若一元二次方程的两个实数根分别为，，则 ______ ， ______ ；
类比应用：已知一元二次方程的两个实数根分别为，，求的值；
思维拓展：已知实数，满足，，且，求的值．
23. 本小题分
如图，将矩形沿对角线折叠，点的对应点为点与交于点．
求证：≌；
若，求的度数；
若，，求的面积．


答案和解析

1.【答案】 
解：、与不属于同类二次根式，不能运算，故A不符合题意；
B、，故B不符合题意；
C、，故C不符合题意；
D、，故D符合题意；
故选：．
利用二次根式的加减法的法则，二次根式的乘除法的法则对各项进行运算即可．
本题主要考查二次根式的混合运算，解答的关键是对相应的运算法则的掌握．

2.【答案】 
解：，
故选：．
把，代入公式，再根据二次根式的性质化简即可．
此题主要考查了科学记数法的表示方法．科学记数法的表示形式为的形式，其中，为整数，表示时关键要正确确定的值以及的值．

3.【答案】 
解：、出现了次，出现的次数最多，该组成绩的众数是，故本选项不符合题意；
B、该组成绩的中位数是，故本选项不符合题意；
C、该组成绩，故本选项符合题意；
D、该组成绩数据的方差，故本选项不符合题意；
故选：．
根据众数、中位数、平均数和方差的定义分别对每一项进行分析，即可得出答案．
此题考查了平均数、中位数、众数和方差的定义，解题的关键是正确理解各概念的含义．

4.【答案】 
解：，
一元二次方程有两个不相等的实数根，
故选：．
求出判别式，判断符号即可得出结论．
本题主要考查了一元二次方程根的判别式，掌握一元二次方程根的判别式时，方程有两个不相等的实数根是解决问题的关键．

5.【答案】 
解：、，，
，
长为，，的三边能组成直角三角形，不符合题意；
B、，，
，
长为，，的三边能组成直角三角形，不符合题意；
C、，，
，
长为，，的三边能组成直角三角形，不符合题意；
D、，，，
，
长为，，的三边不能组成直角三角形，符合题意．
故选：．
求出较小的两条边的平方和，将其与最大的边的平方比较，选其不等的选项即可得出结论．
本题考查了勾股定理的逆定理，牢记“如果三角形的三边长，，满足，那么这个三角形就是直角三角形”是解题的关键．

6.【答案】 
解：、，不能判定平行四边形为矩形，不符合题意；
B、，不能判定平行四边形为矩形，不符合题意；
C、，不能判定平行四边形为矩形，不符合题意；
D、，平行四边形为矩形，符合题意；
故选：．
由平行四边形的判定方法和矩形的判定方法，即可得出结论．
本题考查了矩形的判定方法、平行四边形的判定方法；熟练掌握矩形的判定方法，并能进行推理论证是解决问题的关键．

7.【答案】 
解：，，
四边形是平行四边形，，，
，
，
，，
，，
四边形的周长，
四边形的周长，
，
四边形的周长，
故选：．
由，，得四边形是平行四边形，，，再由和等量代换，即可求得四边形的周长．
本题考查平行四边形的判定与性质、等腰三角形的性质、平行线的在等知识，熟练掌握平行四边形的判定与性质是解题的关键．

8.【答案】 
【解析】
【分析】
此题主要考查了一元二次方程的应用，属于增长率的问题，增长率增长数量原数量如：若原数是，每次增长的百分率为，则第一次增长后为；第二次增长后为，即原数增长百分率后来数．
设该商店的月平均增长率为，根据等量关系：月份盈利额增长率月份的盈利额列出方程求解即可．
【解答】
解：设从月到月，每月盈利的平均增长率为，由题意可得：
，
解得：，舍去，
答：每月盈利的平均增长率为．
故选B．  
9.【答案】 
解：作于，

，，
，
在中，由勾股定理得，
，
，
，
，
，
，
，
故选：．
作于，利用含角的直角三角形的性质得，再由勾股定理得，再根据，得，代入计算可得答案．
本题主要考查了勾股定理，含角的直角三角形的性质，三角函数等知识，熟练掌握等角的三角函数值相等是解题的关键．

10.【答案】 
解：延长至，使，连接，

，
，
为等边三角形，
，
平分的周长，
，
，
，
，
故选：．
延长至，使，连接，根据等边三角形的性质求出，根据三角形中位线定理解答即可．
本题考查的是三角形中位线定理、等边三角形的判定和性质，正确作出辅助线是解题的关键．

11.【答案】 
解：由题意得：，
解得：，
故答案为：．
根据二次根式有意义的条件列出不等式，解不等式得到答案．
本题考查的是二次根式有意义的条件，掌握二次根式的被开方数是非负数是解题的关键．

12.【答案】 
解：是一元二次方程的一个根，
，
，
，
故答案为：．
将代入，即可得出，再把整体代入，即可得出答案．
本题考查了一元二次方程的根的定义，整体思想的应用是本题的关键．

13.【答案】且 
解：根据题意得且，
解得且，
所以的取值范围是且．
故答案为：且．
根据一元二次方程解的定义和根的判别式的意义得到且，然后求出两不等式的公共部分即可．
本题考查了一元二次方程概念和根的判别式：一元二次方程的根与有如下关系：当时，方程有两个不相等的实数根；当时，方程有两个相等的实数根；当时，方程无实数根．

14.【答案】

 
【解析】
【分析】
本题主要考查了正方形的性质，解直角三角形，以及全等三角形的判定和性质，掌握正方形的性质及直角三角形的边角间关系是解决本题的关键．
利用“”先说明与全等，得结论，再利用角的和差关系及三角形的内角和定理求出；先利用三角形的面积求出，再利用直角三角形的边角间关系求出．
【解答】
解：四边形是正方形，
，．
在和中，
，
≌．
．


．
．
过点作，垂足为，如图．

，
．
，
．
即．
．
在中，
，


．
故答案为：；．  
15.【答案】解：将原方程左边分解因式，得
，
 或，
 ，． 
【解析】
【分析】
先将原方程左边分解因式，即可得出两个一元一次方程，求出两个一元一次方程的解即可．
【点评】
本题考查了解一元二次方程因式分解法，把一元二次方程转化成一元一次方程是解此题的关键．  
16.【答案】解：原式


． 
【解析】直接利用二次根式的混合运算法则分别计算，进而得出答案．
此题主要考查了二次根式的混合运算，正确掌握相关运算法则是解题关键．

17.【答案】证明：，
．
．
在与中，
．
≌．
．
四边形是平行四边形． 
【解析】结合已知条件推知；然后由全等三角形的判定定理证得≌，则其对应边相等：；最后根据“对边平行且相等是四边形是平行四边形”证得结论．
本题主要考查了平行四边形的判定：两组对边分别平行的四边形是平行四边形；两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形．

18.【答案】解：，
，
，
的整数部分，小数部分，


． 
【解析】根据算术平方根的定义估算无理数的大小，确定、的值，再代入计算即可．
本题考查估算无理数的大小，掌握算术平方根的定义是正确解答的前提，确定、的值是正确解答的关键．

19.【答案】证明：四边形是菱形，
，，
，，
，
在和中，
，
≌；
解：设菱形的边长为，
，，
，
≌，
，
在中，根据勾股定理得，
，
即，
解得，
菱形的边长是． 
【解析】由菱形的四条边相等、对角相等的性质知，；然后根据已知条件“，”知；最后由全等三角形的判定定理证明≌；
由全等三角形≌的对应边相等知，然后根据菱形的四条边相等求得，设，已知，则，利用勾股定理即可求出菱形的边长．
本题考查了菱形的性质，解题的关键熟记菱形的性质并灵活运用．菱形的性质菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；菱形是轴对称图形，它有条对称轴，分别是两条对角线所在直线．

20.【答案】解：设购进件款钥匙扣，件款钥匙扣，
根据题意得：，
解得：．
答：购进件款钥匙扣，件款钥匙扣；
设将销售价定为每件元，则每件的销售利润为元，平均每天可售出件，
根据题意得，
整理得：，
解得：，．
答：将销售价定为每件元或元时，才能使款钥匙扣平均每天销售利润为元． 
【解析】设购进件款钥匙扣，件款钥匙扣，利用进货总价进货单价进货数量，结合“网店用元购进、两款钥匙扣共件”，可列出关于，的二元一次方程组，解之即可得出结论；
设将销售价定为每件元，则每件的销售利润为元，平均每天可售出件，利用总利润每件的销售利润日销售量，可列出关于的一元二次方程，解之即可得出结论．
本题考查了二元一次方程组的应用以及一元二次方程的应用，解题的关键是：找准等量关系，正确列出二元一次方程组；找准等量关系，正确列出一元二次方程．

21.【答案】解：．
频数直方图如图所示：

 ；
 甲；
人，
即估计七年级竞赛成绩分及以上的学生人数为． 
【解析】
【分析】
本题考查频数分布直方图、用样本估计总体、中位数的意义及求法，理解各个统计量的意义，明确各个统计量的特点是解决问题的前提和关键．
根据各组人数求出的人数，并补全频数分布直方图；
根据中位数的定义求解即可；
根据该学生的成绩大于七年级的中位数，而小于八年级的中位数，即可判断；
用乘样本中竞赛成绩分及以上人数所占比例可得．
【解答】
解：成绩在的人数为人
成绩在的人数为人，
故答案为：，补全频数分布直方图见答案；
第，名学生的成绩分别为，，所以，
故答案为：；
大于七年级的中位数，而小于八年级的中位数．
甲的成绩在本年级抽取成绩中排名更靠前；
故答案为：甲；
见答案．  
22.【答案】   
解：一元二次方程的两个实数根分别为，，
，．
故答案为：，；
一元二次方程的两个实数根分别为，，
，，
；
实数，满足，，且，
，是关于的一元二次方程的两个实数根，
，，
．
利用根与系数的关系，可求出及的值；
利用根与系数的关系，可得出，，再将其代入中，即可求出结论；
由实数，满足的条件，可得出，是关于的一元二次方程的两个实数根，利用根与系数的关系，可得出，，再将其代入中，即可求出结论．
本题考查了根与系数的关系以及分式的化简求值，牢记“关于的一元二次方程的两根之和等于，两根之积等于”是解题的关键．

23.【答案】证明：将矩形沿对角线折叠，
则，．
在和中，
，
≌．
≌，
，
四边形是矩形，
，
，
，
．
 ≌，
，
设，
四边形是矩形，
，
，
在中，
，
，
解得，
． 
【解析】由矩形与折叠的性质可得，，从而可得结论；
先证明，再求解，结合对折的性质可得答案．根据全等三角形的性质得，然后在中，由勾股定理列方程求得的长，再由的面积即可求解．
本题考查的是全等三角形的判定与性质，轴对称的性质，矩形的性质，熟练的运用轴对称的性质证明边与角的相等是解本题的关键．