山东省德州市平原县2021-2022学年八年级下学期期末考试数学试卷(含解析)

这是一份山东省德州市平原县2021-2022学年八年级下学期期末考试数学试卷(含解析)，共18页。试卷主要包含了某市6月份某周气温，下列命题的逆命题成立的是等内容，欢迎下载使用。
2021-2022学年第二学期八年级期末测试
数学试题
本试题分选择题，48分；非选择题，102分；全卷满分150分，考试时间120分钟。
注意事项：
1．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、准考证号填写在答题卡规定的位置上。
2．第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮换干净后，再涂其他答案标号。
3．第Ⅱ卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内的位置，不能写在在试卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不能用涂改液、胶带纸、修正带。不按要求作答的答案无效。
4．填空题请直接填写答案，解答题应写出文字说明、证明过程或演算步骤。
第Ⅰ卷（选择题 共计48分）
一、选择题（本大题共12个小题每小题4分，共48分。在每小题给出的四个选项中，只有一项是符合题目要求的）
1．下列各式中：，其中是二次根式的有（    ）
A．1个 B．2个 C．3个 D．4个
2．以下列各组数据为三角形三边，能构成直角三角形的是(   )
A．4cm，8cm，7cm B．3 cm，5 cm，2 cm
C．2 cm，2 cm，4 cm D．13 cm ，12 cm ，5 cm
3．不能判定一个四边形是平行四边形的条件是（　　）．
A．两组对边分别平行 B．一组对边平行，另一组对边相等
C．一组对边平行且相等 D．两组对边分别相等
4．下列关于x的方程是一元二次方程的是　　
A． B．
C． D．
5．某市6月份某周气温（单位：℃）为23、25、28、25、28、31、28，则这组数据的众数和中位数分别是（　　）
A．25、25 B．28、28 C．25、28 D．28、31
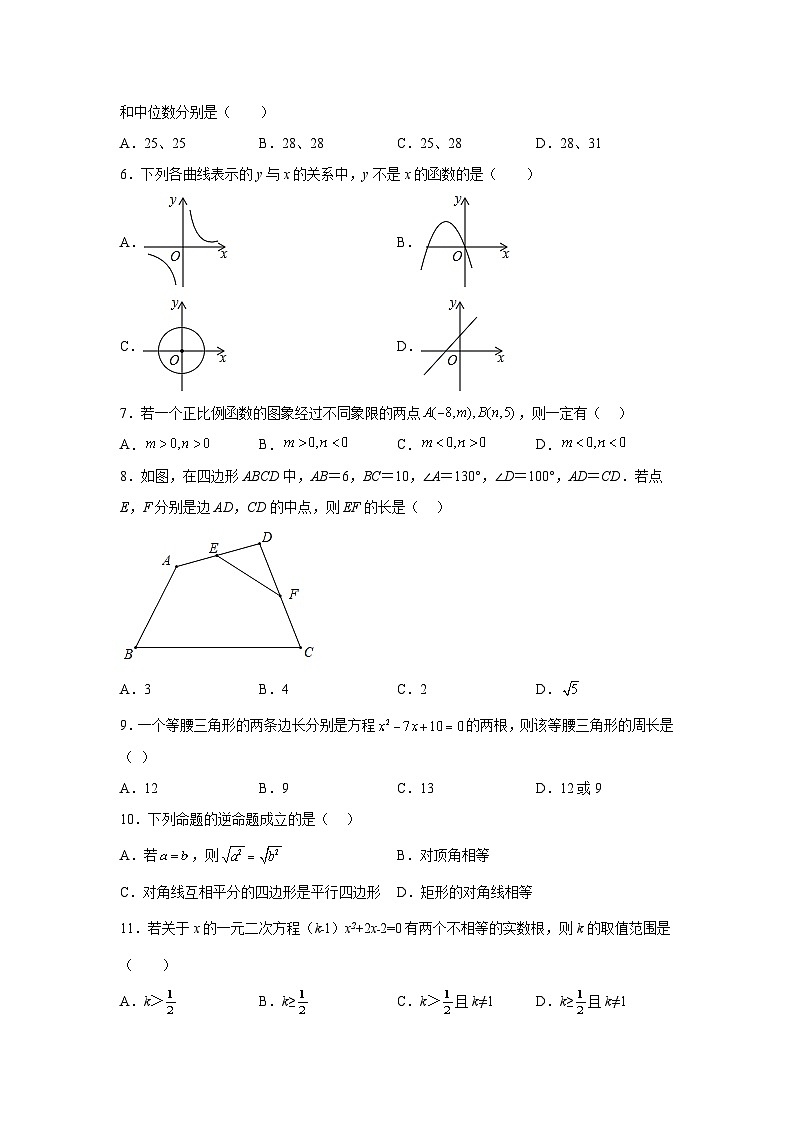
6．下列各曲线表示的y与x的关系中，y不是x的函数的是（　　）
A． B．
C． D．
7．若一个正比例函数的图象经过不同象限的两点，则一定有（    ）
A． B． C． D．
8．如图，在四边形ABCD中，AB＝6，BC＝10，∠A＝130°，∠D＝100°，AD＝CD．若点E，F分别是边AD，CD的中点，则EF的长是（    ）

A．3 B．4 C．2 D．
9．一个等腰三角形的两条边长分别是方程的两根，则该等腰三角形的周长是（ ）
A．12 B．9 C．13 D．12或9
10．下列命题的逆命题成立的是（    ）
A．若，则 B．对顶角相等
C．对角线互相平分的四边形是平行四边形 D．矩形的对角线相等
11．若关于x的一元二次方程（k﹣1）x2+2x﹣2=0有两个不相等的实数根，则k的取值范围是（　　）
A．k＞ B．k≥ C．k＞且k≠1 D．k≥且k≠1
12．如图3，在中，按如下步骤作图：①以A为圆心，长为半径画弧交于F；②连接，分别以点B，F为圆心，以大于的长为半径作弧，两弧交于点G；③作射线交于点E，若，则的长为（    ）

A．8 B．7 C．6 D．5
第Ⅱ卷（非选择题 共102分）
二、填空题（本大题共6小题，每小题填对得4分，共24分，只要求填写最后结果）
13．若代数式有意义，则x的取值范围是__________．
14．某种药原来每瓶售价为40元，经过两次降价，现在每瓶售价为25.6元，若设平均每次降低的百分率为，根据题意列出方程为______________________．
15．如图，一架云梯长米，斜靠在一面墙上，梯子顶端离地面米，要使梯子顶端离地面米，则梯子的底部在水平面方向要向左滑动______米．

16．如图，在四边形ABCD中，AD//BC，在不添加任何辅助线的情况下，请你添加一个条件____，使四边形ABCD是平行四边形（填一个即可）．

17．已知正比例函数的图象过点(2，4)．把该函数图象平移，使它过点(1，−1)，则平移后所得函数的解析式是________．
18．如图，在正方形中，对角线与交于点，点在的延长线上，连接，点是的中点，连接交于点．若，，则点到的距离为__________．

三、解答题（本大题共7小题，共78分）
19．（1）计算：；
（2）解一元二次方程：
20．为宣传防护知识，增强免疫能力，某校开展了“防疫知识测试”活动，并随机抽取了名学生的测试成绩如下(单位：分)：，，整理上边的数据得到如下频数分布直方表和频数分布直方图：
成绩（分）
频数

4









根据图表回答下列问题
（1）抽取的个数据中，中位数是 ；频数分布表中 ；
（2）补全频数分布直方图；
（3）若测试成绩不低于分为优秀，则估计该校名学生中，达到优秀等级的人数有多少？
21．如图，一次函数的图象与x轴相交于点B，与过点的一次函数的图象相交于点．

(1)求一次函数图象相应的函数表达式；
(2)求的面积．
22．利客来超市销售某种商品，平均每天可售出20件，每件盈利40元，为了扩大销售，增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低2元，平均每天可多售出4件．
（1）若降价6元，则平均每天销售数量为　 　件；
（2）当每件商品降价多少元时，该商店每天销售利润为1200元？
23．如图，四边形是矩形．

(1)在图1中作对角线的垂直平分线，分别交于点M、N，垂足为点O（要求用尺规作图，保留作图痕迹，不要求写作法）
(2)在（1）中，连接和，求证：四边形是菱形；
(3)如图2，点E在矩形的边上，且，延长到点F，使，连接．若，，则四边形的面积为多少？
24．斌斌同学根据学习函数的经验，对函数的图像和性质进行了探究．下面是斌斌的探究过程，请解决相关问题．
(1)列表、描点、画出图像．
①把下表补充完整：
x
…




0
1
2
3
4
…
y
…


1
3
5
3



…
②如图，描出以表中各对对应值为坐标的剩余的两个点，并画出该函数的图像．

(2)观察的图像，下列说法正确的是___________（填序号，可多选）．
①若点在图像上，则；
②函数有最大值，最大值是5；
③函数的图像是轴对称图形，对称轴是y轴；
④y随x的增大而增大．
(3)画出一次函数的图像，并利用图像法直接写出不等式的解集．
25．（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE，求证：CE＝CF；
（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，请你利用（1）的结论证明：GE＝BE＋GD；
（3）运用（1）（2）解答中所积累的经验和知识，完成下题：
如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC，E是AB上一点，且∠DCE＝45°，BE＝4，DE=10, 求直角梯形ABCD的面积．











1．B
解析：解：a＜0时，无意义，不是二次根式；和是二次根式；不是二次根式；x＋2＜0时，无意义，不是二次根式；
故选：B．
2．D
解析：解：A、42+72≠82，故不为直角三角形；
B、22+32≠52，故不为直角三角形；
C、2+2=42，故不能构成三角形，不能构成直角三角形；
D、52+122=132，故构成直角三角形．
故答案为D．
3．B
解析：∵①两组对边分别平行的四边形是平行四边形；②两组对边分别相等的四边形是平行四边形；③两组对角分别相等的四边形是平行四边形；④对角线互相平分的四边形是平行四边形；⑤一组对边平行且相等的四边形是平行四边形．
∴ A、D、C均符合是平行四边形的条件，B则不能判定是平行四边形．
故选B．
4．C
解析：A、是一元一次方程，故A不符合题意；
B、时是一元一次方程，故B不符合题意；
C、是一元二次方程，故C符合题意；
D、是二元二次方程，故D不符合题意；
故选C．
5．B
解析：将这组数据按从小到大的顺序排列23，25，25，28，28，28，31，
在这一组数据中28是出现次数最多的，故众数是28℃．
处于中间位置的那个数是28，那么由中位数的定义可知，这组数据的中位数是28℃；
故选B．
6．C
解析：根据函数的意义可知：对于自变量x的任何值，y都有唯一的值与之相对应，所以只有选项C不满足条件．
故选C．
7．C
解析：解：A、m＞0，n＞0，A点在第二象限，B点在第一象限，不符合题意，故本选项错误；
B、m＞0，n＜0，A点在第二象限，B点在第二象限，不符合题意，故本选项错误；
C、m＜0，n＞0，A点在第三象限，B点在第一象限，符合题意，故本选项正确；
D、m＜0，n＜0，A点在第三象限，B点在第二象限，不符合题意，故本选项错误．
故选：C．
8．B
解析：解：连接AC，
∵DA＝DC，∠D＝100°，
∴∠DAC＝∠DCA＝40°，
∴∠BAC＝∠BAD﹣∠DAC＝130°﹣40°＝90°，
∴AC＝，
∵点E，F分别是边AD，CD的中点，
∴EF＝AC＝4，
故选：B．

9．A
解析：解：因式分解可得：(x－2)(x－5)=0
解得：，
当2为底，5为腰时，则三角形的周长为2+5+5=12；
当5为底，2为腰时，则无法构成三角形，
故选：A
10．C
解析：解：A、若，则的逆命题是：若，则，不成立，该选项不符合题意；
B、对顶角相等的逆命题是：相等的角是对顶角，不成立，该选项不符合题意；
C、对角线互相平分的四边形是平行四边形的逆命题是：平行四边形的对角线互相平分，成立，该选项符合题意；
D、矩形的对角线相等的逆命题是：对角线相等的四边形是矩形，不成立，该选项不符合题意；
故选：C．
11．C
解析：根据题意得：k-1≠0且△=22-4（k-1）×（-2）＞0，
解得：k＞且k≠1．
故选：C
12．A
解析：解：如图，设AE交BF于点O．

由作图可知：AB＝AF，∠BAE＝∠EAF，
∴OB＝OF，AE⊥BF，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠EAF＝∠AEB，
∴∠BAE＝∠AEB，
∴AB＝BE＝AF，
∵AF∥BE，
∴四边形ABEF是平行四边形，
∵AB＝AF，
∴四边形ABEF是菱形，
∴OA＝OE，OB＝OF＝3，
在Rt△AOB中，∠AOB＝90°，
∴OA＝，
∴AE＝2OA＝8．
故选：A．
13．且
解析：解：∵代数式有意义，
∴，
解得：且，
故答案为：且．
14．
解析：设平均每次降低的百分率为x，根据题意得：40（1﹣x）2=25.6．
故答案为40（1﹣x）2=25.6．
15．
解析：如图，AB=DE=10，AC=6，DC=8，∠C =90°，
∴BC==8，
CE==6，
∴BE=BC-CE=2（米），
故答案为2.

16．AD=BC（答案不唯一）
解析：解：根据一组对边平行且相等的四边形是平行四边形，可以添加条件AD=BC，
根据两组对边分别平行的四边形是平行四边形，可以添加条件AB∥DC，
本题只需添加一个即可，
故答案为：AD=BC（答案不唯一）．
17．
解析：解：把点（2，4）代入y=kx（k≠0）得2k=4，
解得k=2，
∴正比例函数解析式为y=2x，
设正比例函数平移后函数解析式为y=2x+b，
把点（1，-1）代入y=2x+b得-1=2+b，
∴，
∴平移后函数解析式为，
故答案为：．
18．
解析：如图，过点A作AH⊥DF的延长线于点H，
∵在正方形ABCD中，对角线AC与BD交于点O，
∴O为AC中点
∵F点是AE中点，
∴OF是△ACE的中位线，
∴CE=2OF=6
∴G点是AD的中点，
∴FG是△ADE的中位线，
∴GF==1
∴CD=CE-DE=4,
∴AD=CD=4
在Rt△ADE中，AD=4,DE=2
∴AE=
∴DF=AE=
∴S△AFD=AD·GF=FD·AH
即×4×1=××AH
∴AH=
∴点A到DF的距离为，
故答案为：．

19．（1）
（2）x1=-2或x2=8
解析：解：（1）


（2）
，
，
，
x1=-2或x2=8．
20．（1）分，7，6；（2）见解析；（3）1900人
解析：解：（1）抽取的30个数据中，中位数是87分；频数分布表中a=7；b=6；
故答案为：87分，7，6；
（2）如图即为补全的频数分布直方图；

（3）∵随机抽取的30名学生中成绩不低于86分的人数为：11+6+2=19（人），
∴估计该校3000名学生中，达到优秀等级的人数为：（人）．
答：估计该校3000名学生中，达到优秀等级的人数有1900人．
21．(1)；
(2)12
解析：（1）解：（1 ）∵点在一次函数的图象上，
∴，
∴点，
设一次函数图象相应的函数表达式为，
把点，代入得：
，
解得，
∴一次函数图象相应的函数表达式；
（2）解：∵一次函数的图象与x轴交于点B，
∴当时，，解得，
∴，
∵，，
∴，
∴．
22．（1）32；（2）每件商品应降价10元时，该商店每天销售利润为1200元．
解析：解：（1）若降价6元，则平均每天销售数量为20+4×3＝32件．
故答案为32；
（2）设每件商品应降价x元时，该商店每天销售利润为1200元．
根据题意，得 （40﹣x）（20+2x）＝1200，
整理，得x2﹣30x+200＝0，
解得：x1＝10，x2＝20．
∵要求每件盈利不少于25元，
∴x2＝20应舍去，
解得：x＝10．
答：每件商品应降价10元时，该商店每天销售利润为1200元．
23．(1)见解析
(2)见解析
(3)80
（1）解：如图所示，MN即为所求；
（2）证明：连接和，如图所示：∵四边形ABCD为矩形，∴AD∥BC，∴∠ADB＝∠CBD，∵MN垂直平分线段BD，∴BO＝DO，在△DMO和三角形BNO中，，∴△DMO≌△BNO（ASA），∴MO＝NO，∴四边形DMBN是平行四边形，又∵MN⊥BD，∴四边形DMBN是菱形；
（3）在矩形ABCD中，AD＝BC＝10，AD∥BC，∠ABC＝90°，∵，∴FE＝BC，∴AD＝FE＝10，又∵AD∥FE，∴四边形AFED是平行四边形，∴AF＝DE＝AD＝10，∴BF＝FE－BE＝10－4＝6，∵∠ABF＝180°－∠ABC＝90°，∴AB＝，∴四边形的面积＝FE·AB＝10×8＝80．
24．(1)①－1，1；②见解析；
(2)②③；
(3)x≤－3或x≥1．
（1）解：①当x＝－3时，，当x＝2时，，故答案为：－1，1；②描点、连线，函数的图像如图所示：
（2）由函数图像可知：①若点在图像上，则对应的m值有两个，通过计算可得，原说法错误；②函数有最大值，最大值是5，正确；③函数的图像是轴对称图形，对称轴是y轴，正确；④当x＜0时，y随x的增大而增大，当x＞0时，y随x的增大而减小，原说法错误；故答案为：②③；
（3）在中，当x＝0时，y＝2；当y＝0时，x＝－2；∴一次函数的图像过点（0，2），（－2，0），函数图像如图，由函数图像可得，一次函数的图像与函数的图像交于点（－3，－1），（1，3），∴不等式的解集为：x≤－3或x≥1．
25．（1）证明见解析；（2）证明见解析；（3）108.
解析：（1）如图1，在正方形ABCD中，
∵BC=CD，∠B=∠CDF，BE=DF，
∴△CBE≌△CDF，
∴CE=CF；
（2）如图，延长AD至F，使DF=BE，连接CF，

由（1）知△CBE≌△CDF，
∴∠BCE=∠DCF，
∴∠BCE+∠ECD=∠DCF+∠ECD，
即∠ECF=∠BCD=90°，
又∵∠GCE=45°，
∴∠GCF=∠GCE=45°，
∵CE=CF，∠GCE=∠GCF，GC=GC，
∴△ECG≌△FCG，
∴GE=GF，
∴GE=DF+GD=BE+GD；
（3）如图：过点C作CF⊥AD于F，

∵AD∥BC，∠B＝90°，
∴∠A＝90°，
∵∠A＝∠B＝90°，FC⊥AD，
∴四边形ABCF是矩形，且AB＝BC＝12，
∴四边形ABCF是正方形，
∴AF＝12，
由（2）可得DE＝DF＋BE，
∴DE＝4＋DF，
在△ADE中，AE2＋DA2＝DE2，
∴（12−4）2＋（12−DF）2＝（4＋DF）2，
∴DF＝6，
∴AD＝6，
∴S四边形ABCD＝ (AD＋BC)×AB＝×(6＋12)×12＝108．