第六章平面图形的认识小结与思考-（苏科版）课件PPT

这是一份第六章平面图形的认识小结与思考-（苏科版）课件PPT，共23页。

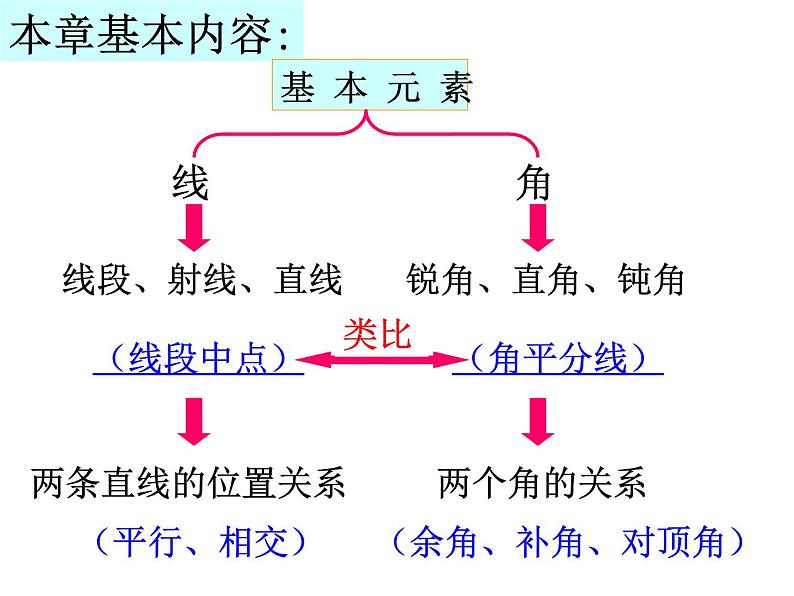
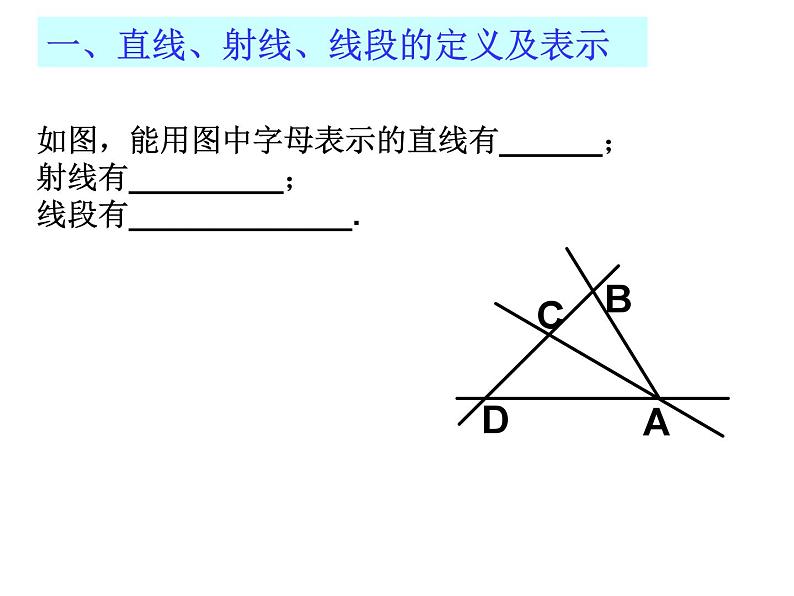
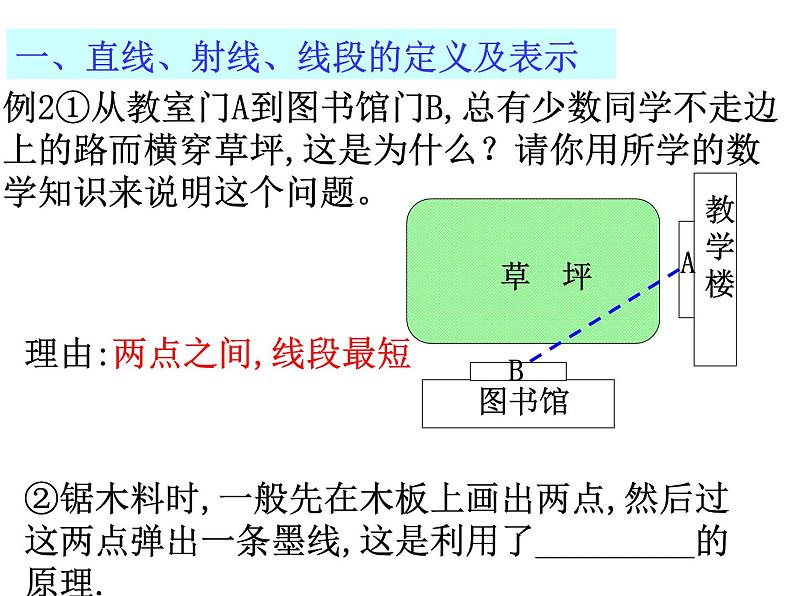
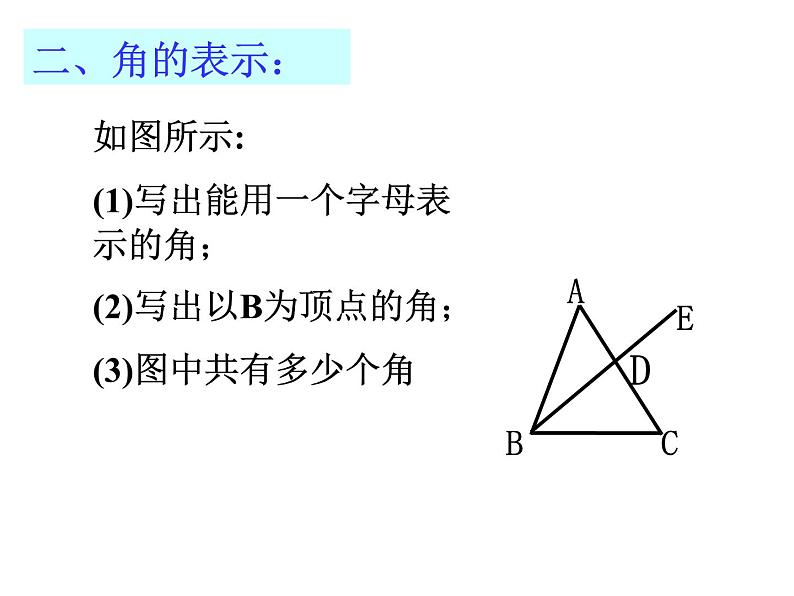
第六章小结与思考线本章基本内容:线段、射线、直线（线段中点）两条直线的位置关系角锐角、直角、钝角（角平分线）两个角的关系类比（平行、相交）（余角、补角、对顶角）基 本 元 素 一、直线、射线、线段的定义及表示如图，能用图中字母表示的直线有______；射线有_________；线段有_____________.一、直线、射线、线段的定义及表示②锯木料时,一般先在木板上画出两点,然后过这两点弹出一条墨线,这是利用了_________的原理.理由:两点之间,线段最短二、角的表示：如图所示:(1)写出能用一个字母表示的角；(2)写出以B为顶点的角；(3)图中共有多少个角14°36′36″= °100.62°= ° ′ ″5°44″＋ 2°59′48″=_______90°－13°30′48″=_________三、角：角的度量单位四、线段中点的定义及性质1、如图，C是AB的中点，D是BC的中点，下面等式中正确的有________①CD=AC－DB ②CD=AD-BC③CD＝ AB－BD ④CD= AB四、线段中点的定义及性质2.已知线段AB=12cm，直线AB上有一点C，且BC=6cm，M是线段AC的中点.则线段AM的长为__________cm.五、角平分线的相关知识：五、角平分线的相关知识：2．若∠AOB=60°，其角平分线为OM，∠BOC=20°，其角平分线为ON，则∠MON=___.六、角的运算14°36′36″= °100.62°= ° ′ ″26°54′+ 53°8′=____________； 60°－21°18′20″=_______________.1.一个角是34.3° ， 则它的余角是_____，它的补角是_______.变式：一个角的补角的余角等于这个角的 ，求这个角的度数. 2、从1点15分到1点30分，时钟的分针与时针各转了多少角度?七、角：生活中特殊角八、距离直线外一点到该直线的垂线段的长度。2.点到直线的距离：1.两点间的距离：两点之间线段的长度。如图，线段AB的长度为点A到点B的距离垂线段OA的长度为点A到直线a的距离3.如图，表示P点到直线a的垂线段PQ的是( ) ABCD课堂练习:4、如图，AC⊥BC，CD⊥AB，垂足分别是C、D. 比较图中线段的大小（填“＞”“＜”或“＝”）（1）CD______AC,理由是____________；（2）BC______AB,理由是____________；（3）CD______AB,理由是____________.P174—T65、如图，CA⊥AB于点A，CD⊥AD于点D：(1)点C到直线AB的距离是__________， 所以BC___CA(比较大小)，理由是___________.35(2)若AD=3,BC=5,则AC有取值范围是_____________.CA的长度＞垂线段最短3＜AC＜51.作线段、射线、直线2.作一角等于已知角(三弧定一线）3.作平行线、垂线、垂线段平行垂直1.过直线外一点有且仅有一条直线与已知直线平行。2.平行于同一条直线的两条直线平行。1. 过一点有且仅有一条直线与已知直线垂直。2.直线外一点与直线上所有点的连线中，垂线段最短。九、作图1.如图，已知四点A、B、C、D，（1）连接AB，画射线DC，射线AD，直线BC；（2）延长线段AB交射线DC于点E；2.已知:∠AOB，求作∠DEF= ∠AOB (用尺规作图,并保留作图痕迹)3. P173—T3九、作图4.如图方格纸中，每个小正方形的边长为1，每个小正方形的顶点都叫做格点. (1)按下列要求画图： 过点C画AB的平行线CD；过点A画AE⊥AB，且AE=AB.(2)三角形ABC的面积为______________. ∵∠1+∠2=90° ∠2+∠3=90°∴∠1=∠3其推理依据是________________∵∠1+∠3=180° ∠2+∠4=180° ∠1=∠2∴∠3=∠4其推理依据是______________十、几何说理：余角、补角、对顶角∵∠1与∠3是对顶角∴∠1=∠3其推理依据是_______同角的余角相等等角的补角相等对顶角相等1、如图，BD平分∠ABC，CE平分∠ACB，∠DBC= ∠ECB. ∠ABC 与∠ACB相等吗？为什么？P177—T82、如图，直线AB与CD相交于点O，OE⊥CD，OF⊥AB，OP平分∠COB，∠DOF=65°，求∠1和∠2的度数.3、如图，OC是∠ AOB内的一条射线，OD、OE平分∠ AOB 、∠ AOC，（1）若∠AOC=30°， ∠BOC=90°，求∠DOE的度数.（2）若∠AOC=m°， ∠BOC=n°，求∠DOE的度数.P178—T13