



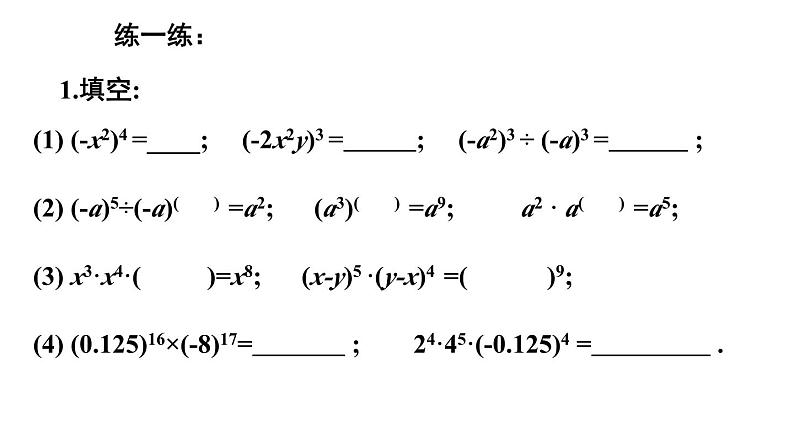


还剩8页未读,
继续阅读
第8章幂的运算复习课件 -(苏教科)
展开
这是一份第8章幂的运算复习课件 -(苏教科),共15页。
七年级(下册)初中数学第八章 小结与复习1.四条法则:知识点回顾: am · an = (m、n是整数); (am)n = (m、n是整数); (ab)n = (n是整数); am÷an = (a≠0,m、n是整数).am+namnanbnam-n2.两个规定: a 0 = (a ≠ 0).13.一个科学记数法:例1:计算:典型例题:(1) (x3)2÷(-x)2·x+ x·(-x)2·(-x2)(2) (b-a)5·(a-b)÷(a-b)3 (3) 0.25 ×0.44 × 12.54解(1)原式=x3×2÷x2 ·x-x1+2+2 =x6-2+1-x5=x5-x5=0(2)原式=-(a-b)5 ·(a-b)÷(a-b)3 =-(a-b)5+1-3=-(a-b)3(3)原式=0.24+1×0.44×12.54 =0.2×0.24×0.44×12.54 =0.2×(0.2×0.4×12.5)4=0.2×1=0.2例2:典型例题:(1)若an = 3, bn = 5 , 求 a3n+b2n 和 a3n·b2n的值.(3)若 2x+3·3x+3 = 36x-2, 求 x 的值.(2)若xn = 3, yn =7, 求 (xy)n 和 (x2y3)n 的值.(4)若x2n = 5, 求 (3x3n)2 - 4(x2)2n 的值. 1.填空:练一练:(3) x3·x4·( )=x8; (x-y)5 ·(y-x)4 =( )9; (1) (-x2)4 =____; (-2x2y)3 = ; (-a2)3 ÷ (-a)3 = ;(2) (-a)5÷(-a)( ) =a2; (a3)( ) =a9; a2 · a( ) =a5;(4) (0.125)16×(-8)17= ; 24·45·(-0.125)4 = . 2.用科学记数法表示下列各数. -2730000, -0.00000000901, 0.00007008.练一练: 3.写出下列各数的原数. 10-3, 1.2×105 , -2.05×10-5 , 1.001÷106.4.已知: 8·22m-1·23m =217,求m的值 .练一练:5.已知:am-n = 7, am+n = 13, 求a2m. 练一练:先化简,再求值:a2·a4+a·[(-a)2]2·a-(2a·a2)3例5:请写出同底数幂的乘法法则推导过程:am·an=a·a·…·a · a·a·…·a= a·a·…·a =am+n练一练:请你写出同底数幂的乘方推理过程 6.如图,将正方形的对边中点连接起来,可以将正方形分成4个形状和面积相同的小正方形,再将其右下角的小正方形对边中点连接起来,又可将这个小正方形分割成4个形状和面积相同的小正方形……如果大正方形边长为1,那么经过10次这样的分割后所得右下角正方形面积是( )C练一练:7.比较340与430的大小.练一练: 8.计算.(1) (-x2y)5÷(-x2y)3 (2) (x-y)8÷(x-y)4÷(y-x)3 (3) (-a10)3÷(-a)10÷(-a3)2 (4) 98×272÷(-3)18课堂小结:通过本节课,你有什么收获?再 见
七年级(下册)初中数学第八章 小结与复习1.四条法则:知识点回顾: am · an = (m、n是整数); (am)n = (m、n是整数); (ab)n = (n是整数); am÷an = (a≠0,m、n是整数).am+namnanbnam-n2.两个规定: a 0 = (a ≠ 0).13.一个科学记数法:例1:计算:典型例题:(1) (x3)2÷(-x)2·x+ x·(-x)2·(-x2)(2) (b-a)5·(a-b)÷(a-b)3 (3) 0.25 ×0.44 × 12.54解(1)原式=x3×2÷x2 ·x-x1+2+2 =x6-2+1-x5=x5-x5=0(2)原式=-(a-b)5 ·(a-b)÷(a-b)3 =-(a-b)5+1-3=-(a-b)3(3)原式=0.24+1×0.44×12.54 =0.2×0.24×0.44×12.54 =0.2×(0.2×0.4×12.5)4=0.2×1=0.2例2:典型例题:(1)若an = 3, bn = 5 , 求 a3n+b2n 和 a3n·b2n的值.(3)若 2x+3·3x+3 = 36x-2, 求 x 的值.(2)若xn = 3, yn =7, 求 (xy)n 和 (x2y3)n 的值.(4)若x2n = 5, 求 (3x3n)2 - 4(x2)2n 的值. 1.填空:练一练:(3) x3·x4·( )=x8; (x-y)5 ·(y-x)4 =( )9; (1) (-x2)4 =____; (-2x2y)3 = ; (-a2)3 ÷ (-a)3 = ;(2) (-a)5÷(-a)( ) =a2; (a3)( ) =a9; a2 · a( ) =a5;(4) (0.125)16×(-8)17= ; 24·45·(-0.125)4 = . 2.用科学记数法表示下列各数. -2730000, -0.00000000901, 0.00007008.练一练: 3.写出下列各数的原数. 10-3, 1.2×105 , -2.05×10-5 , 1.001÷106.4.已知: 8·22m-1·23m =217,求m的值 .练一练:5.已知:am-n = 7, am+n = 13, 求a2m. 练一练:先化简,再求值:a2·a4+a·[(-a)2]2·a-(2a·a2)3例5:请写出同底数幂的乘法法则推导过程:am·an=a·a·…·a · a·a·…·a= a·a·…·a =am+n练一练:请你写出同底数幂的乘方推理过程 6.如图,将正方形的对边中点连接起来,可以将正方形分成4个形状和面积相同的小正方形,再将其右下角的小正方形对边中点连接起来,又可将这个小正方形分割成4个形状和面积相同的小正方形……如果大正方形边长为1,那么经过10次这样的分割后所得右下角正方形面积是( )C练一练:7.比较340与430的大小.练一练: 8.计算.(1) (-x2y)5÷(-x2y)3 (2) (x-y)8÷(x-y)4÷(y-x)3 (3) (-a10)3÷(-a)10÷(-a3)2 (4) 98×272÷(-3)18课堂小结:通过本节课,你有什么收获?再 见
相关资料
更多









