初中数学人教版九年级上册第二十三章 旋转23.2 中心对称23.2.1 中心对称导学案

23.2 中心对称（1）

学习目标：

1、掌握中心对称的定义以及相关概念。理解中心对称的性质，能够利用性质解决相关问题。

2、能够依据中心对称的性质解决相关作图问题。

重点：作图以及利用性质解决问题。

难点：利用性质解决问题。

学习过程：

一、复习旧知：（见课件）

二、自学教材P64-----P65回答下列问题。

1、自学教材P64思考，解答：

把一个图形_______________________                 _________________那么就说这两个图形关于这个点中心对称。这个点叫__       _____。

2、结合中心对称的定义回答：①中心对称的图形有__     __个；

②中心对称是把一个图形绕某一点旋转_      __°

③中心对称揭示了___      __个图形中的一种__     _____关系；对称点的连线被_______   ___平分，即对称点的连线经过___    ______.

三、利用上述性质解答：（可参看教材P65例题）

例(1)已知P点和O点，画出点P关于点O的对称点P'

（2)已知线段AB和O点，画出线段AB关于点O的对称线段A' B'

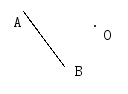
（3）如图，以点O为中心，画出与△ABC关于点O对称的△A′B′C′.

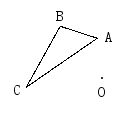
（4）如图，以点O为对称中心，画出与四边形ABCD关于点O对称的四边形A′B′C′D′.

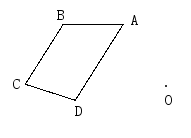
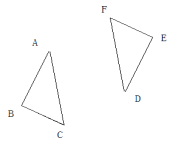
（5）、△ABC与△DEF关于点O中心对称，做出对称点。

四、随堂检测：

1、下列说法错误的是 (   )

A．中心对称图形一定是旋转对称图形  B．轴对称图形不一定是中心对称图形  
C．在成中心对称的两个图形中，连接对称点的线段都被对称中心平分

D．旋转对称图形一定是中心对称图形。
2、关于中心对称的两个图形,对应线段的关系是(     )．
 (A) 平行   (B) 相等   (C) 平行且相等   (D) 相等且平行或在同一直线上

3、关于中心对称的两个图形，对称点的连线____________

4、 如果两个图形的对应点连成的线段都经过某一点，并且被平分，则这两个图形一定关于这一点成____________对称．

 5、ΔABC和ΔA’B’C’关于点O中心对称，若ΔABC的周长为12cm，ΔA’B’C’的面积为6cm2,则ΔA’B’C’的周长为___________，ΔABC的面积为_________。

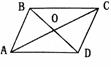6、 如图所示，△ABO与△CDO关于点O成中心对称，则在同一直线上的三点有       ，并且AO＝       ，BO＝         .

7、已知点O是平行四边形 ABCD对角线的交点,则图中关于点O对称的三角形有____对,它们分别是____________________________.     

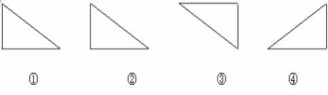
8、右图中②③④⑤分别由①图顺时针旋转180°变换而成的是____________。

9、 在右面四个图形中，图形①与___________成轴对称，图形①与图形___________成中心对称．

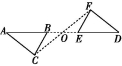
10、互动探究2:如图,△ABC与△DEF关于O点成中心对称,则AB=DE,BC∥　　,

AC=　　,∠ACB=　　. 

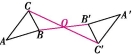
【方法归纳交流】关于中心对称的两个图形,对应线段　　或在同一条直线上且　　. 

11、 如右图所示的四组图形中，左边图形与右边图形成中心对称的有__________组.

12、如图1，等腰梯形ABCD中，AB∥CD，AB=2CD，AC交BD于点O，点E、F分别为AO、BO的中点，则下列关于点O成中心对称的一组三角形是（    ）．

A．  B．   C．   D．

五、回顾本节课，谈谈收获与不足。

1、利用旋转的性质:中心对称的两个图形的对称点到____    __的距离相等，亦即对称点的连线被_______   ___平分，对称点的连线经过___    ______.即        、        三点共线。

2、由旋转的性质:  旋转前后对应的线段______  _____,可知中心对称的两个图形的对称线段_______，由此可得到，中心对称的两个图形是_____    _____.