

初中人教版24.1.1 圆导学案
展开
这是一份初中人教版24.1.1 圆导学案,共4页。学案主要包含了教学目标及重难点,学习过程,随堂检测等内容,欢迎下载使用。
24.1.3 弧、弦、圆心角 一、教学目标及重难点1、学习目标:(1)、理解圆心角的概念和圆的旋转不变性.(2)、利用圆的旋转不变性,探究并得出弧、弦、圆心角的关系,并能正确推理论证。(3)、通过观察、比较、推理、归纳等活动,发展推理能力以及概括问题的能力。2.学习重、难点:重点:探索关系定理并利用其解决相关问题.难点:定理中条件的理解及定理的探索.二、学习过程:1、思考:① 剪一个圆形纸片,把它绕圆心旋转180°和任意角度,观察旋转前后的两个图形是否重合,并填空:圆是 对称图形, 是它的对称中心;把圆绕着圆心旋转任意一个角度,旋转之后的图形都与原图形重合.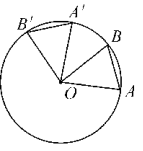 ② 的角叫做圆心角.2、探究:如图,∠AOB=∠A′OB′,那么,AB= A′B′, = 圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.几何语言:∵ ∠AOB=∠A′OB′,∴ AB= A′B′, = 结论1:在在同圆或等圆中,两个圆心角、两条弧、两条弦中如果有一组量相等,则它们所对应的其余各组量都 .结论2:在在同圆或等圆中,两个圆心角、两条弧、两条弦、两条弦心距中如果有一组量相等,则它们所对应的其余各组量都 。(知一得 )
② 的角叫做圆心角.2、探究:如图,∠AOB=∠A′OB′,那么,AB= A′B′, = 圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.几何语言:∵ ∠AOB=∠A′OB′,∴ AB= A′B′, = 结论1:在在同圆或等圆中,两个圆心角、两条弧、两条弦中如果有一组量相等,则它们所对应的其余各组量都 .结论2:在在同圆或等圆中,两个圆心角、两条弧、两条弦、两条弦心距中如果有一组量相等,则它们所对应的其余各组量都 。(知一得 ) 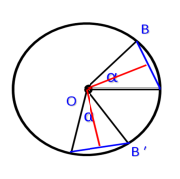 小结:在同圆或等圆中,如果
小结:在同圆或等圆中,如果 ![]() 两个圆心角, ②两条弧, ③两条弦, ④两条弦心距 中,有一组量相等,那么它们所对应的其余各组量都分别相等. 三、随堂检测(时间:12分钟满分:100分)1.(10分)如图,AB是⊙O的直径,
两个圆心角, ②两条弧, ③两条弦, ④两条弦心距 中,有一组量相等,那么它们所对应的其余各组量都分别相等. 三、随堂检测(时间:12分钟满分:100分)1.(10分)如图,AB是⊙O的直径,![]() ,∠AOE=72°,则∠COD的度数是( ) A.36° B.72° C.108° D.48°
,∠AOE=72°,则∠COD的度数是( ) A.36° B.72° C.108° D.48°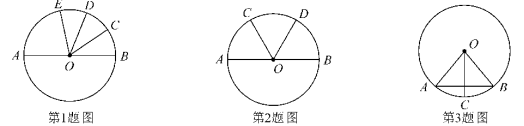 2.(15分)如图,已知AB是⊙O的直径,C、D是半圆上两个三等分点,则∠COD=
2.(15分)如图,已知AB是⊙O的直径,C、D是半圆上两个三等分点,则∠COD= ![]() 3.(15分)如图,在⊙O中,点C是的中点,∠A=50°,则∠BOC= 4. (15分) 如图,在⊙O中,AB=AC,∠C=75 , 求∠A的度数.
3.(15分)如图,在⊙O中,点C是的中点,∠A=50°,则∠BOC= 4. (15分) 如图,在⊙O中,AB=AC,∠C=75 , 求∠A的度数.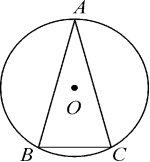 5. (15分)如图,在⊙O中,AD=BC,求证:AB=CD.
5. (15分)如图,在⊙O中,AD=BC,求证:AB=CD.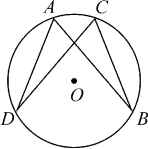 (二)、综合应用(20分)6.(20分) 如图,A、B是⊙O上的两点∠AOB=120°, C是AB的中点,求证:四边形OACB是菱形.
(二)、综合应用(20分)6.(20分) 如图,A、B是⊙O上的两点∠AOB=120°, C是AB的中点,求证:四边形OACB是菱形.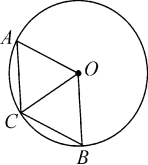 三、拓展延伸(10分)7.(10分)如图,在⊙O中,弦AB与CD相交于点E,AB=CD.(1)求证:△AEC≌△DEB;(2)点B与点C关于直线OE对称吗?试说明理由.
三、拓展延伸(10分)7.(10分)如图,在⊙O中,弦AB与CD相交于点E,AB=CD.(1)求证:△AEC≌△DEB;(2)点B与点C关于直线OE对称吗?试说明理由.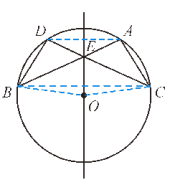
相关学案
这是一份初中数学人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.3 弧、弦、圆心角导学案及答案,共5页。学案主要包含了旧知回顾,新知梳理,试一试等内容,欢迎下载使用。
这是一份初中人教版24.1.3 弧、弦、圆心角学案,共4页。学案主要包含了课时安排,第二课时,学习目标,学习重难点,学习过程,达标检测,拓展创新等内容,欢迎下载使用。
这是一份初中人教版24.1.1 圆学案,共3页。学案主要包含了创设情境,探究新知,例题讲解,巩固练习,课堂小结等内容,欢迎下载使用。










