
2022-2023学年新疆乌鲁木齐六十八中七年级(下)期末数学试卷
展开2022-2023学年新疆乌鲁木齐六十八中七年级(下)期末数学试卷
一、选择题(共计24分)
1.(3分)若A,B,C是直线l上的三点,P是直线l外一点,PB=4cm,PC=3cm( )
A.等于3cm B.大于3cm而小于4cm
C.不大于3cm D.小于3cm
2.(3分)如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE B.∠A=∠EBD C.∠C=∠ABC D.∠A=∠ABE
3.(3分)下列调查中,最适宜采用普查方式的是( )
A.对我国初中学生视力状况的调查
B.对量子科学通信卫星上某种零部件的调查
C.对一批节能灯管使用寿命的调查
D.对“最强大脑”节目收视率的调查
4.(3分)在,0,,,,3.14,5.2020020002…(每两个2之间依次多一个0),无理数的个数是( )
A.1个 B.2个 C.3个 D.4个
5.(3分)一个数的两个平方根分别是2a﹣1与﹣a+2,则这个数是( )
A.﹣1 B.3 C.9 D.﹣3
6.(3分)已知点M(3a﹣2,a+6).若点M到两坐标轴的距离相等,则a的值为( )
A.4 B.﹣6 C.﹣1或4 D.﹣6或
7.(3分)如果a<b,那么下列不等式中,成立的是( )
A.a+5>b+5 B.﹣2a<﹣2b C.b﹣a<0 D.1﹣a>1﹣b
8.(3分)若整数a使关于x的不等式组至少有4个整数解,且关于x的方程(a+2),那么所有满足条件的整数a的个数是( )
A.8 B.5 C.4 D.3
二、填空题(共计18分)
9.(3分)在一次数学测试中,把某班40名学生的成绩分为六组,第一组到第四组的频数分别为4、6、7、10,则第六组的频数是 .
10.(3分)用不等式表示“x与1的和是负数”是 .
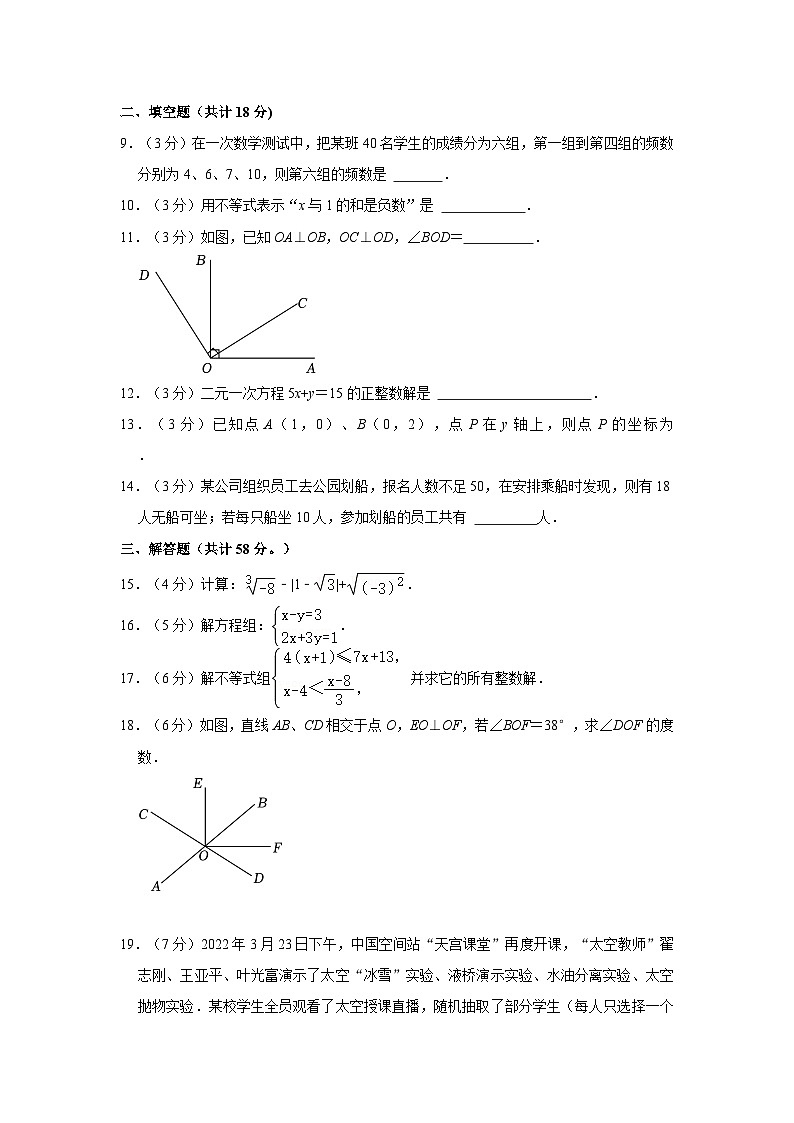
11.(3分)如图,已知OA⊥OB,OC⊥OD,∠BOD= .
12.(3分)二元一次方程5x+y=15的正整数解是 .
13.(3分)已知点A(1,0)、B(0,2),点P在y轴上,则点P的坐标为 .
14.(3分)某公司组织员工去公园划船,报名人数不足50,在安排乘船时发现,则有18人无船可坐;若每只船坐10人,参加划船的员工共有 人.
三、解答题(共计58分。)
15.(4分)计算:﹣|1﹣|+.
16.(5分)解方程组:.
17.(6分)解不等式组并求它的所有整数解.
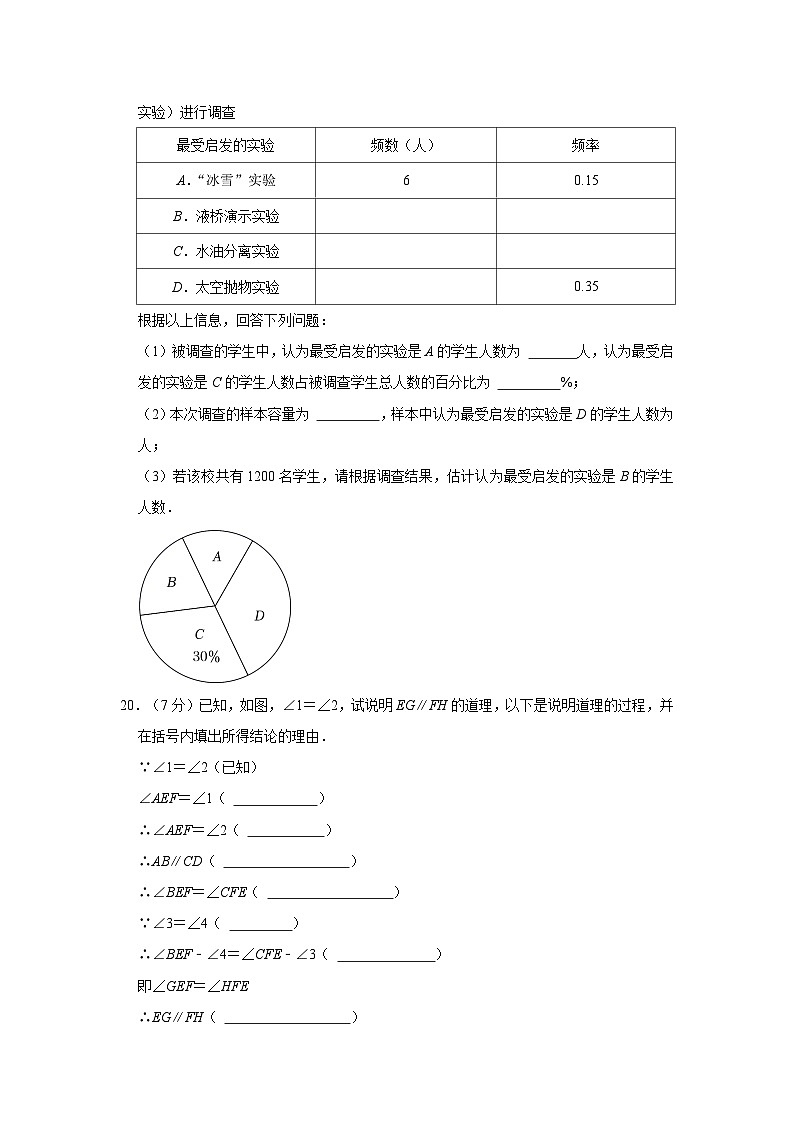
18.(6分)如图,直线AB、CD相交于点O,EO⊥OF,若∠BOF=38°,求∠DOF的度数.
19.(7分)2022年3月23日下午,中国空间站“天宫课堂”再度开课,“太空教师”翟志刚、王亚平、叶光富演示了太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验.某校学生全员观看了太空授课直播,随机抽取了部分学生(每人只选择一个实验)进行调查
最受启发的实验
频数(人)
频率
A.“冰雪”实验
6
0.15
B.液桥演示实验
C.水油分离实验
D.太空抛物实验
0.35
根据以上信息,回答下列问题:
(1)被调查的学生中,认为最受启发的实验是A的学生人数为 人,认为最受启发的实验是C的学生人数占被调查学生总人数的百分比为 %;
(2)本次调查的样本容量为 ,样本中认为最受启发的实验是D的学生人数为 人;
(3)若该校共有1200名学生,请根据调查结果,估计认为最受启发的实验是B的学生人数.
20.(7分)已知,如图,∠1=∠2,试说明EG∥FH的道理,以下是说明道理的过程,并在括号内填出所得结论的理由.
∵∠1=∠2(已知)
∠AEF=∠1( )
∴∠AEF=∠2( )
∴AB∥CD( )
∴∠BEF=∠CFE( )
∵∠3=∠4( )
∴∠BEF﹣∠4=∠CFE﹣∠3( )
即∠GEF=∠HFE
∴EG∥FH( )
21.(8分)“中国人的饭碗必须牢牢掌握在咱们自己手中”.为扩大粮食生产规模,某粮食生产基地计划投入一笔资金购进甲、乙两种农机具,已知购进2件甲种农机具和1件乙种农机具共需3.5万元
(1)求购进1件甲种农机具和1件乙种农机具各需多少万元?
(2)若该粮食生产基地计划购进甲、乙两种农机具共10件,且投入资金不少于9.8万元又不超过12万元,设购进甲种农机具m件,最少资金是多少?
22.(7分)三角形ABC与三角形A′B′C′在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A ;B ;C ;
(2)三角形ABC由三角形A′B′C′经过怎样的平移得到?答: .
(3)若点P(x,y)是三角形ABC内部一点,则它在三角形A′B′C′内部的对应点P′的坐标为 ;
(4)三角形ABC的面积等于 .
23.(8分)如图,AB∥CD,定点E,CD上,平行线AB,Q.
(1)如图1,当点P在EF的左侧时,∠AEP,∠PFC满足数量关系为 ;如图2,当点P在EF的右侧时,∠AEP,∠PFC满足数量关系为 ;
(2)如图3,若点P,Q都在EF的左侧,FP分别平分∠AEQ,∠CFQ .
(3)如图4,若点P在EF的左侧,点Q在EF的右侧且EP,∠CFQ,则∠EPF和∠EQF有怎样的数量关系?请说明理由.
2022-2023学年新疆乌鲁木齐六十八中七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本题共计8小题,每题3分,共计24分)
1.(3分)若A,B,C是直线l上的三点,P是直线l外一点,PB=4cm,PC=3cm( )
A.等于3cm B.大于3cm而小于4cm
C.不大于3cm D.小于3cm
【答案】C
【分析】根据“从直线外一点到这条直线上各点所连的线段中,垂线段最短”可知垂线段的长度不能超过PC的长.
【解答】解:根据点到直线的距离的定义,点P到直线L的距离即为点P到直线L的垂线段的长度.故选:C.
2.(3分)如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE B.∠A=∠EBD C.∠C=∠ABC D.∠A=∠ABE
【答案】D
【分析】在复杂的图形中具有相等关系的两角,首先要判断它们是否是同位角或内错角,被判断平行的两直线是否由“三线八角”而产生的被截直线.
【解答】解:A、∠C=∠ABE不能判断出EB∥AC;
B、∠A=∠EBD不能判断出EB∥AC;
C、∠C=∠ABC只能判断出AB=AC,故C选项不符合题意;
D、∠A=∠ABE,两直线平行,故D选项符合题意.
故选:D.
3.(3分)下列调查中,最适宜采用普查方式的是( )
A.对我国初中学生视力状况的调查
B.对量子科学通信卫星上某种零部件的调查
C.对一批节能灯管使用寿命的调查
D.对“最强大脑”节目收视率的调查
【答案】B
【分析】调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来,具体问题具体分析,普查结果准确,所以在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.
【解答】解:A、对我国初中学生视力状况的调查,调查的工作量大,故此选项错误;
B、对量子科学通信卫星上某种零部件的调查,必须全面调查;
C、对一批节能灯管使用寿命的调查具有破坏性,故此选项错误;
D、对“最强大脑”节目收视率的调查,不便测量,故本选项错误;
故选:B.
4.(3分)在,0,,,,3.14,5.2020020002…(每两个2之间依次多一个0),无理数的个数是( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】根据无理数的定义进行判断即可.
【解答】解:,,8.2020020002…(每两个2之间依次多一个0)是无理数,故C正确.
故选:C.
5.(3分)一个数的两个平方根分别是2a﹣1与﹣a+2,则这个数是( )
A.﹣1 B.3 C.9 D.﹣3
【答案】C
【分析】根据一个数的两个平方根的特点,列方程求出a的值,进而确定这个数.
【解答】解:由题意得,
2a﹣1﹣a+2=0,
解得a=﹣1,
所以6a﹣1=﹣3,﹣a+6=3,
即一个数的两个平方根分别是3与﹣4,
所以这个数是9,
故选:C.
6.(3分)已知点M(3a﹣2,a+6).若点M到两坐标轴的距离相等,则a的值为( )
A.4 B.﹣6 C.﹣1或4 D.﹣6或
【答案】C
【分析】根据点到两坐标轴的距离相等列出绝对值方程,然后求解即可.
【解答】解:∵点M(3a﹣2,a+6)到两坐标轴的距离相等,
∴|3a﹣2|=|a+8|,
∴3a﹣2=a+7或3a﹣2=﹣(a+4),
解得a=4或a=﹣1.
故选:C.
7.(3分)如果a<b,那么下列不等式中,成立的是( )
A.a+5>b+5 B.﹣2a<﹣2b C.b﹣a<0 D.1﹣a>1﹣b
【答案】D
【分析】根据不等式的性质:不等式两边加(或减)同一个数(或式子),不等号的方向不变;不等式两边乘(或除以)同一个正数,不等号的方向不变;不等式两边乘(或除以)同一个负数,不等号的方向改变.可得答案.
【解答】解:A、不等式a<b两边都加上5可得a+5<b+3;
B、不等式a<b两边都乘以﹣2可得﹣2a>﹣7b;
C、不等式a<b两边都减去b可得a﹣b<0,故本选项不合题意;
D、不等式a<b两边都都乘以﹣1可得﹣a>﹣b,故本选项符合题意.
故选:D.
8.(3分)若整数a使关于x的不等式组至少有4个整数解,且关于x的方程(a+2),那么所有满足条件的整数a的个数是( )
A.8 B.5 C.4 D.3
【答案】D
【分析】分别将不等式组的解集,方程的解表示出来,确定a的取值范围即可.
【解答】解:,
解不等式①得:x≤2,
解不等式②得:x>a+2,
∴不等式的解集为:a+6<x≤2,
∵至少有4个整数解,
∴a+5<﹣1,
∴a<﹣3,
(a+4)x=8,
解得:x=,
∵为整数,
∴a+5=±1或a+2=±7或a+2=±4或a+2=±8,
∵∴a<﹣3,
∴a=﹣2或﹣6或﹣10,
∴满足条件的a的个数为3个.
故选:D.
二、填空题(本题共计6小题,每题3分,共计18分
9.(3分)在一次数学测试中,把某班40名学生的成绩分为六组,第一组到第四组的频数分别为4、6、7、10,则第六组的频数是 5 .
【答案】见试题解答内容
【分析】首先求出第五组的频数,进而得出第六组的频数.
【解答】解:∵某班40名学生的成绩分为六组,第五组频率是0.2,
∴第五组的频数是:40×4.2=8,
∵第一组到第四组的频数分别为6、6、7、10,
∴第六组频数是:40﹣2﹣6﹣7﹣10﹣6=5.
故答案为:5.
10.(3分)用不等式表示“x与1的和是负数”是 x+1<0 .
【答案】x+1<0.
【分析】先表示出“x与1的和”,然后确定不等号,列出不等式即可.
【解答】解:由题意得:x+1<0,
故答案为:x+2<0.
11.(3分)如图,已知OA⊥OB,OC⊥OD,∠BOD= 32° .
【答案】32°.
【分析】根据同角的余角相等解答.
【解答】解:∵OA⊥OB,
∴∠AOC与∠BOC互为余角,
∵OC⊥OD,
∴∠BOD与∠BOC互为余角,
∴根据同角的余角相等,得∠AOC=∠BOD=32°,
故答案为:32°.
12.(3分)二元一次方程5x+y=15的正整数解是 , .
【答案】见试题解答内容
【分析】先确定x的取值范围,再用试验的办法得到方程的正整数解.
【解答】解:∵y>0,即15﹣3x>2,
解得x<5.
由题意得y=15﹣5x
当x=2时,y=10;
当x=2时,y=5;
当x=2时,y=0(不合题意);
当x=4时,y=﹣6(不合题意);
当x=5时,y﹣=﹣10(不合题意).
故答案为:,.
13.(3分)已知点A(1,0)、B(0,2),点P在y轴上,则点P的坐标为 (0,12)或(0,﹣8) .
【答案】见试题解答内容
【分析】根据A点的坐标可知BP边上的高为1,而△PAB的面积为5,点P在y轴上,说明BP=10,已知点B的坐标,可求P点坐标.
【解答】解:∵A(1,0),8),
∴BP边上的高为1,
又△PAB的面积为5,
∴BP=10,
而点P可能在点B(6,2)的上边或者下边,
∴P(0,12)或(3.
故答案为:(0,12)或(0
14.(3分)某公司组织员工去公园划船,报名人数不足50,在安排乘船时发现,则有18人无船可坐;若每只船坐10人,参加划船的员工共有 48 人.
【答案】48.
【分析】假设共安排x艘船,根据报名人数不足50人,在安排乘船时发现,每只船坐6人,就剩下18人无船可乘,则可知划船员工数是6x+18且6x+18<50;若每只船坐10人,那么其余的船坐满后有一只船不空也不满,则10(x﹣1)+1≤6x+18<10x,解得x代入6x+18即是划船的员工数.
【解答】解:设共安排x艘船,
根据题意得:,
解不等式①,得:,
解不等式②,得:,
∴不等式组的解集为:,
∴x=8,
∴划船员工数为:6x+18=48(人),
∴参加划船的员工共有48人.
故答案为:48.
三、解答题(本题共计9小题,共计58分。)
15.(4分)计算:﹣|1﹣|+.
【答案】2﹣.
【分析】先化简各式,然后再进行计算即可解答.
【解答】解:﹣|2﹣
=﹣2﹣(﹣6)+3
=﹣2﹣+1+3
=2﹣.
16.(5分)解方程组:.
【答案】.
【分析】先用加减消元法求出x的值,再代入①求出y的值即可.
【解答】解:,
①×3+②得,4x=10,
解得x=2,
把x=2代入①得,8﹣y=3,
解得y=﹣1,
故方程组的解为.
17.(6分)解不等式组并求它的所有整数解.
【答案】﹣3≤x<2,整数解为:﹣3,﹣2,﹣1,0,1.
【分析】先求出不等式组的解集,再求出不等式组的整数解即可.
【解答】解:,
由①得,x≥﹣3,
由②得,x<2,
所以,不等式组的解集是﹣2≤x<2,
所以,它的整数解为:﹣3,﹣5,0,1.
18.(6分)如图,直线AB、CD相交于点O,EO⊥OF,若∠BOF=38°,求∠DOF的度数.
【答案】∠DOF的度数为26°.
【分析】先根据垂直定义可得∠EOF=90°,从而可得∠EOB=52°,然后利用平角定义可得∠AOE=128°,再利用角平分线的定义可得∠COE=64°,最后利用平角定义进行计算,即可解答.
【解答】解:∵EO⊥OF,
∴∠EOF=90°,
∵∠BOF=38°,
∴∠EOB=∠EOF﹣∠BOF=52°,
∴∠AOE=180°﹣∠BOE=128°,
∵OC平分∠AOE,
∴∠COE=∠AOE=64°,
∴∠DOF=180°﹣∠COE﹣∠EOF=26°,
∴∠DOF的度数为26°.
卷Ⅱ(非选择题
19.(7分)2022年3月23日下午,中国空间站“天宫课堂”再度开课,“太空教师”翟志刚、王亚平、叶光富演示了太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验.某校学生全员观看了太空授课直播,随机抽取了部分学生(每人只选择一个实验)进行调查
最受启发的实验
频数(人)
频率
A.“冰雪”实验
6
0.15
B.液桥演示实验
C.水油分离实验
D.太空抛物实验
0.35
根据以上信息,回答下列问题:
(1)被调查的学生中,认为最受启发的实验是A的学生人数为 6 人,认为最受启发的实验是C的学生人数占被调查学生总人数的百分比为 30 %;
(2)本次调查的样本容量为 40 ,样本中认为最受启发的实验是D的学生人数为 14 人;
(3)若该校共有1200名学生,请根据调查结果,估计认为最受启发的实验是B的学生人数.
【答案】(1)6;30;
(2)40;14;
(3)240人.
【分析】(1)由频数分布表可得认为最受启发的实验是A的学生人数,由扇形图可得认为最受启发的实验是C的学生人数占被调查学生总人数的百分比;
(2)由A组的学生人数及其频率可得本次调查的样本容量,用总人数乘频率可得样本中认为最受启发的实验是D的学生人数;
(3)用样本估计总体即可.
【解答】解:由题意可知,被调查的学生中,认为最受启发的实验是C的学生人数占被调查学生总人数的百分比为30%,
故答案为:6;30;
(2)本次调查的样本容量为:6÷8.15=40;
样本中认为最受启发的实验是D的学生人数为:40×0.35=14(人),
故答案为:40;14;
(3)样本中认为最受启发的实验是B的学生人数为:40﹣6﹣14﹣40×30%=7(人),
1200×=240(人),
答:估计该校认为最受启发的实验是B的学生人数为240人.
20.(7分)已知,如图,∠1=∠2,试说明EG∥FH的道理,以下是说明道理的过程,并在括号内填出所得结论的理由.
∵∠1=∠2(已知)
∠AEF=∠1( 对顶角相等 )
∴∠AEF=∠2( 等量代换 )
∴AB∥CD( 同位角相等,两直线平行 )
∴∠BEF=∠CFE( 两直线平行,内错角相等 )
∵∠3=∠4( 已知 )
∴∠BEF﹣∠4=∠CFE﹣∠3( 等式的基本性质 )
即∠GEF=∠HFE
∴EG∥FH( 内错角相等,两直线平行 )
【答案】对顶角相等;等量代换;同位角相等,两直线平行;两直线平行,内错角相等;已知;等式的基本性质;内错角相等,两直线平行.
【分析】利用对顶角相等得出∠AEF=∠1,再利用平行线的判定定理和性质定理可得∠BEF=∠CEF,易得∠GEF=∠HFE,利用内错角相等,两直线平行可得结论.
【解答】解:∵∠1=∠2(已知),
∠AEF=∠7 (对顶角相等),
∴∠AEF=∠2 (等量代换),
∴AB∥CD (同位角相等,两直线平行),
∴∠BEF=∠CEF (两直线平行,内错角相等),
∵∠3=∠2(已知)
∴∠BEF﹣∠4=∠CEF﹣∠3 (等式的基本性质),
即∴∠GEF=∠HFE
∴EG∥FH (内错角相等,两直线平行).
故答案为:对顶角相等;等量代换,两直线平行,内错角相等;等式的基本性质,两直线平行.
21.(8分)“中国人的饭碗必须牢牢掌握在咱们自己手中”.为扩大粮食生产规模,某粮食生产基地计划投入一笔资金购进甲、乙两种农机具,已知购进2件甲种农机具和1件乙种农机具共需3.5万元
(1)求购进1件甲种农机具和1件乙种农机具各需多少万元?
(2)若该粮食生产基地计划购进甲、乙两种农机具共10件,且投入资金不少于9.8万元又不超过12万元,设购进甲种农机具m件,最少资金是多少?
【答案】(1)购进1件甲种农机具1.5万元,购进1件乙种农机具0.5万元;
(2)有3种购买方案如下:
方案一:购进甲种农机具5件,乙种农机具5件,总资金为10万元,
方案二:购进甲种农机具6件,乙种农机具4件,总资金为11万元,
方案三:购进甲种农机具7件,乙种农机具3件,总资金为12万元,
购进甲种农机具5件,乙种农机具5件,总资金最少,最少资金为10万元.
【分析】(1)设购进1件甲种农机具x万元,购进1件乙种农机具y万元,根据购进2件甲种农机具和1件乙种农机具共需3.5万元,购进1件甲种农机具和3件乙种农机具共需3万元,列二元一次方程组,求解即可;
(2)根据投入资金不少于9.8万元又不超过12万元,列一元一次不等式组,求出m的取值范围,取正整数,即可确定有哪几种购买方案,并求出哪种方案资金最少以及最少资金.
【解答】解:(1)设购进1件甲种农机具x万元,购进1件乙种农机具y万元,
根据题意,得,
解得,
答:购进4件甲种农机具1.5万元,购进2件乙种农机具0.5万元;
(2)根据题意,得,
解得4.8≤m≤4,
∵m是正整数,
∴m可取5,6,6,
有3种购买方案如下:
方案一:购进甲种农机具5件,乙种农机具7件,
方案二:购进甲种农机具6件,乙种农机具4件,
方案三:购进甲种农机具8件,乙种农机具3件,
∵10<11<12,
∴购进甲种农机具5件,乙种农机具2件,最少资金为10万元.
22.(7分)三角形ABC与三角形A′B′C′在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A (1,3) ;B (2,0) ;C (3,1) ;
(2)三角形ABC由三角形A′B′C′经过怎样的平移得到?答: 将△A′B′C′向右平移4个单位长度,再向上平移2个单位长度即可得到△ABC .
(3)若点P(x,y)是三角形ABC内部一点,则它在三角形A′B′C′内部的对应点P′的坐标为 (x﹣4,y﹣2) ;
(4)三角形ABC的面积等于 2 .
【答案】(1)(1,3),(2,0),(3,1);
(2)将△ABC向左平移4个单位长度,再向下平移2个单位长度即可得到△A′B′C′;
(3)(x﹣4,y﹣2);
(4)2.
【分析】(1)根据题图写出A、B、C的坐标即可;
(2)将△A′B′C′向右平移4个单位长度,再向上平移2个单位长度即可得到△A′B′C′;
(3)根据(2)的平移过程即可得P′坐标;
(4)用A、B、C点所在的矩形的面积减去规则的小三角形的面积即可得△ABC的面积;
【解答】解:(1)根据题图可得:A(1,3),8),1).
故答案为:(1,5),0),1);
(2)将△A′B′C′向右平移2个单位长度,再向上平移2个单位长度即可得到△ABC.
故答案为:将△A′B′C′向右平移4个单位长度,再向上平移7个单位长度即可得到△ABC;
(3)根据平移的性质,P′(x﹣4.
故答案为:(x﹣4,y﹣8);
(4)S△ABC=3×2﹣(×1×5+×1×2)=2.
故答案为:2.
23.(8分)如图,AB∥CD,定点E,CD上,平行线AB,Q.
(1)如图1,当点P在EF的左侧时,∠AEP,∠PFC满足数量关系为 ∠AEP+∠PFC=∠EPF ;如图2,当点P在EF的右侧时,∠AEP,∠PFC满足数量关系为 ∠AEP+∠EPF+∠PFC=360° ;
(2)如图3,若点P,Q都在EF的左侧,FP分别平分∠AEQ,∠CFQ ∠EQF=2∠EPD .
(3)如图4,若点P在EF的左侧,点Q在EF的右侧且EP,∠CFQ,则∠EPF和∠EQF有怎样的数量关系?请说明理由.
【答案】(1)∠AEP+∠PFC=∠EPF,∠AEP+∠EPF+∠PFC=360°;
(2)∠EQF=2∠EPD;
(3)∠EQF+2∠EPD=360°.
【分析】(1)过点P作PH∥AB,根据平行线的性质得AB∥PH∥CD,进而得∠AEP=∠EPH,∠PFC=∠HPF,据此即可得出结论;当点P在EF的右侧时,由上述结论得∠EPF=∠BEP+∠DFP,再根据平角的定义得∠BEP=180°﹣∠AEP,∠DFP=180°﹣∠PFC,据此即可得出结论;
(2)先由角平分线的定义得∠AEQ=2∠AEP,∠CFQ=2∠CFP,再由(1)的结论得∠EPD=∠AEP+∠CFP,∠EQF=∠AEQ+∠CFQ,据此即可得出结论;
(3)先由角平分线的定义得∠AEQ=2∠AEP,∠CFQ=2∠CFP,再由(1)的结论得∠EPF=∠AEP+∠CFP,∠EQF+∠AEQ+∠CFQ=360°,据此即可得出结论.
【解答】解:(1)当点P在EF的左侧时,满足∠AEP+∠PFC=∠EPF.
理由如下:
过点P作PH∥AB,如图所示:
∵AB∥CD,
∴AB∥PH∥CD,
∴∠AEP=∠EPH,∠PFC=∠HPF,
∴∠AEP+∠PFC=∠EPH+∠HPF,
即:∠AEP+∠PFC=∠EPF;
当点P在EF的右侧时,满足∠AEP+∠EPF+∠PFC=360°.
理由如下:
由上述结论得:∠EPF=∠BEP+∠DFP,
由平角的定义得:∠BEP=180°﹣∠AEP,∠DFP=180°﹣∠PFC,
∴∠EPF=180°﹣∠AEP+180°﹣∠PFC,
∴∠AEP+∠EPF+∠PFC=360°;
故答案为:∠AEP+∠PFC=∠EPF,∠AEP+∠EPF+∠PFC=360°.
(2)∠EQF=2∠EPD,理由如下:
∵EP,FP分别平分∠AEQ,
∴∠AEQ=2∠AEP,∠CFQ=2∠CFP,
由(1)的结论得:∠EPD=∠AEP+∠CFP,∠EQF=∠AEQ+∠CFQ,
∴∠EQF=∠AEQ+∠CFQ=2(∠AEP+∠CFP)=2∠EPD,
∴∠EPF和∠EQF的数量关系为:∠EQF=2∠EPD;
故答案为:∠EQF=2∠EPD.
(3)∠EQF+2∠EPF=360°,理由如下:
∵EP,FP分别平分∠AEQ,
∴∠AEQ=6∠AEP,∠CFQ=2∠CFP,
由(1)的结论得:∠EPF=∠AEP+∠CFP,∠EQF+∠AEQ+∠CFQ=360°,
∴∠EQF+2∠AEP+8∠CFP=360°,
∴∠EQF+2(∠AEP+∠CFP)=360°,
即:∠EQF+2∠EPF=360°.
2023-2024学年新疆乌鲁木齐八中七年级(上)期末数学试卷(含解析): 这是一份2023-2024学年新疆乌鲁木齐八中七年级(上)期末数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年新疆乌鲁木齐八中七年级(下)开学数学试卷(含解析): 这是一份2022-2023学年新疆乌鲁木齐八中七年级(下)开学数学试卷(含解析),共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
新疆乌鲁木齐市第六十八中学2022-2023学年下学期七年级期末数学试卷(含答案): 这是一份新疆乌鲁木齐市第六十八中学2022-2023学年下学期七年级期末数学试卷(含答案),共21页。试卷主要包含了选择题,填空题(共计18分),解答题等内容,欢迎下载使用。












