辽宁省丹东六中协作校联考2022-2023学年七年级下学期期末数学试卷（含答案）

这是一份辽宁省丹东六中协作校联考2022-2023学年七年级下学期期末数学试卷（含答案），共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年辽宁省丹东六中协作校联考七年级（下）期末数学试卷
学校:___________姓名：___________班级：___________考号：___________
第I卷（选择题）
一、选择题（本大题共10小题，共20.0分。在每小题列出的选项中，选出符合题目的一项）
1. 在中国园林建筑中，洞窗是最生动的眼睛，主要以漏空图案填心为主，故也称镂空花窗.花窗图案丰富多样，以各种植物，动物，字体，几何图案和其他图案为基础，相互交错形成多种吉祥图案.则下列填心的图案中不是轴对称图形的是(    )
A. B. C. D.
2. 在2021年发布的国际学术杂志《Nature》上了解到，当前垂直型晶体管已经可以使芯片工艺级别达到0.00000000065m，数据0.00000000065用科学记数法可表示为(    )
A. 65×l0-9 B. 6.5×10-10 C. 6.5×l0-11 D. 0.65×10-9
3. 一个三角形的两边长分别为3cm和5cm，则第三边的长可能是(    )
A. 1cm B. 2cm C. 7cm D. 8cm
4. 下列计算正确的是(    )
A. a4+a4=a8 B. a4⋅a4=a16 C. (a4)4=a16 D. a8÷a4=a2
5. 下列说法中正确的是(    )
A. 天宫六号货运飞船发射前各零件的检查是抽样调查
B. 某小组有13名同学，至少有2名同学的生日在同一个月
C. 可能性是1%的事件在一次试验中一定不会发生
D. 为了解近十年宿迁初中生的视力变化趋势，采用扇形统计图最合适
6. 若△ABC中，∠A：∠B：∠C=5：3：2，则△ABC是(    )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 任意三角形
7. 已知直线a/​/b，将一块含60°角的直角三角板ABC按如图所示方式放置，直角顶点A在直线a上，斜边BC与直线b相交.若∠1=72°，则∠2的度数为(    )
A. 32°
B. 40°
C. 42°
D. 45°
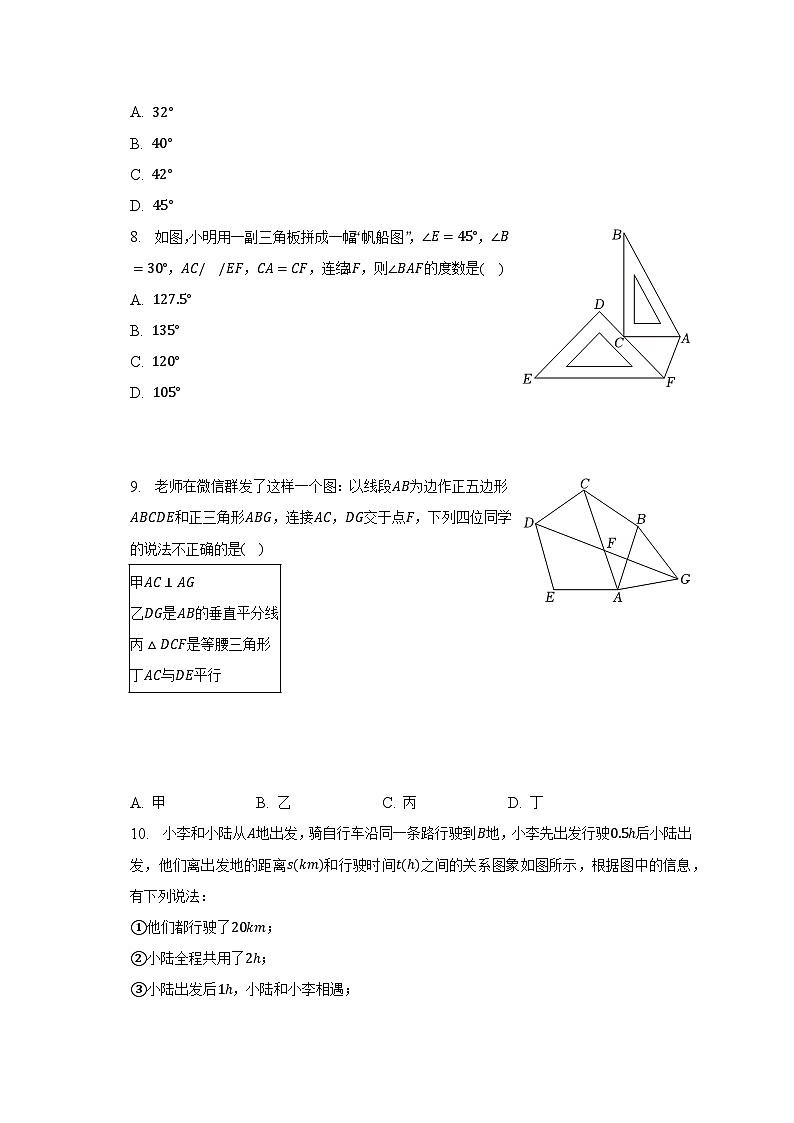
8. 如图，小明用一副三角板拼成一幅“帆船图”，∠E=45°，∠B=30°，AC/​/EF，CA=CF，连结AF，则∠BAF的度数是(    )
A. 127.5°
B. 135°
C. 120°
D. 105°


9. 老师在微信群发了这样一个图：以线段AB为边作正五边形ABCDE和正三角形ABG，连接AC，DG交于点F，下列四位同学的说法不正确的是(    )
甲AC⊥AG
乙DG是AB的垂直平分线
丙△DCF是等腰三角形
丁AC与DE平行



A. 甲 B. 乙 C. 丙 D. 丁
10. 小李和小陆从A地出发，骑自行车沿同一条路行驶到B地，小李先出发行驶0.5h后小陆出发，他们离出发地的距离s(km)和行驶时间t(h)之间的关系图象如图所示，根据图中的信息，有下列说法：
①他们都行驶了20km；
②小陆全程共用了2h；
③小陆出发后1h，小陆和小李相遇；
④小李在途中停留了0.5h；
其中正确的有(    )

A. 1个 B. 2个 C. 3个 D. 4个
第II卷（非选择题）
二、填空题（本大题共8小题，共24.0分）
11. 如图，直线AB、CD相交于点O，OE平分∠AOD，若∠BOC=80°，则∠COE的度数是______ ．


12. 现有三张正面印有2023年杭州亚运会吉祥物琮琮、宸宸和莲莲的不透明卡片，卡片除正面图案不同外，其余均相同.将三张卡片正面向下洗匀，从中随机抽取一张卡片，则抽出的卡片图案是琮琮的概率是______ ．

13. 学校七年级开展种植班树活动.已知一班的班树现在高80厘米，以后一年中每个月平均长高2厘米，x月后这棵树的高度为h厘米，则h与x的函数关系式为      ．
14. 已知y2-my+1是完全平方式，则m的值是______ ．
15. 如图，在△ABC中，AD⊥BC，AE平分∠BAC，若∠1=40°，∠2=25°，则∠B=______ ．


16. 小丽从一张等腰三角形纸片ABC(AB=AC)中恰好剪出五个如图所示的小等腰三角形，其中BC=BD，EC=EF=FG=DG=DA，则∠B=______°.


17. 如图，分别以a，b，m，n为边长作正方形，已知m>n且满足am-bn=2，an+bm=4．
(1)若a=3，b=4，则图1阴影部分的面积是______ ；
(2)若图1阴影部分的面积为3，图2四边形ABCD的面积为5，则图2阴影部分的面积是______ ．

18. 如图，在Rt△ABC中，AC=BC，点P是BC上一点，BD⊥AP交AP延长线于点D，连接CD，若图中两阴影三角形的面积之差为32(即，S△ACP-S△PBD=32 )，则CD=______ ．


三、解答题（本大题共8小题，共76.0分。解答应写出文字说明，证明过程或演算步骤）
19. (本小题16.0分)
计算：
(1)|-2|+(-1)2024×(π+3)0-(-13)-2；
(2)9992-1002×998+1 (简便运算)；
(3)(2xy2)3⋅y2÷(16x3y3)；
(4)(x+3y-2z)(x-3y+2z)．
20. (本小题8.0分)
先化简，再求值：[(2x+y)(2x-y)-(3x+y)(x-2y)-x2]÷(-12y)，其中x=-1，y=2．
21. (本小题7.0分)
在图示的正方形网格纸中，每个小正方形的边长都是1，△ABC的三个顶点都在小正方形的顶点处，直线MN与网格中竖直的线相重合．
(1)直接写出△ABC的面积；
(2)作出△ABC关于直线MN对称的△A'B'C'；
(3)在网格内找一点D，使点D到线段BC，B'C'的距离相等且DB=DC.(在网格上直接标出点D的位置，不写作法)

22. (本小题7.0分)
在一个不透明的盒子里装有除颜色外完全相同的红、白、黑三种颜色的球.其中红球3个，白球5个，黑球若干个，若从中任意摸出一个白球的概率是13．
(1)求盒子中黑球的个数；
(2)求任意摸出一个球是黑球的概率；
(3)能否通过只改变盒子中白球的数量，使得任意摸出一个球是红球的概率为14，若能，请写出如何调整白球数量；若不能，请说明理由．
23. (本小题8.0分)
已知∠1=∠2，∠3=∠4，∠5=∠A，试说明：BE/​/CF．
请完善下面解答过程，并填写理由．
解：∵∠3=∠4(已知)，
∴AE/​/      (      )，
∴∠EDC=      (两直线平行，内错角相等)，
∵∠5=∠A(已知)，
∴∠EDC=      (      )，
∴DC/​/AB(同位角相等，两直线平行)，
∴∠5+∠ABC=180°(      )，
即∠5+∠2+∠3=180°，
∵∠1=∠2(已知)，
∴∠5+∠1+∠3=180°(等量代换)，
即∠BCF+∠3=180°，
∴BE/​/      (      ).

24. (本小题10.0分)
如图，在△ABC中，D为AB上一点，E为AC中点，连接DE并延长至点F使得EF=ED，连CF．
(1)求证：CF/​/AB；
(2)连接BE，若∠ABE=25°，BE平分∠ABC，CA平分∠BCF，求∠A的度数．

25. (本小题8.0分)
甲、乙两车从A城出发匀速行驶至B城，在整个行驶过程中，甲、乙离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示，根据图象信息解答下列问题：
(1)甲车的速度是______ ；
(2)乙车用了______ 小时到达B城；
(3)求乙车出发后多少时间追上甲车？
(4)求甲车出发多少时间，两车相距50千米？

26. (本小题12.0分)
在△ABC和△DCE中，CA=CB，CD=CE，∠CAB=∠CED=α．

(1)如图1，将AD、EB延长，延长线相交于点O：
①求证：BE=AD；
②用含α的式子表示∠AOB的度数(直接写出结果)；
(2)如图2，当α=45°时，连接BD、AE，作CM⊥AE于M点，延长MC与BD交于点N，求证：N是BD的中点．
答案和解析

1.【答案】D 
【解析】解：A、是轴对称图形，不符合题意，
B、是轴对称图形，不符合题意，
C、是轴对称图形，不符合题意，
D、不是轴对称图形，符合题意，
故选：D．
根据轴对称图形的概念逐项判定即可．
本题考查了轴对称图形的定义，正确理解定义是解题的关键．

2.【答案】B 
【解析】解：0.00000000065=6.5×10-10．
故选：B．
科学记数法的表示形式为a×10n的形式，其中1≤|a|