小学5 圆3 圆的面积课前预习ppt课件

第6 课时 有关“外方内圆”和“外圆内方”的

组合图形的面积问题 （教案）

教学内容  教材第67 页例3。

教学目标  1. 结合具体的情境，利用圆的面积计算公式解决有关“外方内圆”和“外圆内方”的实际问题。

2. 提高分析问题和解决问题的能力。

3. 结合例题渗透传统文化的教育，使学生将数学和实际生活联系起来，感受数学的价值，提升学习的兴趣。

教学重点 会解决有关“外方内圆”和“外圆内方”的实际问题。

教学难点 理解图形中正方形和圆的关系。

教学方法 观察、推理、验证。

教学准备 多媒体课件。

教学过程

一、新课导入

1. 出示课件。

师：仔细观察这两幅图，你发现了什么？

预设1：左边的雕窗外面是方的里面是圆的，右边的雕窗外面是圆的里面 是方的。

预设2 ：都是由圆和正方形这两种图形组成的。

2. 揭示课题。

师： 中国建筑非常讲究传统文化美。这两幅图就是中国建筑中常见的“外 方内圆”和“外圆内方”的设计，在生活中都能经常见到。今天我们就来利用已有的知识解决有关“外方内圆”和“外圆内方”的组合图形的面积问题。（板书课题）

设计意图 通过展示中国建筑中经常能见到的“外方内圆”和“外圆内方”  设计，为学习本课内容作好了铺垫。

二、探究新知

探究点  解决“外方内圆”和“外圆内方”的组合图形的面积问题

1. 阅读与理解。

下图中的两个圆半径都是1 m，你能求出正方形和圆之间部分的面积吗？

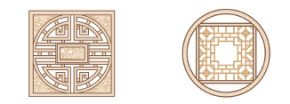
师：从题中你得到了哪些信息？

预设1 ：知道了两个圆的半径都是1 m。

预设2 ：左图求的是正方形比圆多的面积，右图求的是圆比正方形多的面积。

2. 分析与解答。

把实物图用下面的图（1）、图（2）来表示。

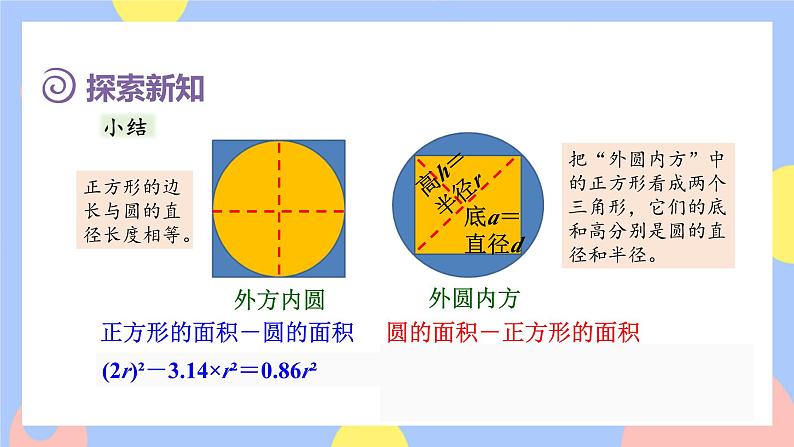
（1）观察图（1）。

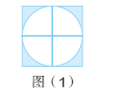
师：正方形和圆有什么关系？

预设：正方形的边长= 圆的直径。

师：“外方内圆”中正方形的边长与圆的直径长度相等。

师：如何求阴影部分的面积？

预设：阴影部分的面积= 正方形的面积- 圆的面积。

师：如何计算图（1）中阴影部分的面积？（根据学生回答适当板书）

预设 ：正方形的边长：1×2=2（m）

正方形的面积：2×2=4（）

圆的面积：3.14×=3.14（）

阴影部分的面积：4-3.14=0.86（）

答：阴影部分的面积是0.86。

（2）观察图（2）。

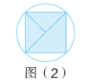
师：“外圆内方”中正方形的边长是多少呢？

预设 ：可以把“外圆内方”中的正方形看成两个三角形，它们的底和高分  别是圆的直径和半径。

师：如何计算图（2）阴影部分的面积？（根据学生回答适当板书）

预设：阴影部分的面积= 圆的面积- 两个三角形的面积和。

圆的面积：3.14×=3.14（）

两个三角形的面积和：×（1×2）×1×2=2（）

阴影部分的面积：3.14-2=1.14（）

答：阴影部分的面积是1.14。

3. 回顾与反思。

师：如果两个圆的半径都是r，结果又是怎样的？

预设1 ：图（1）：-3.14 2=0.86 。

预设2 ：图（2）：3.14 -×2r×r ×2=1.14 。

师：当r=1 m 时，结果有什么变化吗？

预设：没变化，和前面的结果完全一致。

4. 小结 ：“外方内圆”中正方形的边长与圆的直径长度相等，阴影部分的 面积= 正方形的面积- 圆的面积。“外圆内方” 中正方形是由2 个底是2 cm，高是1 cm的三角形组成的，底是圆的直径，高是圆的半径，阴影部分的面积= 圆的面积- 两个三角形的面积和。

设计意图 通过课件展示中国建筑中经常能见到的“外方内圆”和“外圆内 方”设计，学生可以形象直观地感受“外方内圆”和“外圆内方”的特征，根据特征，找出解决问题的方法，培养了学生分析问题和解决问题的能力。

三、当堂练习

1. 课件出示的题目。

2. 出示教材“做一做”的题目。

设计意图 通过不同形式的练习，学生能运用“外方内圆”和“外圆内方”   的特征解决问题。

四、课堂总结

师：这节课你有什么收获？（学生交流，教师总结出示）

1.“外方内圆”图形中，圆的直径等于正方形的边长。如果圆的半径为r，那么正方形和圆之间部分的面积为0.86 。

2. “外圆内方” 图形中，这个正方形的对角线等于圆的直径。如果圆的半径为r，那么正方形和圆之间部分的面积为1.14 。

五、课后作业

请完成教材练习十五第9 题。

六、板书设计

七、教学反思

成功之处 本节课由传统文化对建筑设计产生的影响导入新课，自然地引出例题教学，极大地激发了学生学习的兴趣和探索的热情。让学生经历观察思考、分析推理等学习活动，得到公共边以及图形各要素之间的关系，自主地运用已有的知识解决问题。在层层深入的学习过程中，教师始终坚持为学生创设探索的情境，利用知识内在的魅力吸引学生主动投入到知识的探索过程中。

不足之处 在让学生求面积的时候没有放手让学生自己完成，今后还需要把课堂更多地交给学生，以学生为主体。