2022-2023学年陕西省宝鸡市教育联盟高二（下）联考数学试卷（文科）（7月份）（含解析）

这是一份2022-2023学年陕西省宝鸡市教育联盟高二（下）联考数学试卷（文科）（7月份）（含解析），共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年陕西省宝鸡市教育联盟高二（下）联考数学试卷（文科）（7月份）
一、单选题（本大题共12小题，共60.0分。在每小题列出的选项中，选出符合题目的一项）
1. |21−i|=(    )
A. 22 B. 1 C. 2 D. 2
2. 参数方程为x=t+1y=t2+2t(t为参数)的曲线必过点(    )
A. (1,2) B. (−2,1) C. (2,3) D. (0,1)
3. 如图，把空间中直线与平面的位置关系：①直线在平面内；②直线不在平面内；③直线与平面相交；④直线与平面平行，依次填入结构图中的E，F，G，H中，则正确的填写顺序是(    )

A. ①③②④ B. ②①③④ C. ③②①④ D. ①④③②
4. 用反证法证明命题时，对结论：“自然数a，b，c中至少有一个是奇数”正确的假设为(    )
A. a，b，c都是偶数 B. a，b，c都是奇数
C. a，b，c中至少有两个奇数 D. a，b，c中至少有两个偶数或都是奇数
5. 新能源汽车的核心部件是动力电池，电池成本占了新能源整车成本很大的比例，而其中的原材料碳酸锂又是电池的主要成分．从2020年底开始，碳酸锂的价格一路水涨船高，下表是2021年我国江西某企业的前5个月碳酸锂价格与月份的统计数据：
月份代码x
1
2
3
4
5
碳酸锂价格y(万元/kg)
0.5
0.6
1
1.4
1.5
由上表可知其线性回归方程为y =0.28x+a ，则a =(    )
A. 0.16 B. 0.18 C. 0.30 D. 0.32
6. 在极坐标系中，与圆ρ=4sinθ相切的一条直线的方程为(    )
A. ρcosθ=2 B. ρsinθ=2 C. ρsin(θ+π3)=4 D. ρsin(θ−π3)=4
7. 设P= 2，Q= 7− 3，R= 6− 2，则P，Q，R的大小顺序是(    )
A. P>Q>R B. P>R>Q C. Q>P>R D. Q>R>P
8. 德国数学家莱布尼兹(1646年−1716年)于1674年得到了第一个关于π的级数展开式，该公式于明朝初年传入我国．在我国科技水平业已落后的情况下，我国数学家、天文学家明安图(1692年−1765年)为提高我国的数学研究水平，从乾隆初年(1736年)开始，历时近30年，证明了包括这个公式在内的三个公式，同时求得了展开三角函数和反三角函数的6个新级数公式，著有《割圆密率捷法》一书，为我国用级数计算π开创了先河．如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值(其中P表示π的近似值)，若输入n=10，则输出的结果是(    )


A. P=4(1−13+15−17+…+117) B. P=4(1−13+15−17+…−119)
C. P=4(1−13+15−17+…+121) D. P=4(1−13+15−17+…−121)
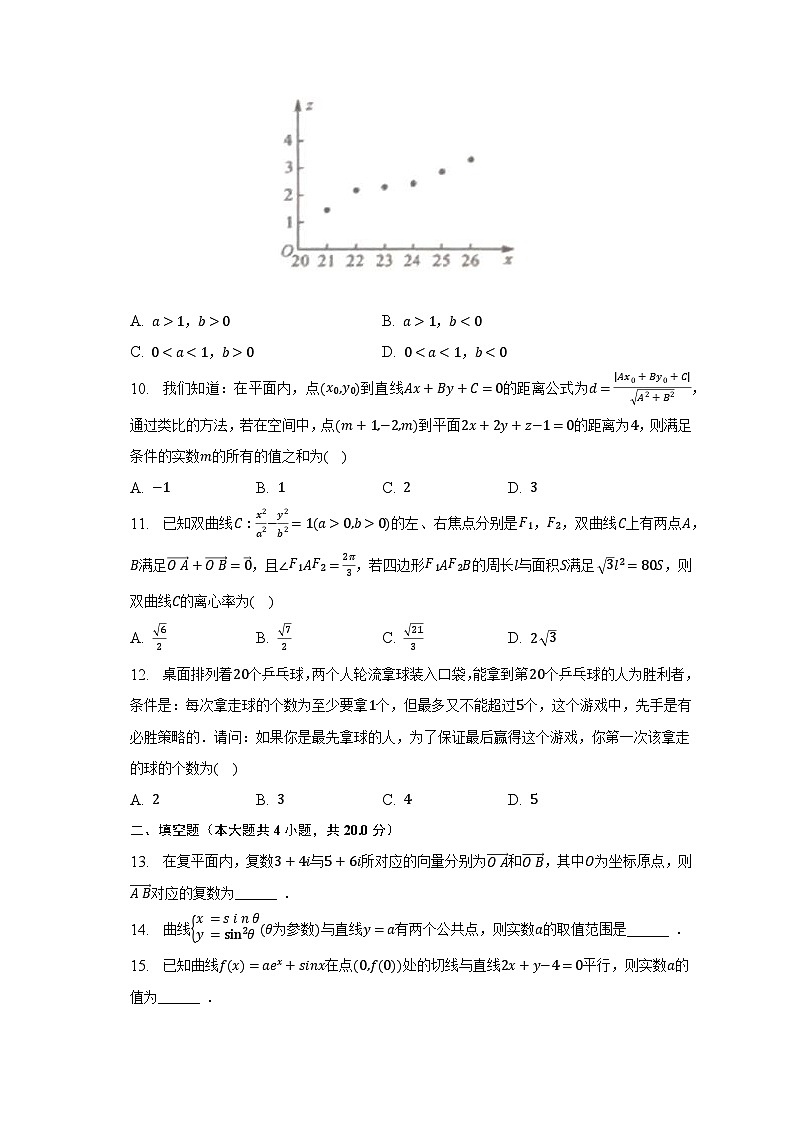
9. 一只红铃虫的产卵数y和温度x有关，现收集了6组观测数据，y(单位：个)与温度x(单位：℃)得到样本数据(xi,yi)(i=1,2,3,4,5,6)，令zi=lnyi，并将(xi,zi)绘制成如图所示的散点图．若用方程y=aebx对y与x的关系进行拟合，则(    )

A. a>1，b>0 B. a>1，bR，R−Q=( 6+ 3)−( 7+ 2)，而( 6+ 3)2=9+2 18>( 7+ 2)2=9+2 14，故R>Q，故可比较P，Q，R的大小．
【解答】
解：∵P−R= 2− ( 6− 2)=2 2− 6>0，
∴P>R，
R−Q= 6− 2−( 7− 3)=( 6+ 3)−( 7+ 2)，
而( 6+ 3)2=9+2 18，( 7+ 2)2=9+2 14，
而18>14，
∴ 6+ 3> 7+ 2，即R>Q，
综上，P>R>Q，
故选：B．
  
8.【答案】B 
【解析】解：由程序框图知：算法的功能是求P=4S=4[(−1)02×1−1+(−1)12×2−1+(−1)22×3−1…+(−1)92×10−1]的值，
∵输入n=10，∴跳出循环的i值为11，
∴输出P=4S=4[(−1)02×1−1+(−1)12×2−1+(−1)22×3−1…+(−1)92×10−1]=4(1−13+15−…−119).
故选：B．
模拟程序的运行可得算法的功能是求P=4S=4[(−1)02×1−1+(−1)12×2−1+(−1)22×3−1…+(−1)92×10−1]的值，根据条件确定跳出循环的i值，即可计算得解．
本题考查程序框图，根据框图的流程判断算法的功能是解答本题的关键，属于基础题．

9.【答案】A 
【解析】解：因为y=aebx，令z=lny，则z与x的回归方程为z=bx+lna，
根据散点图可知z与x正相关，所以b>0，
由回归直线图象，可知回归直线的纵截距大于0，即lna>0，所以a>1，
故选：A．
令z=lny，可得z与x的回归方程为z=bx+lna，根据散点图，可得z与x正相关，所以b>0，根据纵截距大于0，可得a的范围，即可得答案．
本题考查了散点图的应用，考查了非线性回归与线性回归的转化，属于基础题．

10.【答案】C 
【解析】解：平面内点(x0,y0)到直线Ax+By+C=0的距离公式d=|Ax0+By0+C| A2+B2，
类比平面内点到直线的距离公式，
可得空间中点(m+1,−2,m)到平面2x+2y+z−1=0的距离为d=|2(m+1)−2×2+m−1| 12+22+22=4，
即|3m−3|3=4，∴|m−1|=4，解得m=−3或5，
则满足条件的实数m的所有的值之和为5−3=2．
故选：C．
类比平面中的结论得到空间中的结论，再解绝对值方程即可求得所有的m的值．
本题考查类比思想，类比平面结论得到空间中的结论来求解，属于基础题．

11.【答案】A 
【解析】解：不妨设|AF1|=m，|AF2|=n(m>n)，由双曲线的定义可知，m−n=2a，则m2+n2−2mn=4a2①，又∠F1AF2=2π3，
所以由余弦定理可得m2+n2+mn=4c2②，由①②可得mn=4c2−4a23,m2+n2=8c2+4a23，
所以(m+n)2=16c2−4a23.又四边形F1AF2B为平行四边形，故四边形F1AF2B的周长l=2(m+n)，
则l2=4(m+n)2=16(4c2−a2)3，面积S=2×12× 32mn= 36(4c2−4a2)，因为 3l2=80S，所以 3×16(4c2−a2)3=80× 36×(4c2−4a2)，整理得2c2=3a2，
故双曲线C的离心率为ca= 62，
故选：A．
设|AF1|=m，|AF2|=n(m>n)，由双曲线的定义和余弦定理求得m+n，从而可得周长l=2(m+n)，再求得四边形面积S，由已知等式得a，c关系，从而得离心率．
本题考查双曲线的离心率相关问题，属于中档题．

12.【答案】A 
【解析】解：根据题意，第一次该拿走2个球，以后的取球过程中，对方取n个，自己取6−n个，
由于20−2=6×3，
则自己可以一定可以取到第20个球；
故选：A．
根据题意，根据游戏的规则，结合余数的性质，分析可得答案．
本题考查合情推理的应用，注意游戏的规则，属于基础题．

13.【答案】2+2i 
【解析】解：由题意，OA=(3,4)，OB=(5,6)，
则AB=OB−OA=(2,2)，
∴AB对应的复数为2+2i．
故答案为：2+2i．
由已知求得OA、OB的坐标，进一步可得AB的坐标，则答案可求．
本题考查复数的代数表示法及其几何意义，是基础题．

14.【答案】0