

2022-2023学年北京市大兴区八年级(下)期末数学试卷(含解析)
展开2022-2023学年北京市大兴区八年级(下)期末数学试卷
一、选择题(本大题共8小题,共16.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列各式中,不是最简二次根式的是( )
A. 3 B. 4 C. 5 D. 6
2. 已知正比例函数y=kx(k≠0)的图象经过点(1,−2),则这个正比例函数的解析式为( )
A. y=2x B. y=−2x C. y=12x D. y=−12x
3. 将直线y=2x向下平移1个单位得到的直线是( )
A. y=−2x+1 B. y=−2x−1 C. y=2x+1 D. y=2x−1
4. 下列运算中,正确的是( )
A. (−2)2=−2 B. 72=−7 C. − 52=−5 D. − (−3)2=3
5. 在▱ABCD中,若∠A+∠C=140°,则∠B的度数是( )
A. 70° B. 110° C. 120° D. 140°
6. 库各庄自宋朗开灿种植西瓜,被普为“西瓜之乡”.2023年5月28日,第35届北京大兴西瓜节开醇.某西瓜采搁园一个星期销售西瓜数量(箱)如下:
星期
−
二
三
四
五
六
H
销量(箱)
47
47
50
42
48
60
63
则这个星期该采摘园西瓜销量的众数和中位数分别是( )
A. 47.42 B. 50.48 C. 47,48 D. 50.42
7. 如图,在平面直角坐标系xOy中,四边形ABCD是菱形,∠ABC=120°,点B的坐标为(0,−3),则点A的坐标为( )
A. (−3 3,0)
B. (3 3.0)
C. (−6,0)
D. (6,0)
8. 下面的三个问题中部有两个变量:
①圆的周长y与它的半径x;
②将水箱中的水匀速放出,直至放完,水箱中的剩余水量y与放水时间x;
③汽车从A地匀速行驶到B地,汽车的剩余路程y与行驶时间x;
其中,变量y与变量x之间的函数关系可以用如图所示的图象表示的是( )
A. ①②③ B. ①② C. ①③ D. ②③
二、填空题(本大题共8小题,共16.0分)
9. 函数y=6x−2中,自变量x的取值范围是______ .
10. 若正方形面积为16,则对角线的长为______ .
11. 若一次函数的图象经过(0,4),且y随x的增大而增大,请你写出一个满足条件的一次函数的解析式______ .
12. 若点A(−2,m),B(−1,n)都在直线y=−x+1上,则m ______ n(填“>”“<”或“=”).
13. 如图,四边形ABCD是矩形,O是对角线AC与BD的交点,若AB=3,AD=4,则△COD的周长是______ .
14. 函数y=kx与y=6−x的图象如图所示,则k=______.
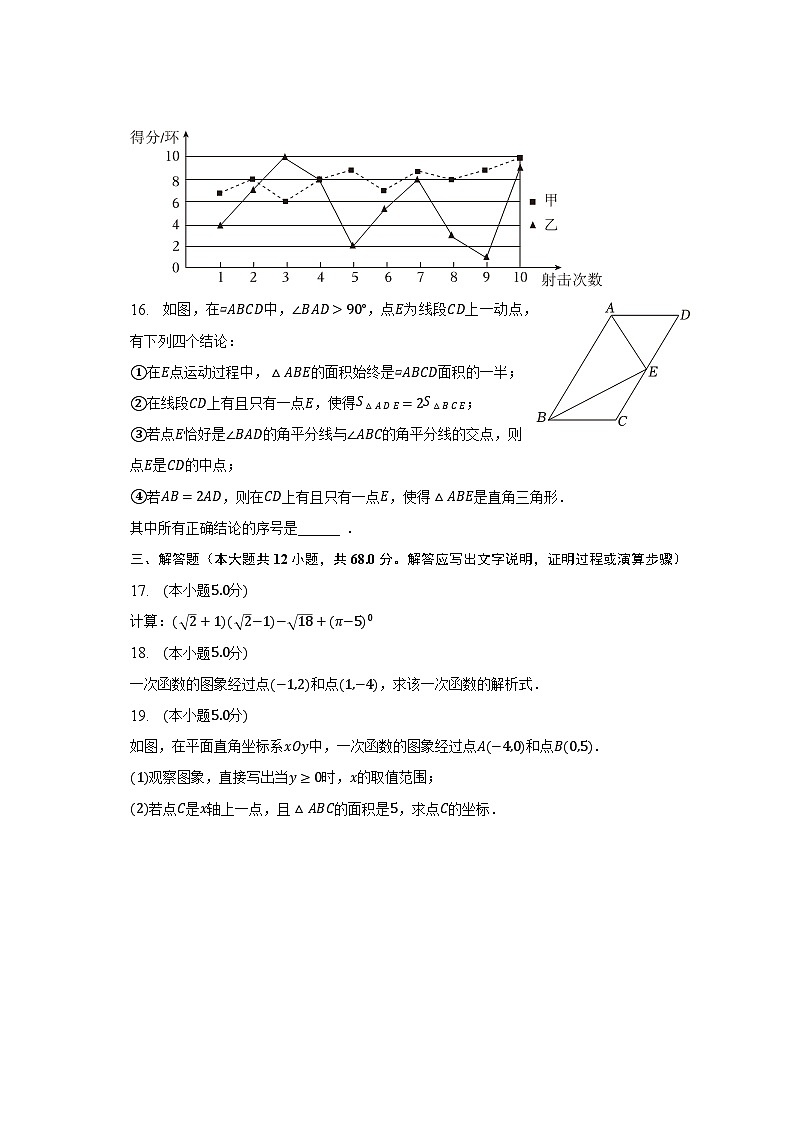
15. 甲、乙两名射击爱好者10次射击测试成绩(单位:环)的统计图如图所示.根据图中的信息,两人中发挥相对稳定的是______ .
16. 如图,在▱ABCD中,∠BAD>90°,点E为线段CD上一动点,有下列四个结论:
①在E点运动过程中,△ABE的面积始终是▱ABCD面积的一半;
②在线段CD上有且只有一点E,使得S△ADE=2S△BCE;
③若点E恰好是∠BAD的角平分线与∠ABC的角平分线的交点,则点E是CD的中点;
④若AB=2AD,则在CD上有且只有一点E,使得△ABE是直角三角形.
其中所有正确结论的序号是______ .
三、解答题(本大题共12小题,共68.0分。解答应写出文字说明,证明过程或演算步骤)
17. (本小题5.0分)
计算:( 2+1)( 2−1)− 18+(π−5)0
18. (本小题5.0分)
一次函数的图象经过点(−1,2)和点(1,−4),求该一次函数的解析式.
19. (本小题5.0分)
如图,在平面直角坐标系xOy中,一次函数的图象经过点A(−4,0)和点B(0,5).
(1)观察图象,直接写出当y≥0时,x的取值范围;
(2)若点C是x轴上一点,且△ABC的面积是5,求点C的坐标.
20. (本小题5.0分)
下面是证明三角形中位线定理的两种添加辅助线的方法,选择其中一种,完成证明.
已知:如图,△ABC中,D、E分别是AB、AC的中点.
求证:DE//BC,且DE=12BC.
方法一
证明:如图,延长DE至点F,使EF=DE,连接CF.
方法二
证明:如图,过点C作CF//AB交DE的延长线于F.
21. (本小题5.0分)
在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象由函数y=x的图象平移得到,且经过点A(3,5).
(1)求这个一次函数的解析式;
(2)当x<1时,对于x的每一个值,函数y=mx(m≠0)的值小于函数y=kx+b(k≠0)的值,直接写出m的取值范围.
22. (本小题6.0分)
呦呦、鸣鸣这对麝鹿兄妹是大兴区创建全国文明城区的吉祥物.某中学决定制作这对吉祥物的宣传条幅和展示牌,若宣传条幅的单价比展示牌的单价多2元,制作4个宣传条幅比制作5个展示牌多3元.
(1)求宣传条幅和展示牌的单价各多少元?
(2)该学校需制作宣传条幅和展示牌共200个.
①若制作展示牌m个,制作宣传条幅和展示牌共花费w元,求w与m的函数解析式;
②若展示牌的数量不超过宣传条幅数量的3倍,求该中学制作多少个展示牌时.所需费用最少?最少费用是多少?
23. (本小题5.0分)
2023年5月30日、神舟十五号和神舟十六号两个乘组六名航天员会师空间站,这是中国空间站的第二次两个乘组在轨交接.为了解某校八年级学生对航天知识的掌握情况,现从东、西两个校区八年级各随机抽取35名学生的测试成绩进行收集、整理、描述和分析.下面给出了部分信息:
a.东校区八年级航天知识测试得分的频数分布表(数据分成6组:65.0≤x<70.0,70.0≤x<75.0,75.0≤x<80.0,80.0≤x<85.0,85.0≤x<90.0,90.0≤x≤100);
东校区八年级航天知识测试得分
频数
65.0≤x<70.0
8
70.0≤x<75.0
12
75.0≤x<80.0
m
80.0≤x<85.0
5
85.0≤x<90.0
2
90.0≤x≤100
1
合计
35
b.东校区八年级航天知识测试得分在70.0≤x<75.0这一组的是:
70.2 70.5 70.7 71.0 71.0 71.1 71.2 71.8 71.9 72.5 73.8 74.5;
e.东、西两个校区八年级航天知识测试得分的平均数,中位数如下:
平均数
中位数
东校区八年级
72.8
n
西校区八年级
73
73.4
根据以上信息,回答下列问题:
(1)写出表1中m的值及表2中n的值;
(2)在东校区八年级抽取的学生中,记航天知识测试得分高于他们的平均分的人数为P1,在西校区八年级抽取的学生中,记航天知识测试得分高于他们的平均分的人数为P2比较P1P2的大小,并说明理由;
(3)若东校区八年级共有350名学生参加航天知识测试,估计东校区八年级本次航天知识测试80分以上(含80分)有多少人?
24. (本小题6.0分)
有这样一个问题:探究函数y=|x|−2的图象与性质.
小青根据学习函数的经验,对该函数的图象与性质进行了探究,下面是小青的探究过程,请补充完整:
(1)函数y=|x|−2的自变量x的取值范围是______ .
(2)下表是y与x的几组对应值:
r
…
−4
−3
−2
−1
0
1
2
3
4
…
y
…
2
1
0
−1
−2
−1
0
1
m
…
写出表中m的值______ ;
(3)如图,在平面直角坐标系xOy中,描出以上表中各组对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)根据画出的函数图象,直接写出该函数的一条性质.
25. (本小题6.0分)
如图,▱ABCD中,∠BAC=90°,E,F分别是BC,AD的中点
(1)求证:四边形AECF是菱形;
(2)如果AB=2,BC=4,求四边形AECF的面积.
26. (本小题6.0分)
【阅读材料】小华根据学习“二次根式“及”乘法公式“积累的经验,通过“由特殊到一般”的方法,探究”当a>0、b>0时, ab与a+b的大小关系”.
下面是小单的深究过程:
①具体运算,发现规律:
当a>0,b>0时,
特例1:若a+b=2,则2 ab≤2;
特例2:若a+b=3,则2 ab≤3;
特例3:若a+b=6,则2 ab≤6.
②观察、归纳,得出猜想:当a>0,b>0时,2 ab≤a+b.
③证明猜想:
当a>0,b>0时,
∵( a− b)2=a−2 ab+b≥0,
∴a+b≥2 ab,
∴2 ab≤a+b.
当且仅当a=b时,2 ab=a+b.
请你利用小华发现的规律解决以下问题:
(1)当x>0时,x+1x的最小值为______
(2)当x<0时,−x−2x的最小值为______ ;
(3)当x<0时,求x2+2x+6x的最大值.
27. (本小题7.0分)
如图,四边形ABCD是正方形,过点D在正方形ABCD的外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM,DM,线段AM交直线DE于点N,设∠CDE=α.
(1)补全图形:
(2)当α=20°时,直接写出∠AND的度数;
(3)当0°<α<45°时,用等式表示线段DN,AN与MN的数量关系,并证明.
28. (本小题7.0分)
在平面直角坐标系xOy中,对于任意两点M(x1,y1),N(x2,y2)我们将|x1−x2|+|y1−y2|称为点M与点N的“直角距离”,记作dMN.
例如:点M(−2,4)与点N(5,3)的“直角距离”dMN=|−2−5|+|4−3|=8.
(1)已知点P1(1,3),P2(−2,−3),P3(−52,32),在这三个点中,与原点O的“直角距离”等于4的点是______ ;
(2)若直线y=54x+b上恰好有两个点与原点O的“直角距离”等于4,直接写出b的取值范围;
(3)已知点A(m,2),B(m+5,2),若线段AB上有且只有一点C,使得dCO=4,直接写出m的取值范围.
答案和解析
1.【答案】B
【解析】解:A、 3是最简二根式,故A不符合题意;
B、 4=2,故B符合题意;
C、 5是最简二根式,故C不符合题意;
D、 6是最简二根式,故D不符合题意;
故选:B.
根据最简二次根式的定义:被开方数中不含能开得尽方的因数或因式,被开方数中不含分母,逐一判断即可解答.
本题考查了最简二次根式,熟练掌握最简二次根式的定义是解题的关键.
2.【答案】B
【解析】解:∵正比例函数y=kx经过点(1,−2),
∴−2=1⋅k,
解得:k=−2,
∴这个正比例函数的解析式为:y=−2x.
故选B.
利用待定系数法把(1,−2)代入正比例函数y=kx中计算出k即可得到解析式.
此题主要考查了待定系数法求正比例函数解析式,题目比较简单,关键是能正确代入即可.
3.【答案】D
【解析】解:由“上加下减”的原则可知,直线y=2x向下平移1个单位,得到直线是:y=2x−1.
故选:D.
平移时k的值不变,只有b的值发生变化,而b值变化的规律是“上加下减”.
本题考查的是一次函数的图象与几何变换,熟知“上加下减”的原则是解答此题的关键.
4.【答案】C
【解析】解:∵ (−2)2=|−2|=2,
∴A选项的计算不正确,不符合题意;
∵ 72=7,
∴B选项计算不正确,不符合题意;
∵− 52=−5,
∴C选项计算正确,符合题意;
∵− (−3)2=−3,
∴D选项的计算不正确,不符合题意.
故选:C.
利用二次根式的性质对每个选项进行逐一判断即可得出结论.
本题主要考查了二次根式的性质与化简,熟练掌握二次根式的性质是解题的关键.
5.【答案】B
【解析】解:∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵∠A+∠C+∠B+∠D=360°,∠A+∠C=140°,
∴∠B+∠D=220°,
∴2∠B=220°,
∴∠B=110°,
故选:B.
由平行四边形的性质得∠B=∠D,由∠A+∠C+∠B+∠D=360°,∠A+∠C=140°,得2∠B=220°,则∠B=110°,于是得到问题的答案.
此题重点考查平行四边形的性质、四边形的内角和等于360°等知识,证明∠B=∠D并且求得∠B+∠D=220°是解题的关键.
6.【答案】C
【解析】解:将这7个数据从小到大排列为:42,47,47,48,50,60,63,
所以众数为47,中位数为48.
故选:C.
将这组数据重新排列,再根据众数和中位数的定义求解即可.
本题属于基础题,考查了确定一组数据的中位数和众数的能力.一组数据中出现次数最多的数据叫做众数.求一组数据的众数的方法:找出频数最多的那个数据,若几个数据频数都是最多且相同,此时众数就是这多个数据.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.
7.【答案】A
【解析】解:∵点B的坐标为(0,−3),
∴OB=3,
∵四边形ABCD是菱形,∠ABC=120°,
∴∠ABO=12∠ABC=60°,
∵∠AOB=90°,
∴OA=OB⋅tan60°=3 3,
∴A(−3 3,0),
故选:A.
由B点坐标求得OB,再解Rt△OAB,求得OA,于是得到结论.
本题主要考查了直角坐标系中点的坐标,菱形的性质,解直角三角形,关键是解直角三角形求得对角线的长度.
8.【答案】D
【解析】解:①:圆的周长y与它的半径x函数关系为:y=2πx,为正比例函数,故不符合题意;
②:将水箱中的水匀速放出,直至放完,水箱中的剩余水量y与放水时间x,y随x的增大而减少,故符合题意;
③:汽车从A地匀速行驶到B地,汽车的剩余路程y与行驶时间x,剩余路程等于总路程减行驶的路程(速度×时间),故符合题意;
故选D.
根据图象在第一象限为一次函数并y随x的增大而减少,逐次作答.
本题考查函数关系式及一次函数图象对应关系,解题的关键是对图象与关系式之间关系的熟练运用.
9.【答案】x≠2
【解析】解:由题意得:x−2≠0,
解得:x≠2,
故答案为:x≠2.
根据分母不为0可得x−2≠0,然后进行计算即可解答.
本题考查了函数自变量的取值范围,熟练掌握分母不为0是解题的关键.
10.【答案】4 2
【解析】解:设正方形的边长为x,
根据题意得x2=16,解得x1=4,x2=−4(舍去),
即正方形的边长为4,
所以正方形的对角线的长为4 2.
故答案为:4 2.
设正方形的边长为x,利用正方形的面积公式得到x2=16,解得x=4,然后根据等腰直角三角形的性质计算正方形的对角线的长.
本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.
11.【答案】y=x+4(答案不唯一)
【解析】解:由于y随x增大而增大,则k>0,取k=1;
设一次函数的关系式为y=x+b;
代入(0,4)得:b=4;
则一次函数的解析式为:y=x+4(k为正数即可).
故答案为:y=x+4(答案不唯一).
设一次函数的解析式为y=kx+b(k>0),再把(0,4)代入得出b的值即可得出结论.
本题考查的是一次函数的性质,此题属开放性题目,答案不唯一.
12.【答案】>
【解析】解:∵−1<0,
∴y随x的增大而减小,
又∵点A(−2,m),B(−1,n)都在直线y=−x+1上,且−2<−1,
∴m>n.
故答案为:>.
由−1<0,利用一次函数的性质,可得出y随x的增大而减小,再结合−2<−1,即可得出m>n.
本题考查了一次函数的性质,牢记“k>0,y随x的增大而增大;k<0,y随x的增大而减小”是解题的关键.
13.【答案】8
【解析】解:∵四边形ABCD是平行四边形,AB=3,AD=4,
∴∠BAD=90°,OA=OC,OB=OD,AC=BD,BC=AD=4,CD=AB=3,
∴AC=BD= AB2+AD2=5,
∴OC=OD=52,
∵△COD的周长=OC+OD+CD=8.
故答案为:8.
根据矩形的性质和勾股定理求出OC,OD,根据三角形的周长公式即可求得答案.
本题考查了矩形的性质,勾股定理,三角形的周长公式,熟练掌进行的性质是解题的关键.
14.【答案】2
【解析】解:∵一次函数y=6−x与y=kx图象的交点横坐标为2,
∴y=6−2,
解得:y=4,
∴交点坐标为(2,4),
代入y=kx,2k=4,解得k=2.
故答案为2.
首先根据一次函数y=6−x与y=kx图象的交点横坐标为2,代入一次函数y=6−x求得交点坐标为(2,4),然后代入y=kx求得k值即可.
本题考查了两条直线相交问题,解题的关键是交点坐标适合y=6−x与y=kx两个解析式.
15.【答案】甲
【解析】解:根据折线图可知,甲的波动小,乙的波动大,
所以两人中发挥相对稳定的是甲.
故答案为:甲.
根据折线图即可看出,甲的波动小,乙的波动大,即可得出答案.
此题主要考查了方差,关键是掌握方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
16.【答案】①②③
【解析】解:作EF⊥AB于点F,
∵四边形ABCD是平行四边形,
∴S▱ABCD=AB⋅EF,
∴S△ABE=12AB⋅EF=12S▱ABCD,
故①正确;
∵S△ADE=12DE⋅EF,S△BCE=12CE⋅EF,且S△ADE=2S△BCE,
∴12DE⋅EF=2×12CE⋅EF,
∴DE=2CE,
∴在线段CD上有且只有一点E,使得S△ADE=2S△BCE,
故②正确;
∵AB//CD,AD=BC,
∴∠DEA=∠EAB,∠CEB=∠EBA,
∵点E恰好是∠BAD的角平分线与∠ABC的角平分线的交点,
∴∠DAE=∠EAB,∠CBE=∠EBA,
∴∠DEA=∠DAE,∠CEB=∠CBE,
∴ED=AD,EC=BC,
∴ED=EC,
∴点E是CD的中点,
故③正确;
取AB的中点G,连接EG,
∵AB=2AG=2BG,AB=2AD=2BC,
∴AG=AD,BG=BC,
当GE//AD时,则GE//BC,
∴四边形AGED和四边形BGEC都是菱形,
∴EG=AG=BG,
∴∠GEA=∠GAE,∠GEB=∠GBE,
∴∠AEB=∠GEA+∠GEB=12×180°=90°,
∴△ABE是直角三角形,
∵∠GED=∠BAD>90°,
∴GE与CD不垂直,
∴在CD上可能还存在点E′,使E′G=EG=AG=BG,
同理可证明△ABE′是直角三角形,
故④不正确,
故答案为:①②③.
作EF⊥AB于点F,则S△ABE=12AB⋅EF=12S▱ABCD,可判断①正确;由S△ADE=12DE⋅EF,S△BCE=12CE⋅EF,且S△ADE=2S△BCE,得12DE⋅EF=2×12CE⋅EF,所以DE=2CE,可知在线段CD上有且只有一点E,使得S△ADE=2S△BCE,可判断②正确;由AB//CD,得∠DEA=∠EAB,∠CEB=∠EBA,而∠DAE=∠EAB,∠CBE=∠EBA,所以∠DEA=∠DAE,∠CEB=∠CBE,则ED=AD,EC=BC,所以,可判断③正确;取AB的中点G,连接EG,可证明当GE//AD时,则EG=AG=BG,可证明△ABE是直角三角形,由∠GED=∠BAD>90°,可知GE与CD不垂直,因此在CD上可能还存在点E′,使E′G=EG=AG=BG,同理可证明△ABE′是直角三角形,可判断④不正确,于是得到问题的答案.
此题重点考查平行四边形的性质、平行线的性质、等腰三角形的判定、菱形的判定与性质等知识,此题综合性较强,难度较大.
17.【答案】解:由题意得,
原式=2−1−3 2+1
=2−3 2.
【解析】依据题意,根据平方差公式及实数的性质进行运算即可得解.
本题考查了实数的性质,解题时需要熟练掌握并准确计算.
18.【答案】解:设该一次函数的解析式为y=kx+b(k≠0),
∵y=kx+b(k≠0)的图象过点(−1,2)和点(1,−4),
2=−k+b−4=k+b,
解方程组得:k=−3b=−1,
∴该一次函数的解析式为y=−3x−1.
【解析】将点(−1,2)和点(1,−4)分别代入一次函数的解析式y=kx+b(k、b是常数,且k≠0),列出关于k、b的二元一次方程组;然后通过解方程组求得k、b的值.即利用待定系数法求一次函数的解析式.
本题考查了待定系数法求一次函数的解析式.在设解析式时,注意注明一次函数解析式y=kx+b中的k、b是常数,且k≠0.
19.【答案】解:(1)当y≥0时,x的取值范围是x≥−4;
(2)设点C(m,0),
∴S△ABC=12AC⋅OB=12|m+4|×5,
∵△ABC的面积是5,
∴12|m+4|×5=5,
解得m=−6或m=−2,
∴点C的坐标为(−6,0)或(−2,0).
【解析】(1)由图象即可求解.
(2)根据△ABC的面积即可求得C的坐标.
本题主要考查一次函数图象上点的坐标特征,三角形面积,数形结合是解题的关键.
20.【答案】证明:方法一:∵D、E分别是AB、AC的中点,
∴AD=BD,AE=CE,
在△ADE与△CFE中,
AE=CE∠AED=∠CEFDE=EF,
∴△ADE≌△CFE(SAS),
∴∠ADE=∠F,AD=CF,
∴CF//AB,CF=BD,
∴四边形BCFD是平行四边形,
∴DF=BC,DF//BC,
∴DE=12DF=12BC;
方法二:∵D、E分别是AB、AC的中点,
∴AD=BD,AE=CE,
∵CF//AB,
∴∠ADE=∠F,
在△ADE与△CFE中,
∠AED=∠CEF∠ADE=∠FAE=CE,
∴△ADE≌△CFE(AAS),
∴AD=CF,DE=FE,
∴CF=BD,
∴四边形BCFD是平行四边形,
∴DF=BC,DF//BC,
∴DE=12DF=12BC.
【解析】方法一:由中点可得AD=BD,AE=CE,利用SAS可证得△ADE≌△CFE,则有∠ADE=∠F,AD=CF,从而有CF//AB,CF=BD,可判定四边形BCFD是平行四边形,即有DF=BC,DF//BC,从而可求证DE=12BC;
方法二:由中点可得AD=BD,AE=CE,由平行线的性质可得∠ADE=∠F,利用AAS可证得△ADE≌△CFE,则有AD=CF,DE=FE,从而有CF=BD,可判定四边形BCFD是平行四边形,即有DF=BC,DF//BC,从而可求证DE=12BC;
本题主要考查三角形的中位线定理,全等三角形的判定与性质,解答的关键是作出正确的辅助线.
21.【答案】解:(1)∵一次函数y=kx+b(k≠0)的图象由函数y=x的图象平移得到,
∴k=1,
∵一次函数y=x+b的图象经过点A(3,5),
∴3+b=5.
∴b=2.
∴这个一次函数的解析式为y=x+2;
(2)当x=1时,y=x+2=1+2=3;
∴将(1,3)代入y=mx,
解得:m=3,
当x<1时,对于x的每一个值,函数y=mx(m≠0)的值小于一次函数y=kx+b的值,
∴m≤3,
∴m大于y=x+2的系数k,且m≥1,
∴1≤m≤3.
【解析】(1)先根据直线平移时k的值不变得出k=1,再将点A(3,5)代入y=x+b,求出b的值,即可得到一次函数的解析式;
(2)根据图象即可求得.
本题考查了一次函数图象与几何变换,一次函数与系数的关系,数形结合是解题的关键.
22.【答案】解:(1)设展示牌的单价为x元,则宣传条幅的单价为(x+2)元,
根据题意得:4(x+2)−5x=3,
解得x=5,
∴x+2=7.
答:展示牌的单价为5元,宣传条幅的单价为7元;
(2)①由题意可得,
w=5m+7(200−m)=−2m+1400,
即w与m的函数解析式是w=−2m+1400;
②∵展示牌的数量不超过宣传条幅数量的3倍,
∴m≤3(200−m),
解得m≤150,
∵w=−2m+1400,
∴w随m的增大而减小,
∴当m=150时,w取得最小值,此时w=1100元,
答:制作展示牌为150个时,所需费用最少,最少费用是1100元.
【解析】(1)根据宣传条幅的单价比展示牌的单价多2元,制作4个宣传条幅比制作5个展示牌多3元,可以列出相应的方程,然后求解即可;
(2)①根据(1)中的结果和题意,可以写出w与m的函数解析式;
②根据展示牌的数量不超过宣传条幅数量的3倍,可以求得m的取值范围,再根据一次函数的性质,即可得到该中学制作多少个展示牌时.所需费用最少,最少费用是多少.
本题考查一元一次方程的应用、一次函数的应用,解答本题的关键是明确题意,列出相应的方程,求出相应的函数解析式,利用一次函数的性质求最值.
23.【答案】解:(1)m=35−(8+12+5+2+1)=7,
将东校区八年级35名学生的测试成绩按从小到大的顺序排列,第18个数落在第二组,即70.0≤x<75.0,
∵第一组有8人,第二组12名学生的成绩从小到大排列为70.2 70.5 70.7 71.0 71.0 71.1 71.2 71.8 71.9 72.5 73.8 74.5
∴中位数n=72.5;
(2)P1
由于西校区八年级抽取的35名学生的航天知识测试得分的平均数是73,中位数是73.4,
因此,所抽取的35名学生的航天知识测试得分在73及以上的占比多于一半,也就是P2的值大于等于18,
所以P1
答:东校区八年级本次航天知识测试80分以上(含80分)有80人.
【解析】(1)根据各组频数之和等于数据总数可得m的值,根据中位数的定义可得n的值;
(2)求出P1的值,根据中位数的意义判断P2的范围,即可比较大小;
(3)用350乘以样本中东校区八年级本次航天知识测试80分以上(含80分)所占的比例即可.
本题考查了频数分布表,从统计表中获取有用信息是解决问题的关键,也考查了平均数,中位数,利用样本估计总体等知识.
24.【答案】x为任意实数 2
【解析】解:(1)在函数y=|x|−2中,自变量x的取值范围是x为任意实数,
故答案为:x为任意实数;
(2)当x=4时,y=|x|−2=2,
∴m=2,
故答案为:2;
(3)函数图象如图所示:
(4)根据图象可知,当x>0时,y随着x的增大而增大.
(1)根据解析式即可确定自变量取值范围;
(2)当x=4代入解析式即可;
(3)根据表格描点,连线即可画出函数图象;
(4)根据图象即可确定.
本题考查了一次函数的图象和性质,数形结合是解题的关键.
25.【答案】证明:(1)∵在▱ABCD中,
∴BC=AD,BC//AD,
又∵E,F分别是边BC,AD的中点,
∴EC=12BC,AF=12AD,
∴EC=AF,且EC//AF
∴四边形AECF为平行四边形.
在Rt△ABC中,∠BAC=90°,E是BC边中点,
∴AE=EC,
∴四边形AECF是菱形;
(2)∵∠BAC=90°,AB=2,BC=4,
∴AC= BC2−AB2=2 3
∴S△ABC=12AB×AC=2 3
∵点E是BC的中点,
∴S△AEC=12S△ABC= 3
∵四边形AECF是菱形
∴四边形AECF的面积=2S△AEC=2 3
【解析】(1)由平行四边形的性质可得BC=AD,BC//AD,由中点的性质可得EC=AF,可证四边形AECF为平行四边形,由直角三角形的性质可得AE=EC,即可得结论;
(2)由勾股定理可求AC的长,可求S△ABC=12AB×AC=2 3,即可求四边形AECF的面积.
本题考查了菱形的判定和性质,直角三角形的性质,三角形的面积公式,熟练运用菱形的判定是本题的关键.
26.【答案】2 2 2
【解析】解:(1)∵x>0,
∴x+1x≥2 x⋅1x=2,
∴x+1x的最小值为2,
故答案为:2;
(2)∵x<0,
∴−x>0,
∴−x−2x=(−x)+(−2x)≥2 (−x)⋅(−2x)=2 2,
∴−x−2x的最小值为2 2,
故答案为:2 2;
(3)∵x<0,
∴−x>0,
∴x2+2x+6x
=x+6x+2
=−(−x−6x)+2
≤−2 6+2,
∴x2+2x+6x的最大值为2−2 6.
(1)根据阅读材料直接可得x+1x≥2 x⋅1x=2;
(2)根据x的取值范围,将所求的式子变形为−x−2x=(−x)+(−2x),再结合阅读材料求解即可;
(3)先变量分离已知式子,再由x的取值范围,将所求式子变形为−(−x−6x)+2,结合(2)求解即可.
本题考查基本不等式,熟练掌握二次根式的性质,完全平方公式的特点,能够准确地将所求的式子变形是解题的关键.
27.【答案】解:(1)如图,作点C关于直线DE的对称点为M,连接CM,AM,DM,线段AM交直线DE于点N.
(2)∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∵点M与点C关于直线DE对称,
∴直线DE垂直平分CM,
∴MD=CD,
∵∠CDE=α=20°,
∴∠MDE=∠CDE=20°,
∴∠CDM=∠MDE+∠CDE=20°+20°=40°,
∴∠ADM=∠ADC+∠CDM=90°+40°=130°,
∵AD=MD,
∴∠DMA=∠DAM=12×(180°−130°)=25°,
∴∠AND=∠MDE+∠DMA=20°+25°=45°,
∴∠AND的度数是45°.
(3)AN=MN+ 2DN,
证明:如图,设CM交DE于点O,在AN上截取AF=MN,连接DF,
在△ADF和△MDN中,
AD=MD∠DAF=∠DMNAF=MN,
∴△ADF≌△MDN(SAS),
∴DF=DN,∠ADF=∠MDN,
∵∠MDN=∠CDE,
∴∠ADF=∠CDE,
∴∠FDN=∠CDF+∠CDE=∠CDF+∠ADF=∠ADC=90°,
∴FN= DF2+DN2= 2DN2= 2DN,
∵AN=AF+FN,AF+FN=MN+ 2DN,
∴AN=MN+ 2DN.
【解析】(1)作点C关于直线DE的对称点为M,连接CM,AM,DM,线段AM交直线DE于点N,画出相应的图形即可;
(2)由正方形的性质得AD=CD,∠ADC=90°,由直线DE垂直平分CM,得MD=CD,因为∠CDE=α=20°,所以∠MDE=∠CDE=20°,则∠CDM=∠MDE+∠CDE=40°,所以∠ADM=∠ADC+∠CDM=130°,由AD=MD,得∠DMA=∠DAM=25°,则∠AND=∠MDE+∠DMA=45°;
(3)设CM交DE于点O,在AN上截取AF=MN,连接DF,可证明△ADF≌△MDN,得DF=DN,∠ADF=∠MDN,而∠MDN=∠CDE,所以∠ADF=∠CDE,即可推导出∠FDN=∠ADC=90°,所以FN= DF2+DN2= 2DN,则AN=MN+ 2DN.
此题重点考查正方形的性质、轴对称的性质、等腰三角形的性质、三角形的一个外角等于与它不相邻的两个内角的和、等腰直角三角形的判定与性质、勾股定理等知识,此题综合性强,难度较大,属于考试压轴题.
28.【答案】P1,P3
【解析】解:(1)∵dP1O=|1−0|+|3−0|=4,
dP2O=|−2−0|+|−3−0|=5≠4,
dP3O=|−52−0|+|32−0|=4,
∴这三个点中,与原点O的“直角距离”等于4的点是P1,P3,
故答案为:P1,P3;
(2)根据“直角距离”公式可以求出在x坐标轴上到原点的“直角距离”等于4的点的坐标为(−4,0)和(4,0),
当直线y=54x+b与x轴的交点在(−4,0)右侧和(4,0)左侧时,这条直线上恰好有两个点与原点O的“直角距离”等于4,
当y=54x+b过点(−4,0)时,−54×(−4)+b=0,b=5,
当y=54x+b过点(4,0)时,54×4+b=0,b=−5,
∴直线y=54x+b上恰好有两个点与原点O的“直角距离”等于4时,b的取值范围为−5
∴线段AB上的点C的纵坐标为2,
当点C的横坐标为−2或2时,点C与原点O的“直角距离”等于4,
当−2
(2)在平面直角坐标系中找出到原点的“直角距离”等于4的点,当直线y=54x+b与x轴的交点在(−4,0)右侧和(4,0)左侧时,这条直线上恰好有两个点与原点O的“直角距离”等于4,把这两个点分别代入求出b值即可求出b的取值范围;
(3)根据“直角距离”的定义求出在直线AB上与原点O的“直角距离”等于4的点C的坐标,然后根据线段AB上有且只有一点C确定线段AB的位置,列出关于m的不等式组即可求出m的取值范围.
本题是一次函数综合题,主要考查新定义问题,函数的取值范围等知识点,深入理解题意,理解“直角距离”的意义和求法是解决问题的关键.
2023-2024学年北京市大兴区八年级(上)期末数学试卷(含解析): 这是一份2023-2024学年北京市大兴区八年级(上)期末数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2022-2023学年北京市大兴区魏善庄中学八年级(下)期末数学试卷(含答案解析): 这是一份2022-2023学年北京市大兴区魏善庄中学八年级(下)期末数学试卷(含答案解析),共14页。试卷主要包含了在平面直角坐标系中,点P在,五边形的内角和为等内容,欢迎下载使用。
2022-2023学年北京市大兴区八年级(下)期末数学试卷(含答案解析): 这是一份2022-2023学年北京市大兴区八年级(下)期末数学试卷(含答案解析),共20页。试卷主要包含了下列运算中,正确的是,42B,下面的三个问题中部有两个变量等内容,欢迎下载使用。












