2022-2023学年广东省深圳实验学校八年级（下）期末数学试卷（含解析）

这是一份2022-2023学年广东省深圳实验学校八年级（下）期末数学试卷（含解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年广东省深圳实验学校八年级（下）期末数学试卷
一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
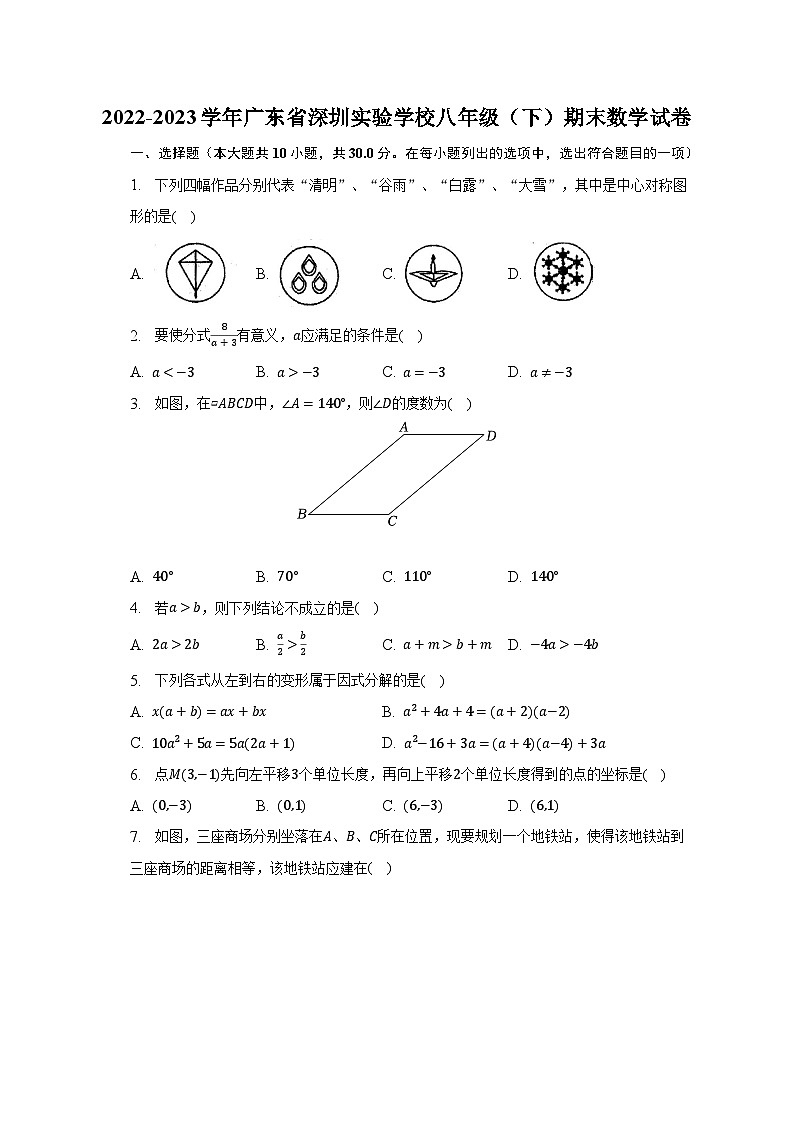
1. 下列四幅作品分别代表“清明”、“谷雨”、“白露”、“大雪”，其中是中心对称图形的是(    )
A. B. C. D.
2. 要使分式8a+3有意义，a应满足的条件是(    )
A. a−3 C. a=−3 D. a≠−3
3. 如图，在▱ABCD中，∠A=140°，则∠D的度数为(    )

A. 40° B. 70° C. 110° D. 140°
4. 若a>b，则下列结论不成立的是(    )
A. 2a>2b B. a2>b2 C. a+m>b+m D. −4a>−4b
5. 下列各式从左到右的变形属于因式分解的是(    )
A. x(a+b)=ax+bx B. a2+4a+4=(a+2)(a−2)
C. 10a2+5a=5a(2a+1) D. a2−16+3a=(a+4)(a−4)+3a
6. 点M(3,−1)先向左平移3个单位长度，再向上平移2个单位长度得到的点的坐标是(    )
A. (0,−3) B. (0,1) C. (6,−3) D. (6,1)
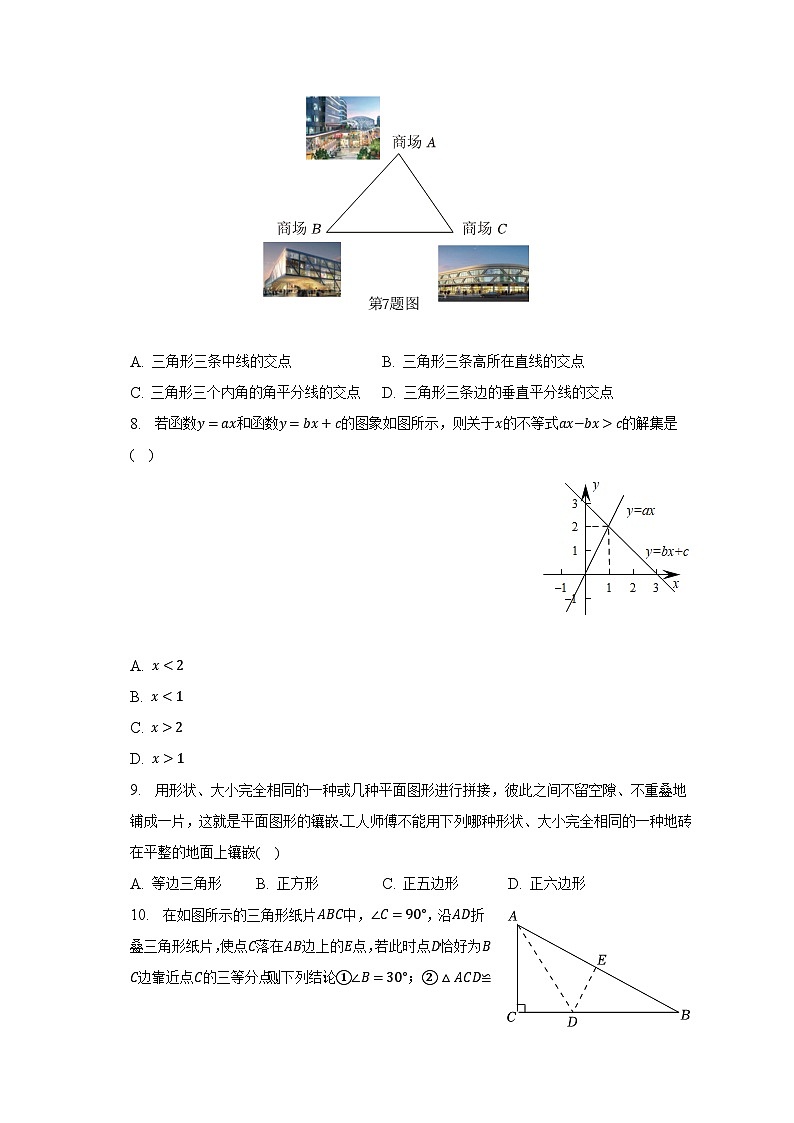
7. 如图，三座商场分别坐落在A、B、C所在位置，现要规划一个地铁站，使得该地铁站到三座商场的距离相等，该地铁站应建在(    )

A. 三角形三条中线的交点 B. 三角形三条高所在直线的交点
C. 三角形三个内角的角平分线的交点 D. 三角形三条边的垂直平分线的交点
8. 若函数y=ax和函数y=bx+c的图象如图所示，则关于x的不等式ax−bx>c的解集是(    )



A. x1
9. 用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，这就是平面图形的镶嵌.工人师傅不能用下列哪种形状、大小完全相同的一种地砖在平整的地面上镶嵌(    )
A. 等边三角形 B. 正方形 C. 正五边形 D. 正六边形
10. 在如图所示的三角形纸片ABC中，∠C=90°，沿AD折叠三角形纸片，使点C落在AB边上的E点，若此时点D恰好为BC边靠近点C的三等分点，则下列结论：①∠B=30°；②△ACD≌△BED；③DE垂直平分AB；④S△ABC= 3AC2，其中正确的是(    )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
二、填空题（本大题共5小题，共15.0分）
11. 分解因式：x2−36= ______ ．
12. 正八边形每个外角的度数为______ ．
13. 若分式x2−4x+1的值为零，则x的值是______ ．
14. 如图，在△ABC中，两条角平分线相交于点P，过点P作PD⊥BC于点D，若PD=1，△ABC的周长为12，则△ABC的面积为______ ．
15. 关于x的不等式组x−a>02(x−1)≥3x−1恰有3个整数解，那么a的取值范围为______ ．
三、解答题（本大题共7小题，共56.0分。解答应写出文字说明，证明过程或演算步骤）
16. (本小题8.0分)
解不等式组5x+2>4(x+1)12x−1≤5−32x．
17. (本小题8.0分)
先化简，再求值：x2x2−1÷(1x−1+1)，其中x=2．
18. (本小题8.0分)
解方程：2+1x−3=2−x3−x．
19. (本小题8.0分)
已知：如图，E、F是▱ABCD对角线AC上的两点．

(1)若AE=CF，求证：四边形BFDE是平行四边形；
(2)若DE⊥AC，BF⊥AC，垂足分别为E、F，∠EDF=35°，求∠FBE的度数．
20. (本小题8.0分)
某学校为丰富大课间的体育活动，决定购买甲、乙两种型号的篮球.购买时发现，甲种篮球的单价比乙种篮球单价多20元，且用900元购买甲种篮球的个数与720元购买乙种篮球的个数相同．
(1)求甲、乙两种篮球的单价各是多少元？
(2)学校准备购买甲、乙两种篮球共16个，且购买的总费用不超过1500元，求最多可以购买多少个甲种篮球．
21. (本小题8.0分)
如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，△ABC的顶点均在格点上，在建立平面直角坐标系后，点C的坐标为(−2,−1)．

(1)将△ABC向上平移6个单位得到△A1B1C1，画出△A1B1C1；
(2)以(0,−1)为对称中心，画出△ABC关于该点对称的△A2B2C2；
(3)经探究发现，△A1B1C1和△A2B2C2成中心对称，则对称中心坐标为______ ；
(4)已知点P为x轴上不同于O、D的动点，当PA+PC= ______ 时，∠OPC=∠DPA．
22. (本小题8.0分)
问题情境：在学习《图形的平移和旋转》时，数学兴趣小组遇到这样一个问题：如图1，点D为等边△ABC的边BC上一点，将线段AD绕点A逆时针旋转60°得到线段AE，连接CE．

(1)【猜想证明】试猜想BD与CE的数量关系，并加以证明；
(2)【探究应用】如图2，点D为等边△ABC内一点，将线段AD绕点A逆时针旋转60°得到线段AE，连接CE，若B、D、E三点共线，求证：EB平分∠AEC；
(3)【拓展提升】如图3，若△ABC是边长为2的等边三角形，点D是线段BC上的动点，将线段AD绕点D顺时针旋转60°得到线段DE，连接CE.点D在运动过程中，△DEC的周长最小值= ______ (直接写答案)．
答案和解析

1.【答案】D 
【解析】解：选项A、B、C都不能找到这样的一个点，使图形绕某一点旋转180°后与原来的图形重合，所以不是中心对称图形．
选项D能找到这样的一个点，使图形绕某一点旋转180°后与原来的图形重合，所以是中心对称图形．
故选：D．
根据中心对称图形的概念判断．把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形．
本题考查的是中心对称图形，中心对称图形是要寻找对称中心，旋转180度后与自身重合．

2.【答案】D 
【解析】解：∵分式8a+3有意义，
∴a+3≠0，
解得a≠−3，
∴a应满足的条件是a≠−3．
故选：D．
根据分式有意义的条件是分母不等于零，可得a+3≠0，据此求出a应满足的条件即可．
此题主要考查了分式有意义的条件，解答此题的关键是要明确：分式有意义的条件是分母不等于零．

3.【答案】A 
【解析】解：∵四边形ABCD是平行四边形，
∴∠A+∠D=180°，
∵∠A=140°，
∴∠D=40°，
故选：A．
根据平行四边形的邻角互补，即可得出答案．
此题主要考查了平行四边形的性质，灵活的应用平行四边形的性质是解决问题的关键．

4.【答案】D 
【解析】解：A、∵a>b，∴2a>2b，正确，不符合题意；
B、∵a>b，∴a2>b2，正确，不符合题意；
C、∵a>b，∴a+m>b+m，正确，不符合题意；
D、∵a>b，∴−4a1时，ax>bx+c，
即x>1时，ax−bx>c，
所以关于x的不等式ax−bx>c的解集为x>1．
故选：D．  
9.【答案】C 
【解析】解：A选项，等边三角形的内角为60°，360°÷60°=6(个)，所以6个等边三角形可以在一个顶点处实现内角之和等于360°，不符合题意；
B选项，正方形的内角为90°，360°÷90°=4(个)，所以4个正方形可以在一个顶点处实现内角之和等于360°，不符合题意；
C选项，正五边形的内角为108°，360÷108°=313，所以正五边形不能在一个顶点处实现内角之和等于360°，符合题意；
D选项，正六边形的内角为120°，360°÷120°=3(个)，所以3个正六边形可以在一个顶点处实现内角之和等于360°，不符合题意；
故选：C．
正多边形镶嵌有三个条件限制：①边长相等；②顶点公共；③在一个顶点处各正多边形的内角之和为360°.判断一种或几种图形是否能够镶嵌，只要看一看拼在同一顶点处的几个角能否构成周角，若能构成360°，则说明能够进行平面镶嵌，反之则不能．
本题考查了平面镶嵌，掌握平面镶嵌的条件是解题的关键．

10.【答案】A 
【解析】解：取BD中点F，连接EF，
由折叠得∠AED=∠C=90°，ED=CD，
∴∠BED=90°，DE⊥AB，
∴EF=DF=BF=12BD，
∵点D为BC边靠近点C的三等分点，
∴CD=13BC，
∴CD=12BD，
∴ED=CD=EF=DF，
∴△DEF是等边三角形，
∴∠EDF=60°，
∴∠B=30°，
故①正确；
∵∠CDE=180°−∠EDF=120°，
∴∠CDA=∠EDA=12∠CDE=60°，
∴∠CDA=∠EDB，
在△ACD和△BED中，
∠C=∠BEDCD=ED∠CDA=∠EDB，
∴△ACD≌△BED(ASA)，
故②正确；
∴BE=AC，
∵AE=AC，
∴AE=BE，
∴DE垂直平分AB，
故③正确；
∵AE=BE=AC，
∴AB=2AE=2AC，
∴BC= AB2−AC2= (2AC)2−AC2= 3AC，
∴S△ABC=12AC⋅BC=12AC× 3AC= 32AC2≠ 3AC2，
故④错误，
故选：A．
取BD中点F，连接EF，可证明△DEF是等边三角形，则∠EDF=60°，所以∠B=30°，可判断①正确；由∠CDE=120°，得∠CDA=∠EDA=60°，则∠CDA=∠EDB，而∠C=∠BED，CD=ED，即可证明△ACD≌△BED，可判断②正确；由BE=AC，AE=AC，得AE=BE，所以DE垂直平分AB，可判断③正确；由AE=BE=AC，得AB=2AC，则BC= AB2−AC2= 3AC，所以S△ABC=12AC⋅BC= 32AC2≠ 3AC2，可判断④错误，于是得到问题的答案．
此题重点考查直角三角形的两个锐角互余、直角三角形斜边上的中线等于斜边的一半、角平分线的性质、全等三角形的判定与性质、勾股定理等知识，此题综合性强，难度较大．

11.【答案】(x+6)(x−6) 
【解析】
【分析】
此题考查了因式分解−运用公式法，熟练掌握平方差公式是解本题的关键.原式利用平方差公式分解即可．
【解答】
解：原式=(x+6)(x−6)．
故答案为(x+6)(x−6)．
  
12.【答案】45° 
【解析】解：因为任何一个多边形的外角和都是360°，
所以正八边形的每个外角的度数是：360°÷8=45°．
故答案为：45°．
利用多边形的外角和等于360度即可得出答案．
本题主要考查了多边形的外角和定理，熟记任何一个多边形的外角和都是360°是解题的关键．

13.【答案】±2 
【解析】解：根据题意得：x2−4=0且x+1≠0，
解得：x=±2．
故答案是：±2．
根据分式的值为零的条件可以求出x的值．
本题考查了分式的值是0的条件：若分式的值为零，需同时具备两个条件：(1)分子为0；(2)分母不为0.这两个条件缺一不可．

14.【答案】6 
【解析】解：连接PA，过点P分别作AB，AC的垂线段PE，PF，

∵BP，CP是△ABC的角平分线，PD⊥BC，
∴PD=PE=PF=1，
∵△ABC的周长为12，
∴AB+BC+AC=12，
∴S△ABC=S△PAB+S△PBC+S△PAC
=12AB⋅PE+12BC⋅PD+12AC⋅PF
=12(AB+BC+AC)
=12×12
=6，
故答案为：6．
过点P分别作AB，AC的垂线段PE，PF，连接PA，△ABC的面积等于△PAB的面积，△PBC的面积，△PAC的面积和，利用角平分线性质和三角形面积公式将△ABC的面积用△ABC的周长表示出来，即可求出面积．
本题考查角平分线的性质，解题时用到整体思想，能熟练运用整体思想是解题的关键．

15.【答案】−4≤a0①2(x−1)≥3x−1②，
解不等式①，得：x>a，
解不等式②，得：x≤−1，
∵不等式组x−a>02(x−1)≥3x−1恰有3个整数解，
∴这三个整数解为−1，−2，−3，
∴−4≤a4(x+1)①12x−1≤5−32x②，
解不等式①，得：x>2，
解不等式②，得：x≤3，
∴该不等式组的解集为2