


青岛版2.3 轴对称图形习题
展开2023年青岛版数学八年级上册
《2.3 轴对称图形》课时练习

2.誉为全国第三大露天碑林的“浯溪碑林”,摩崖上铭刻着500多方古今名家碑文,其中悬针篆文具有较高的历史意义和研究价值,下面四个悬针篆文文字明显不是轴对称图形的是( )
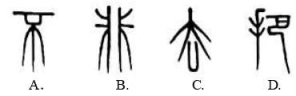
3.甲骨文是中国的一种古代文字,是汉字的早期形式.下列甲骨文中,是轴对称图形的是( )
A.![]() B.
B.![]() C.
C.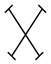 D.
D.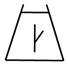
A.线段 B.角 C.等腰三角形 D.正方形
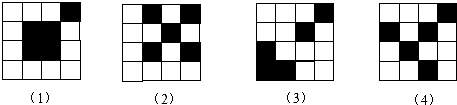
5.如图,把一个正方形对折两次后沿虚线剪下,展开后所得到的图形是( )

6.将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是( )


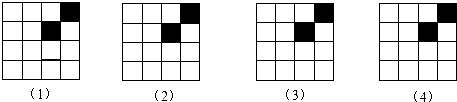
其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
A. 1 B.2 C.3 D.4
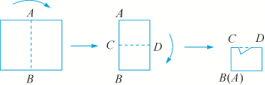
8.如图,将长方形纸片先沿虚线AB按箭头方向向右对折,接着将对折后的纸片沿虚线CD按箭头方向向下对折,然后剪下一个小三角形,再将纸片展开,则展开图是( )
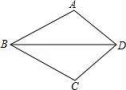
9.如图,四边形ABCD是轴对称图形,BD所在的直线是它的对称轴,AB=3.1cm,CD=2.3cm.则四边形ABCD的周长为 .
10.如图,四边形ABCD沿直线l对折后互相重合,如果AD∥BC,有下列结论:
①AB∥CD;②AB=CD;③AB⊥BC;④AO=OC.
其中正确的结论是 .(把你认为正确的结论的序号都填上)

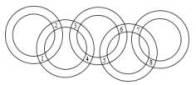
11.国际奥委会会旗上的图案由5个圆环组成.每两个圆环相交的部分叫做曲边四边形,如图所示,从左至右共有8个曲边四边形,分别给它们标上序号.观察图形,我们发现标号为2的曲边四边形(下简称“2”)经过平移能与“6”重合,2还与 成轴对称.(请把能成轴对称的曲边四边形标号都填上)
12.如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有 个.

13.工艺美术中,常需设计对称图案.在如图所示的正方形网格中,点![]() A,D的坐标分别为(1,0),(9,-4).请在图中再找一个格点P,使它与已知的4个格点组成轴对称图形,则点P的坐标为 (如果满足条件的点P不止一个,请将它们的坐标都写出来).
A,D的坐标分别为(1,0),(9,-4).请在图中再找一个格点P,使它与已知的4个格点组成轴对称图形,则点P的坐标为 (如果满足条件的点P不止一个,请将它们的坐标都写出来).

14.如图,△ABC的内部有一点P,且D,E,F是点P分别以AB,BC,AC为对称轴的对称点,则∠ADB+∠BEC+∠CFA= .


16.如图是由16个小正方形组成的正方形网格图,现已将其中的两个涂黑.请你用四种不同的方法分别在下图中再涂黑三个空白的小正方形,使它成为轴对称图形.
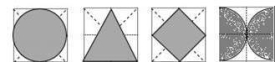
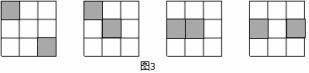
17.用四块如图所示的两色正方形瓷砖,拼成一个新的正方形,使拼成轴对称图案,请至少给出三种不同的拼法:

18.在数学活动课上,王老师要求学生将图1所示的3×3正方形方格纸,剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为要剪掉部分)
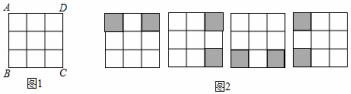
请在图中画出4种不同的设计方案,将每种方案中要剪掉的两个方格涂黑(每个3×3的正方形方格画一种,例图除外)
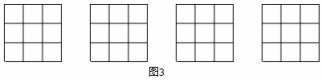
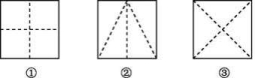
19.将一个正方形按下列要求割成4块:
(1)分割后的整个图形必须是轴对称图形;
(2)所分得的4块图形是全等图形.
请你按照上述两个要求,分别在图①,②,③中的正方形中画出3种不同的分割方法.(不写画法)

 .
.
17.解:根据轴对称要求,设计出利用两色磁砖拼成的正方形如下图所示.

初中数学青岛版八年级上册2.3 轴对称图形课后作业题: 这是一份初中数学青岛版八年级上册2.3 轴对称图形课后作业题,共3页。试卷主要包含了单选题,填空题等内容,欢迎下载使用。
苏科版八年级上册2.3 设计轴对称图案同步测试题: 这是一份苏科版八年级上册2.3 设计轴对称图案同步测试题,共8页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
数学八年级上册2.3 轴对称图形课后练习题: 这是一份数学八年级上册2.3 轴对称图形课后练习题,共12页。试卷主要包含了0分),【答案】D,【答案】A,【答案】B,【答案】C等内容,欢迎下载使用。













