



还剩8页未读,
继续阅读
第一章全等三角形小结-(苏科版) 课件PPT
展开
这是一份第一章全等三角形小结-(苏科版) 课件PPT,共16页。
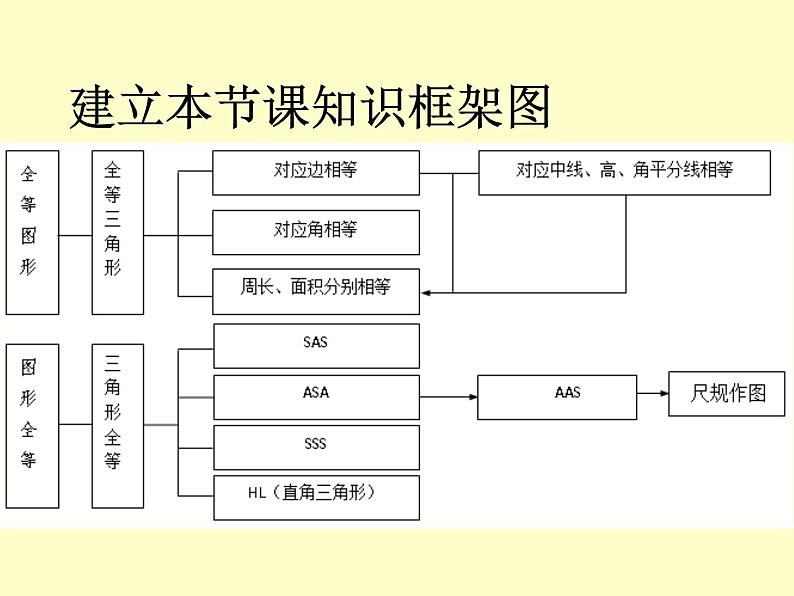
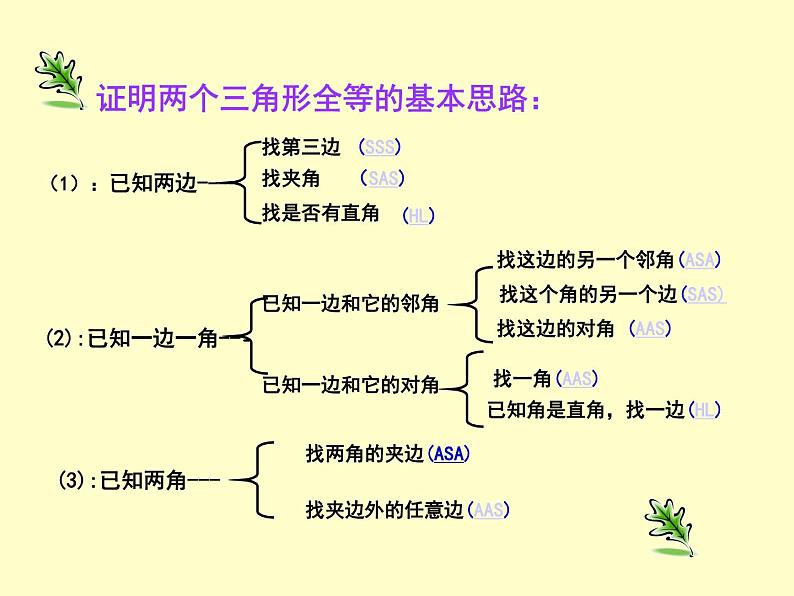
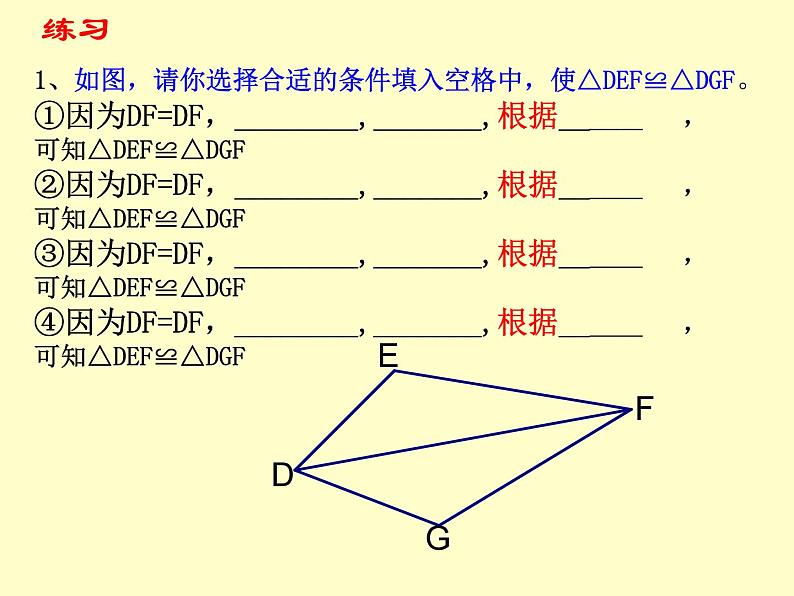
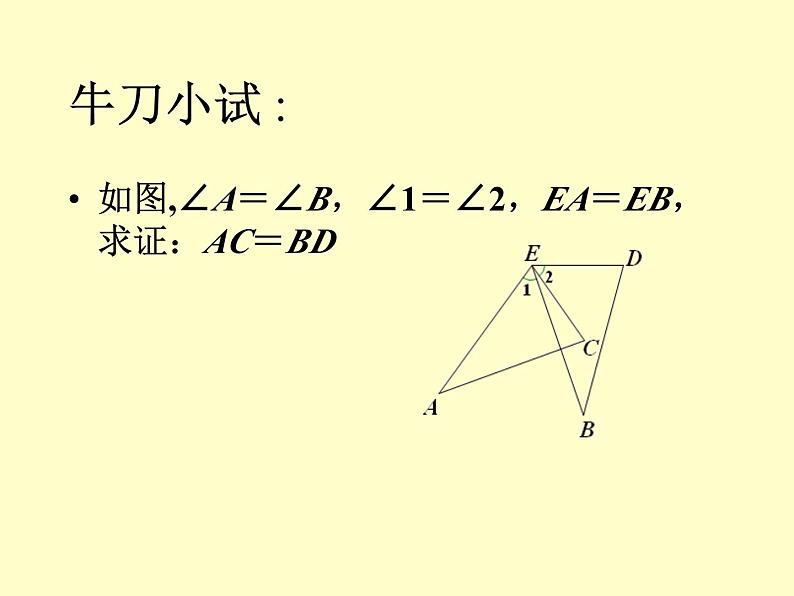
全等三角形复习教学目标:1、使学生熟练掌握全等三角形的判定方法,并能熟练应用。2、通过对图形的剖析,培养学生观察、对图形结构特征识别的能力以及概括综合分析能力,进一步提高学生的推理论证能力。教学重点:全等三角形判定方法的恰当选择与运用。教学难点:图形结构特征的识别与思路分析。建立本节课知识框架图证明两个三角形全等的基本思路:(1):已知两边---- 找第三边(SSS)找夹角(SAS)(2):已知一边一角---已知一边和它的邻角找是否有直角(HL)已知一边和它的对角 找这边的另一个邻角(ASA)找这个角的另一个边(SAS) 找这边的对角 (AAS)找一角(AAS)已知角是直角,找一边(HL)(3):已知两角---找两角的夹边(ASA)找夹边外的任意边(AAS)1、如图,请你选择合适的条件填入空格中,使△DEF≌△DGF。 ①因为DF=DF,________,_______,根据______ ,可知△DEF≌△DGF②因为DF=DF,________,_______,根据______ ,可知△DEF≌△DGF③因为DF=DF,________,_______,根据______ ,可知△DEF≌△DGF④因为DF=DF,________,_______,根据______ ,可知△DEF≌△DGF练习例题教学: 例:已知:如图,AB、CD相交于点E, 且E是AB、CD 的中点. 求证:AC∥DB.变式: 如图,点C、F在AD上,且AF=DC,∠B=∠E,∠A=∠D, 你能证明AB=DE吗?如图,∠A=∠B,∠1=∠2,EA=EB,求证:AC=BD牛刀小试 :2、如图,在△ABC 中,AD⊥ BC,CE⊥ AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件: ,使△AEH≌△CEB。3、已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2,图中全等的三角形共有( )A.1对 B.2对 C.3对 D.4对 D数学好玩●试探索AD、BE、DE的大小关系例2如图,A,B,C三点在同一直线上,分别以AB,BC为边在AC同侧作等边⊿ABD和等边⊿BCE,AE交BD于点F,DC交BE于点G,(1) AE与DC相等吗? (2)BF与BG相等吗? .好美的图形课堂练习1、如图1,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC。若∠B=200,CD=5cm,则∠C=______,BE=_______.2、如图2,若OB=OD,∠A=∠C,若AB=3cm,则CD=______ 3. 测量如图河的宽度,某人在河的对岸找到一参照物树木A, 视线 AB与河岸垂直,然后该人沿河岸步行10步(每步约0.75M)到O处,进行标记,再向前步行10步到D处,最后背对河岸向前步行20步,此时树木A,标记O,恰好在同一视线上,则河的宽度为 米。15ABODC思考题 如图,E,D是⊿ABC中BC边上的两点,AD=AE,要证明⊿ABE≌⊿ACD,还应该补充一个什么条件。BDECA解:(1)BE=CD (2) BD=CE (3)AB=AC(7)S⊿ABE=S⊿ACD (8)S⊿ABD=S⊿ACD (9)⊿ABD≌⊿ACE (4)∠B= ∠ C (5)∠BAE=∠CAD(6)∠BAD=∠CAE 教学反思●通过本节课的学习,你有哪些收获?
全等三角形复习教学目标:1、使学生熟练掌握全等三角形的判定方法,并能熟练应用。2、通过对图形的剖析,培养学生观察、对图形结构特征识别的能力以及概括综合分析能力,进一步提高学生的推理论证能力。教学重点:全等三角形判定方法的恰当选择与运用。教学难点:图形结构特征的识别与思路分析。建立本节课知识框架图证明两个三角形全等的基本思路:(1):已知两边---- 找第三边(SSS)找夹角(SAS)(2):已知一边一角---已知一边和它的邻角找是否有直角(HL)已知一边和它的对角 找这边的另一个邻角(ASA)找这个角的另一个边(SAS) 找这边的对角 (AAS)找一角(AAS)已知角是直角,找一边(HL)(3):已知两角---找两角的夹边(ASA)找夹边外的任意边(AAS)1、如图,请你选择合适的条件填入空格中,使△DEF≌△DGF。 ①因为DF=DF,________,_______,根据______ ,可知△DEF≌△DGF②因为DF=DF,________,_______,根据______ ,可知△DEF≌△DGF③因为DF=DF,________,_______,根据______ ,可知△DEF≌△DGF④因为DF=DF,________,_______,根据______ ,可知△DEF≌△DGF练习例题教学: 例:已知:如图,AB、CD相交于点E, 且E是AB、CD 的中点. 求证:AC∥DB.变式: 如图,点C、F在AD上,且AF=DC,∠B=∠E,∠A=∠D, 你能证明AB=DE吗?如图,∠A=∠B,∠1=∠2,EA=EB,求证:AC=BD牛刀小试 :2、如图,在△ABC 中,AD⊥ BC,CE⊥ AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件: ,使△AEH≌△CEB。3、已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2,图中全等的三角形共有( )A.1对 B.2对 C.3对 D.4对 D数学好玩●试探索AD、BE、DE的大小关系例2如图,A,B,C三点在同一直线上,分别以AB,BC为边在AC同侧作等边⊿ABD和等边⊿BCE,AE交BD于点F,DC交BE于点G,(1) AE与DC相等吗? (2)BF与BG相等吗? .好美的图形课堂练习1、如图1,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC。若∠B=200,CD=5cm,则∠C=______,BE=_______.2、如图2,若OB=OD,∠A=∠C,若AB=3cm,则CD=______ 3. 测量如图河的宽度,某人在河的对岸找到一参照物树木A, 视线 AB与河岸垂直,然后该人沿河岸步行10步(每步约0.75M)到O处,进行标记,再向前步行10步到D处,最后背对河岸向前步行20步,此时树木A,标记O,恰好在同一视线上,则河的宽度为 米。15ABODC思考题 如图,E,D是⊿ABC中BC边上的两点,AD=AE,要证明⊿ABE≌⊿ACD,还应该补充一个什么条件。BDECA解:(1)BE=CD (2) BD=CE (3)AB=AC(7)S⊿ABE=S⊿ACD (8)S⊿ABD=S⊿ACD (9)⊿ABD≌⊿ACE (4)∠B= ∠ C (5)∠BAE=∠CAD(6)∠BAD=∠CAE 教学反思●通过本节课的学习,你有哪些收获?
相关资料
更多









