第一章全等三角形小结-(苏科版) 课件PPT

这是一份第一章全等三角形小结-(苏科版) 课件PPT，共17页。

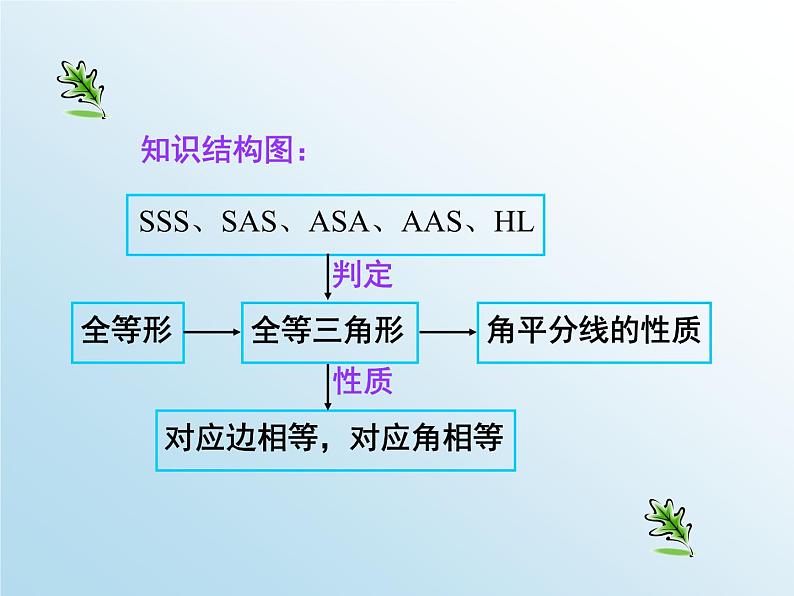
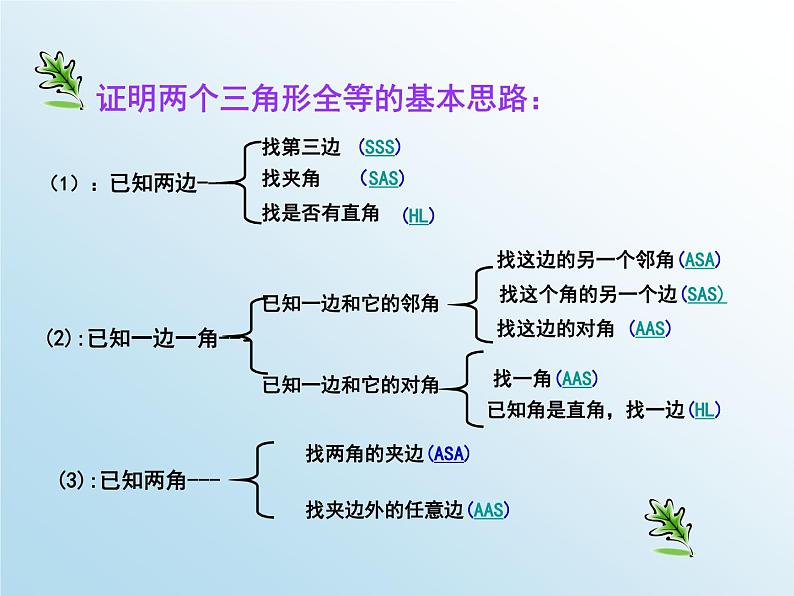
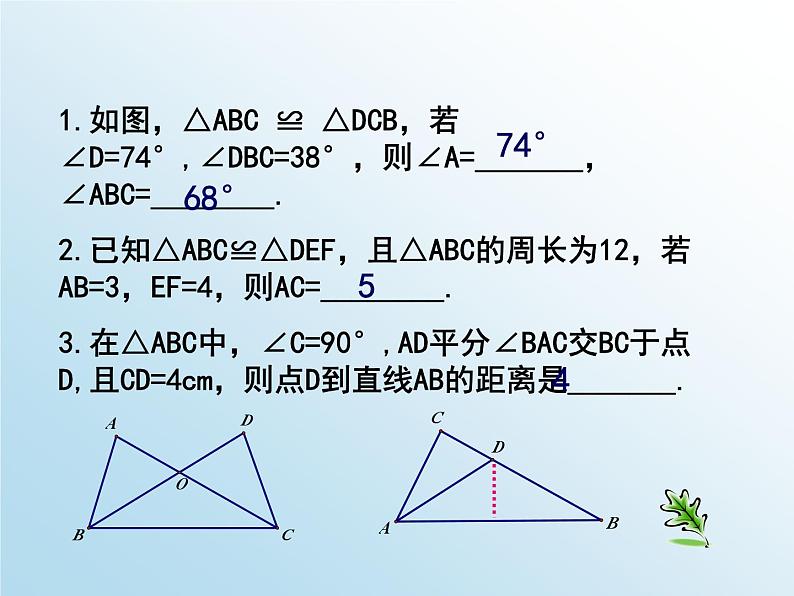
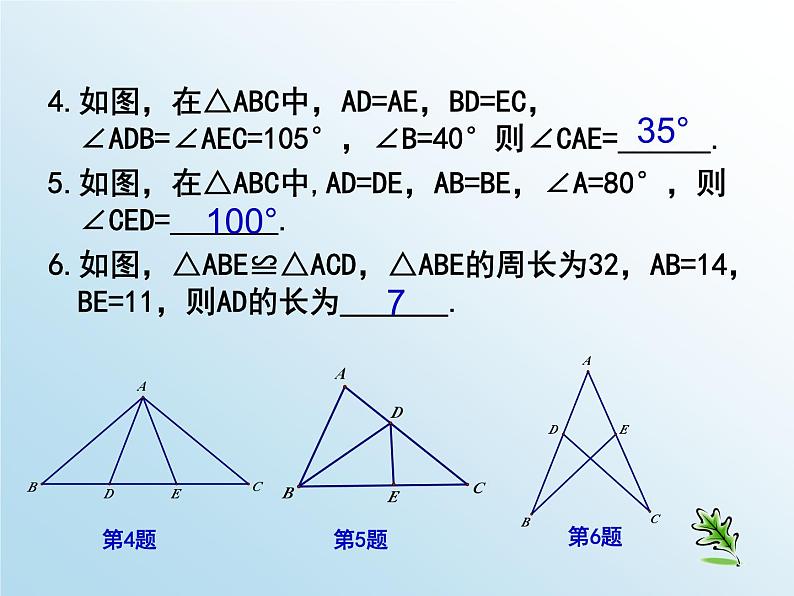
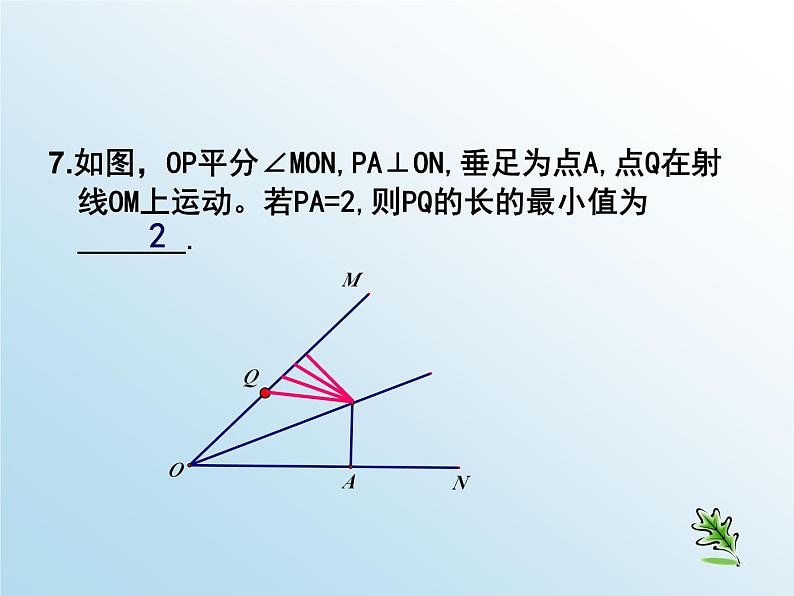
同学们,当老师提问或请同学们练习时，你可以按播放器上的暂停键思考或练习，然后再点击播放键.八年级寒假作业导学微课P19-20课题 单 位：句容市华阳中学 主 讲：邱苗苗 一 归纳梳理二 题目分析本讲结构 　 知识结构图：证明两个三角形全等的基本思路：（1）：已知两边---- 找第三边(SSS)找夹角（SAS)(2):已知一边一角---已知一边和它的邻角找是否有直角(HL)已知一边和它的对角 找这边的另一个邻角(ASA)找这个角的另一个边(SAS) 找这边的对角 (AAS)找一角(AAS)已知角是直角，找一边(HL)(3):已知两角---找两角的夹边(ASA)找夹边外的任意边(AAS)1.如图，△ABC ≌ △DCB，若∠D=74°,∠DBC=38°，则∠A=_______，∠ABC=________.2.已知△ABC≌△DEF，且△ABC的周长为12，若AB=3，EF=4，则AC=________.3.在△ABC中，∠C=90°,AD平分∠BAC交BC于点D,且CD=4cm，则点D到直线AB的距离是_______.74°68°544.如图，在△ABC中，AD=AE，BD=EC，∠ADB=∠AEC=105°，∠B=40°则∠CAE=______.5.如图，在△ABC中,AD=DE，AB=BE，∠A=80°，则∠CED=_______.6.如图，△ABE≌△ACD，△ABE的周长为32，AB=14，BE=11，则AD的长为_______.第4题第6题第5题35°100°77.如图，OP平分∠MON,PA⊥ON,垂足为点A,点Q在射线OM上运动。若PA=2,则PQ的长的最小值为_______.2二、选择题8.两个全等图形中可以不同的是（ ） A.位置 B.形状 C.对应角的度数 D.面积9.△ABC中，∠B=∠C,与△ABC全等的三角形有一个角是100°，那么△ABC中与这角对应相等的角是（ ） A. ∠A B.∠B C.∠C D.∠B或∠C10.△ABC是不等边三角形，DE=BC,以D.E为两个顶点作位置不同的三角形，使所作的三角形与△ABC全等，这样的三角形最多可以画出（ ） A. 2个 B.4个 C.6个 D.8个11.在△ABC和△DEF中，∠B=∠E,∠C=∠F.在下列条件中，增加以后能证明△ABC≌△DEF的是（ ） A. AB=DF B.BC=DF C.BC=EF D.AC=DEACBA12. 如图，△ABC≌△DEF,∠A=85°，∠B=60°,AB=8,EH=2.求∠F的度数和DH的长13.如图，AB∥DE,BC∥EF,点D.C在AF上，且AD=CF，求证△ABC≌△DEF.∵△ABC≌△DEF∴∠F=∠ACB=180°-∠A-∠B=35°∴DH=DE-EH=AB-EH=6∵AB∥DE∴∠A=∠EDC∵BC∥EF∴∠BCA=∠F∵AD=CF∴CA=DF在△ABC和△DEF中∠A=∠EDCCA=DF∠BCA=∠F∴△ABC ≌△ DEF（ASA）14.如图,在△PAB中，点C.D在边AB上，PC=PD, 请你添加一个条件，使图中存在全等三角形，并说明理由。所添条件为 ， 你得到的一对全等三角形是 ，请证明。(AC=BD)(∠APC=∠BPD）)(∠A=∠B) AD=BC△APC ≌△ BPD△PAD ≌△ PBC(AP=BP)∠PCD=∠PDC, PC=PD∠PCD=∠PDCAD=BC∴△PAD ≌△ PBC (SAS）．△APC ≌△ BPD15.如图,每个小正方形的边长都为1个单位长度。（1）你能用全等三角形的知识来说明AB=AC吗？（2）试猜想，AB,AC有怎样的位置关系？是说明你的理由。ABCDEAD＝BE∴△ADC ≌△ BEA（SAS）．在△ADC和△BEA中CD＝AE∠CDA＝∠AEB∴AC=AB∠C＝∠BAE∵∠C+∠DAC=90°∴∠BAE+∠DAC=90°∴∠CAB=90°∴AB⊥AC16（1）如图1，AB=CD,AD=BC,O为AC中点，过点O的直线分别与AD、BC相交于M、N，那么MO与NO有什么关系？请说明理由。（2）若过点O的直线旋转至图2的情况，其余条件你变，那么图1中的MO与NO的关系成立么？请说明理由。AB＝CDAD＝CB∴△ABC ≌△ CAD（SSS）．∵O为AC中点∴AO=CO在△ABC和△CDA中AC＝CA∴△AMO≌△ CNO（ASA）．∴∠CAD＝∠BCA在△AMO和△CNO中∠CAD＝∠BCAAO=CO∠MOA＝∠NOC∴MO=NO 一路下来，我们共同回顾了所学知识，又利用这些知识解决了寒假作业中的一些问题，相信你一定有所收获。结束语谢谢本节寒假作业解答释疑结束