第一章全等三角形小结-(苏科版)课件PPT

这是一份第一章全等三角形小结-(苏科版)课件PPT，共35页。

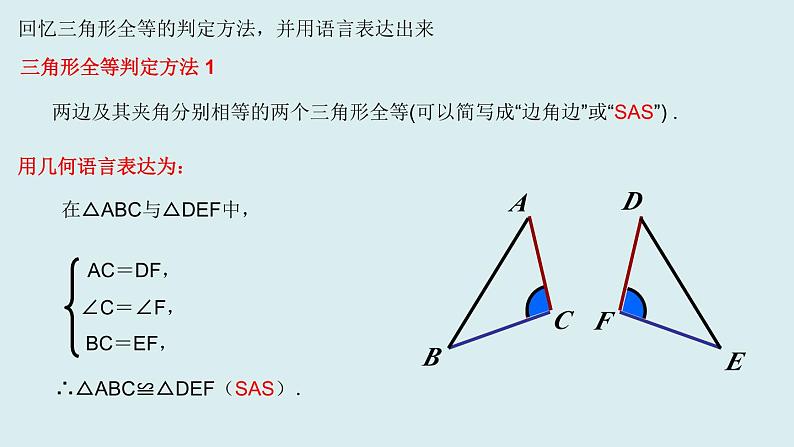
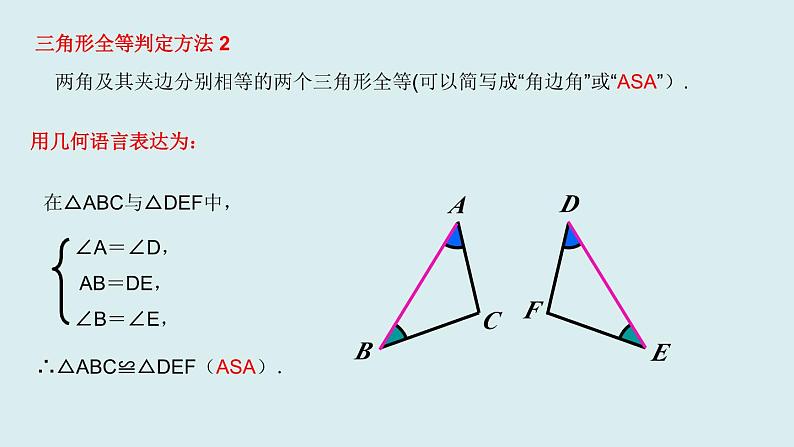
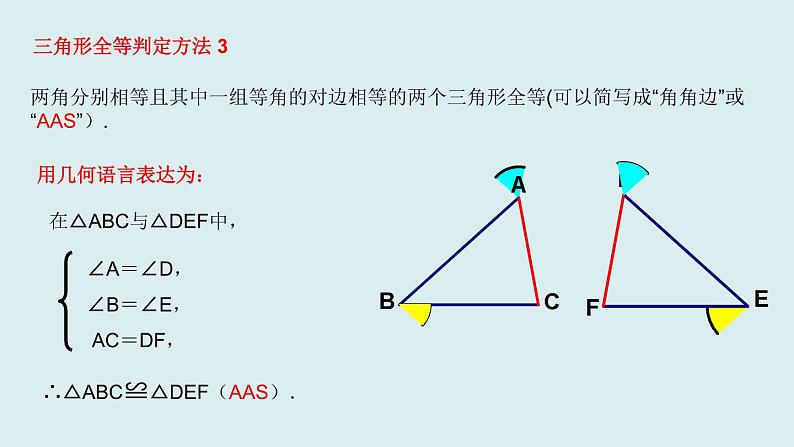
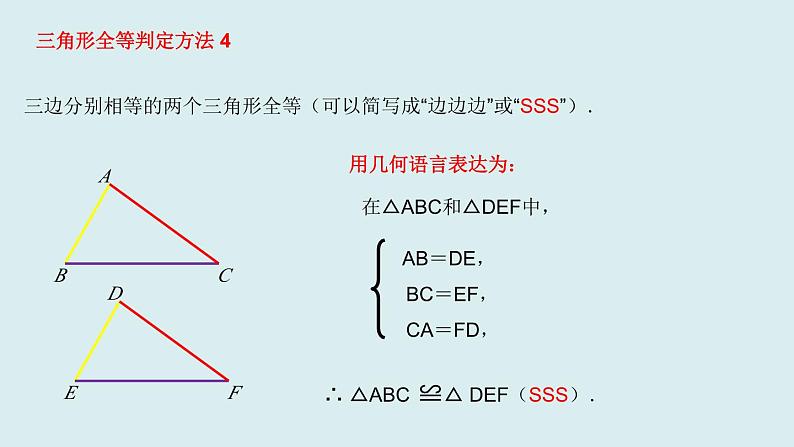
2021八年级上册 数学全等三角形的复习（1）两个能够完全重合的三角形叫全等三角形。（2）全等三角形的对应角相等，对应边相等。（3）判定两个三角形全等的公理或定理：①一般三角形有SAS、ASA、AAS、SSS 。②直角三角形有SAS、ASA、AAS、SSS 、 HL（千万不要将SSA条件作为SAS条件来用）。 如何分析相关题目1、证明两个三角形全等，要结合题目的条件和结论，选择恰当的判定方法2、全等三角形，是证明两条线段或两个角相等的重要方法之一，证明时 　①要观察待证的线段或角，在哪两个可能全等的三角形中。 　②分析要证两个三角形全等，已有什么条件，还缺什么条件。 　③有公共边的，公共边一定是对应边；有公共角的，公共角一定是对应角；有对顶角，对顶角也是对应角。总之，证明过程中能用简单方法的就不要绕弯路。 三角形全等判定方法 1用几何语言表达为：在△ABC与△DEF中，∴△ABC≌△DEF（SAS）． 两边及其夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”) .FEDCBA回忆三角形全等的判定方法，并用语言表达出来FEDCBA 三角形全等判定方法 2在△ABC与△DEF中，用几何语言表达为：∴△ABC≌△DEF（ASA）．　两角及其夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”）.∠A＝∠D， AB＝DE，∠B＝∠E， 三角形全等判定方法 3在△ABC与△DEF中，用几何语言表达为：∴△ABC≌△DEF（AAS）．两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”）.∠A＝∠D，∠B＝∠E， AC＝DF，三边分别相等的两个三角形全等（可以简写成“边边边”或“SSS”）．在△ABC和△DEF中， AB＝DE， BC＝EF， CA＝FD，∴ △ABC ≌△ DEF（SSS）．三角形全等判定方法 4用几何语言表达为：用几何语言表达为：斜边和一条直角边分别相等的两个直角三角形全等.（简写为：“斜边、直角边”或“HL”）．三角形全等判定方法 51.如图（1），点D在AB上，点E在AC上，CD与BE相交于点O，且AD=AE,AB=AC.若∠B=20°,CD=5cm，则∠C= ,BE= .说说理由.3.如图（3），若OB=OD，∠A=∠C，若AB=3cm，则CD= . 说说理由. 20°5cm3cm挖掘“隐含条件”5.如图（5），AC=BD，AD=BC，试说明∠C=∠D的理由图（4）归纳点拨：公共边，公共角，对顶角这些都是隐含的边，角相等的条件！解题时要善于发现并利用。1.（嘉兴中考)如图，在△ABC与△DCB中，AC与BD交于点E，且∠A=∠D，AB=DC.(1)求证：△ABE≌△DCE.(2)当∠AEB=50°时，求∠EBC的度数.直击中考 2.(大庆中考)如图，把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°，使得点C旋转到AB边上的一点D，点A旋转到点E的位置.F，G分别是BD，BE上的点，BF=BG，延长CF与DG交于点H.(1)求证：CF=DG.(2)求出∠FHG的度数. 3.如图所示，AB＝DC，AD＝BC，DE＝BF. 求证：BE＝DF. ［解析］ BE和DF分别在△ABE与△CDF（或△BDE与△DBF）中，由已知条件不能直接推导它们全等，结合图形，连接BD，可证△ABD≌△CDB，得∠A＝∠C，再去证△ABE≌△CDF.4.(泉州中考)如图，已知AD是△ABC的中线，分别过点B，C作BE⊥AD于点E，CF⊥AD交AD的延长线于点F.求证：D是EF的中点。【课堂小结】一、寻找对应元素的方法1.全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边.2.全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角.3.有公共边的，公共边常是对应边.4.有公共角的，公共角常是对应角.5.有对顶角的，对顶角常是对应角.6.两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角)，一对最短边(或最小角)是对应边(或对应角).二、应用全等三角形解题思路1.利用全等三角形证明线段相等时，要找好背景三角形.2.求证线段或角相等时考虑转化为证明它们所在的三角形全等.3.当一个图形的某些条件变化后，要能分清变与不变的结果.4.当遇到多边形问题时一般转化为三角形的问题解决.1.如图，已知∠B＝∠D，AB＝DE，要△ABC≌△DEC；则需添加的条件_________.2.如图，在△ABC和△ABD中，∠C=∠D=90°，使△ABC≌△ABD，则需要加条件 .归纳点拨：添加条件的题目.首先要找到已具备的条件,这些条件有些是题目已知条件 ,有些是图中隐含条件.然后根据已知条件选择符合判定定理的相应的的条件.开放训练两边和其中一边的对角对应相等的两个三角形不一定全等做这类题目有一个易错点：1.如图，AE=CF，∠AFD=∠CEB，DF=BE，△AFD与△ CEB全等吗？为什么？BDBCEF2.如图（5）∠CAE=∠BAD，∠B=∠D，AC=AE，△ABC与△ADE全等吗？为什么？点拨：处理这类问题，应先找出直接条件，再把间接条件利用线段的和差，角的和差关系转化成直接条件。然后判断出符合哪一个判定定理。AAECD1.(湘潭中考)如图，在△ABC中，AB=AC，点D，E在BC上，连接AD，AE.如果只添加一个条件使∠DAB=∠EAC，则添加的条件不能为　(　　)A.BD=CE B.AD=AE C.DA=DE D.BE=CD2.(昭通中考)如图，AF=DC，BC∥EF，只需补充一个条件　　　　　　　　　　　，就得△ABC≌△DEF.3.(珠海中考)如图，在△ABC中，AB=AC，AD是高，AM是△ABC外角∠CAE的平分线.(1)用尺规作图方法，作∠ADC的平分线DN.(保留作图痕迹，不写作法和证明)(2)设DN与AM交于点F，判断△ADF的形状(只写结果).本章总结提升4.一位经历过战争的老人讲述了这样一个故事：在一次战役中，我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡，需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下，一个战士想出来这样一个办法：他面向碉堡的方向站好，然后调整帽子，使视线通过帽檐正好落在碉堡的底部；然后，他转过一个角度，保持刚才的姿态，这时视线落在了自己所在岸的某一点上；接着，他用步测的方法量出自己与那个点的距离，这个距离就是他与碉堡间的距离.请解释其中的道理.本章总结提升 小明的设计方案：先在池塘旁取一个能直接到达A和B处的点C，连结AC并延长至D点，使AC=DC，连结BC并延长至E点，使BC=EC，连结CD，用米尺测出DE的长，这个长度就等于A，B两点的距离。请你说明理由。 AC=DC  ∠ACB=∠DCE BC=EC △ACB≌△DCE(SAS) AB=DEECBAD5、如图线段AB是一个池塘的长度，现在想测量这个池塘的长度，在水上测量不方便，你有什么好的方法较方便地把池塘的长度测量出来吗？想想看。解：在△ACB和△DCE中，（全等三角形对应边相等。）．八（9）班同学到野外上数学活动课，为测量池塘两端A、B的距离，设计如下方案：（Ⅰ）如图1，先在平地上取一个可直接到达A、B的点C，连接AC、BC，并分别延长AC至D，BC至E，使DC＝AC，EC＝BC，最后测出DE的距离即为AB的长；（Ⅱ）如图2，先过B点作AB的垂线BF，再在BF上取C、D两点使BC＝CD，接着过D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离. 阅读后回答下列问题：（1）方案（Ⅰ）是否可行？请说明理由。（2）方案（Ⅱ）是否可行？请说明理由。 （3）方案（Ⅱ）中作BF⊥AB，ED⊥BF的目的是 ；若条件改为满足∠ABD＝∠BDE≠90°，方案（Ⅱ）是否成立？开放训练通过这节课的学习你有什么收获?知道应用如何应用全等三角形判定方法判定三角形全等全等三角形探索角等.线段等.平行全等三角形在生活中有广泛的应用 　这节课你有什么收获，还有什么疑惑？与你的同伴进行交流.　　　　通过这节课的学习你有什么收获?作业：书本第32页第17、18题谢谢！