第一章全等三角形小结-(苏科版) 课件PPT

这是一份第一章全等三角形小结-(苏科版) 课件PPT，共15页。

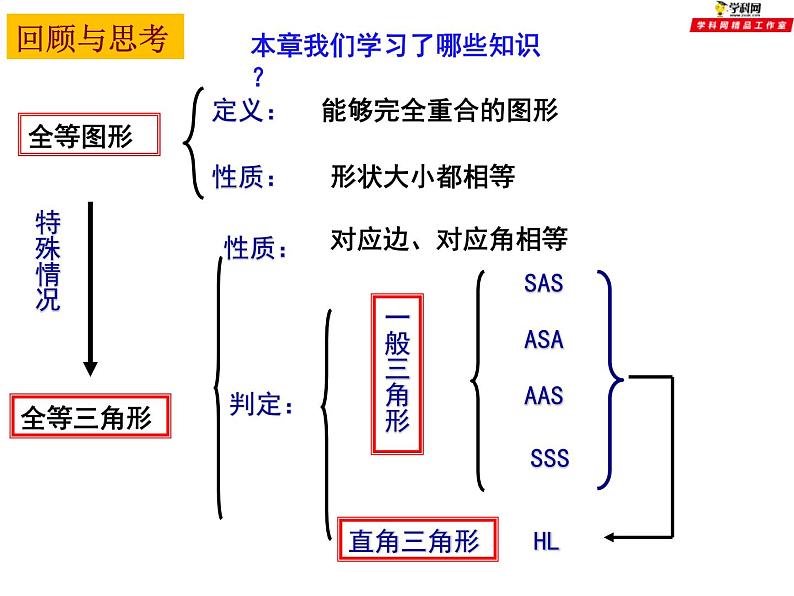
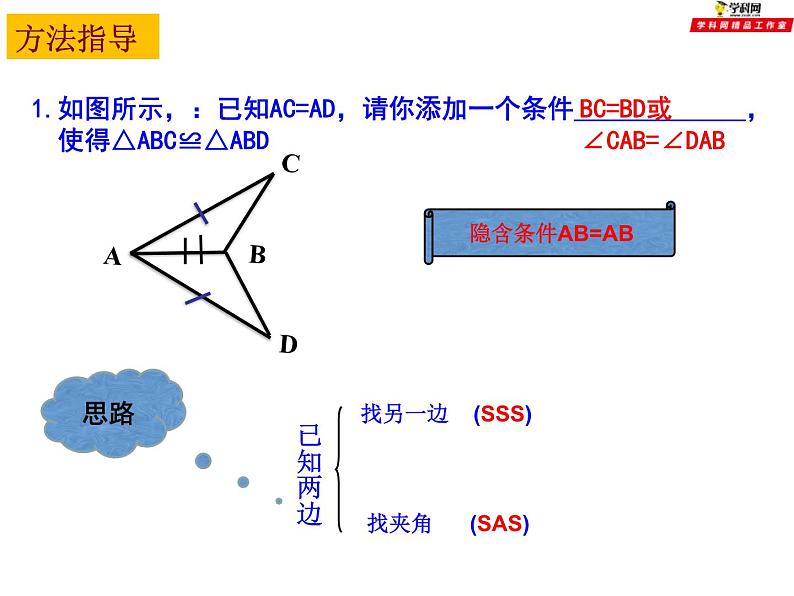
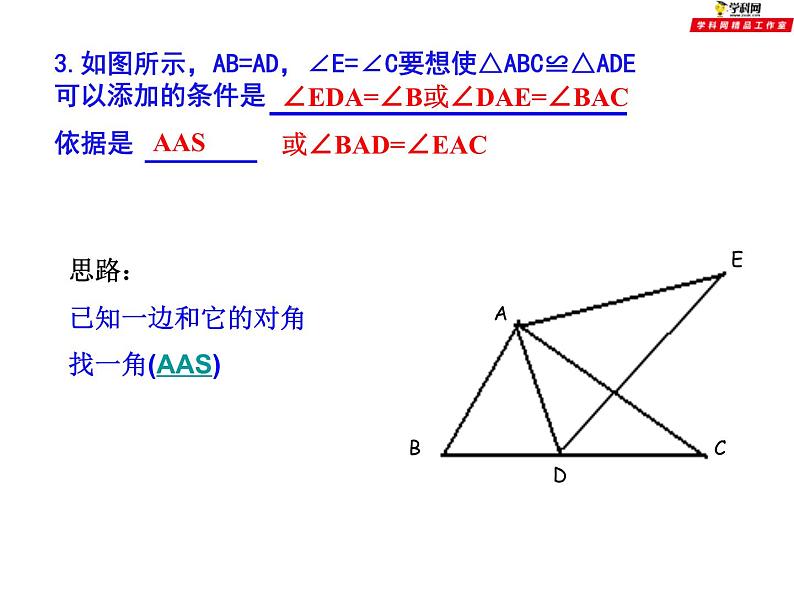
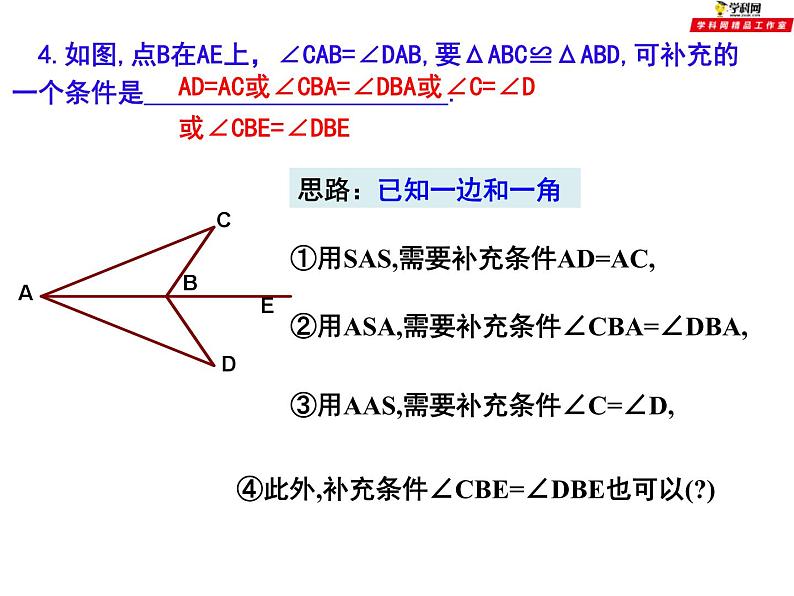
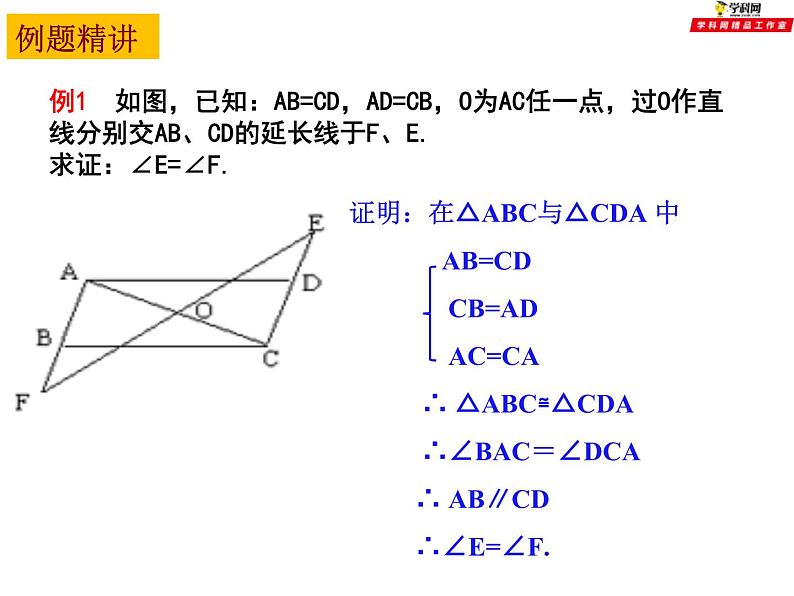
《全等三角形》 小结与思考（1）全等三角形能够完全重合的图形形状大小都相等对应边、对应角相等SASASAAASSSSHL回顾与思考本章我们学习了哪些知识？1.如图所示，：已知AC=AD，请你添加一个条件 ， 使得△ABC≌△ABD隐含条件AB=AB方法指导思路BC=BD或∠CAB=∠DAB 2.如图所示：已知∠B=∠C，请你添加一个条件 ， 使得△ABE≌△ACD∠A为公共角思路AB=AC或AE=AD或BE=CD思路：已知一边和它的对角找一角(AAS)∠EDA=∠B或∠DAE=∠BAC或∠BAD=∠EAC AAS 4.如图,点B在AE上，∠CAB=∠DAB,要ΔABC≌ΔABD,可补充的一个条件是 .AD=AC或∠CBA=∠DBA或∠C=∠D或∠CBE=∠DBE ①用SAS,需要补充条件AD=AC, ②用ASA,需要补充条件∠CBA=∠DBA, ③用AAS,需要补充条件∠C=∠D, ④此外,补充条件∠CBE=∠DBE也可以(?) 思路：已知一边和一角例题精讲例1 如图，已知：AB=CD，AD=CB，O为AC任一点，过O作直线分别交AB、CD的延长线于F、E.求证：∠E=∠F.例2 如图. ∠ ACB=90°，AC=BC，BE ⊥ CE，AD⊥ CE，垂足分别为E，D，图中有哪条线段与AD相等，并说明理由。解：AD=CE.∵BE ⊥CE，AD ⊥CE，∴∠ BEC= ∠ CDA= 90°,又∵∠ACB=90°，即∠ BCE+ ∠ ACE=90°,∠ DAC+ ∠ ACD=90°∴∠ BCE= ∠ DAC， 又∵AC=BC根据AAS，可以知道△BEC≌△CDA所以AD=CE 例3 如图，在△ABC中，AD为BC边上的中线，试说明AB＋AC 与2AD之间的大小关系。小结：对于三角形的中线，我们可以通过延长中线的1倍，来构造全等三角形。EDBAC1.已知△ABC和△DEF,下列条件中,不能保证△ABC和△DEF全等的是( )A.AB=DE,AC=DF,BC=EF B. ∠A= ∠ D, ∠ B= ∠ E,AC=DFC.AB=DE,AC=DF, ∠A= ∠D D.AB=DE,BC=EF, ∠ C= ∠ FD课堂练习2、已知：如图，CD⊥AB，BE⊥AC，垂足分别为D、E，BE、CD相交于O点，∠1=∠2，图中全等的三角形共有( )A．1对 B．2对 C．3对 D．4对 D3、如图，△ABC中，AD⊥BC，垂足为D，BE⊥AC，垂足为E，AD、BE相交于点F。如果BF＝AC，那么∠ABC的度数是 （　 ）A、400　 B、 450　 C、 500　 D、600B5.如图，△ABC≌△AED，∠C＝400，∠EAC＝300，∠B＝300，则∠D＝＿＿＿＿＿＿＿∠EAD＝＿＿＿＿＿40011006.如图，∠A＝∠B，∠1＝∠2，AD＝BC，则全等的三角形是＿＿＿＿＿＿＿＿＿△AFC≌△BED7.已知如图，∠3＝∠4，要说明△ABC≌△DCB（1）若以“SAS”为依据，则需添加一个条件＿＿＿＿＿＿（2）若以“AAS”为依据，则需添加一个条件＿＿＿＿＿＿（3）若以“ASA”为依据，则需添加一个条件＿＿＿＿＿＿AC＝BD∠BAC＝∠CDB∠1＝∠2 8.已知,如图,E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF ⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点,（1）求证：MB=MD，ME=MFBFEACDEFMABCDM（2）当E、F两点移到移到至如图所示的位置时，其它条件不变，上述结论能否成立？若成立，请说明你的理由。 已知：如图，DE⊥AB于E，DF⊥AC于F,若BD=CD、BE=CF，试写出AB+AC与AE之间的等量关系，并证明.拓展延伸课堂小结学习全等三角形应注意以下几个问题：（1）要正确区分“对应边”与“对边”，“对应角”与“对角”的不同含义；（2）表示两个三角形全等时，表示对应顶点的字母要写在对应的位置上；（3）要记住“有三个角分别相等”或“有两边及其中一边的对角分别相等”的两个三角形不一定全等；（4）时刻注意图形中的隐含条件，如 “公共角” 、“公共边”、“对顶角”。谈谈这一节课你有哪些收获？