第12章证明复习课件-（苏教科）

这是一份第12章证明复习课件-（苏教科），共14页。
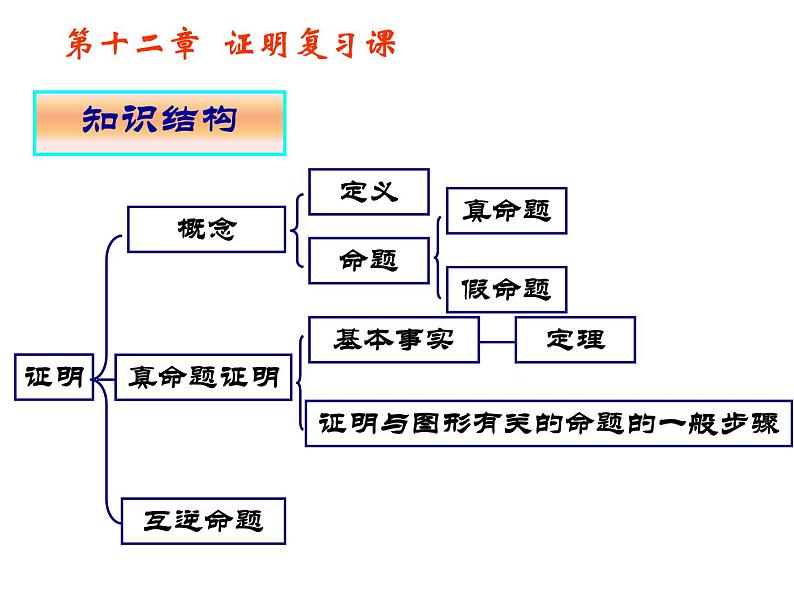
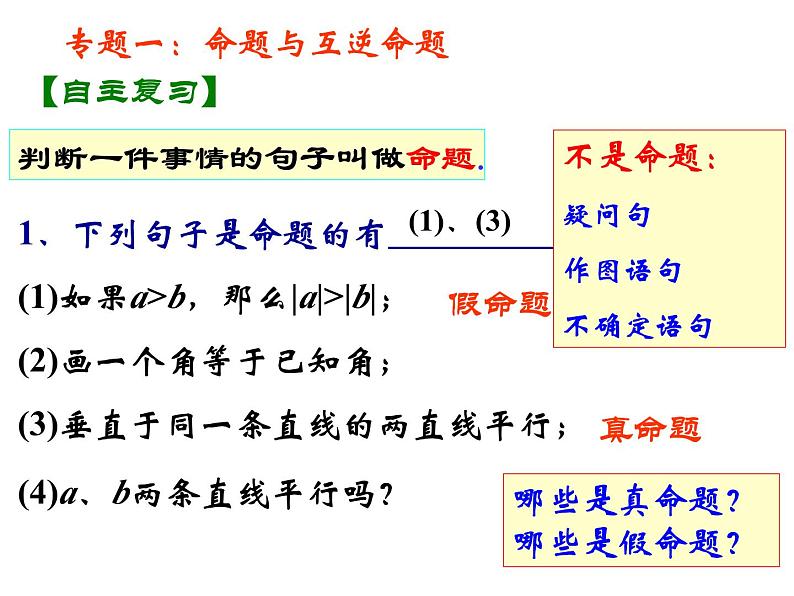
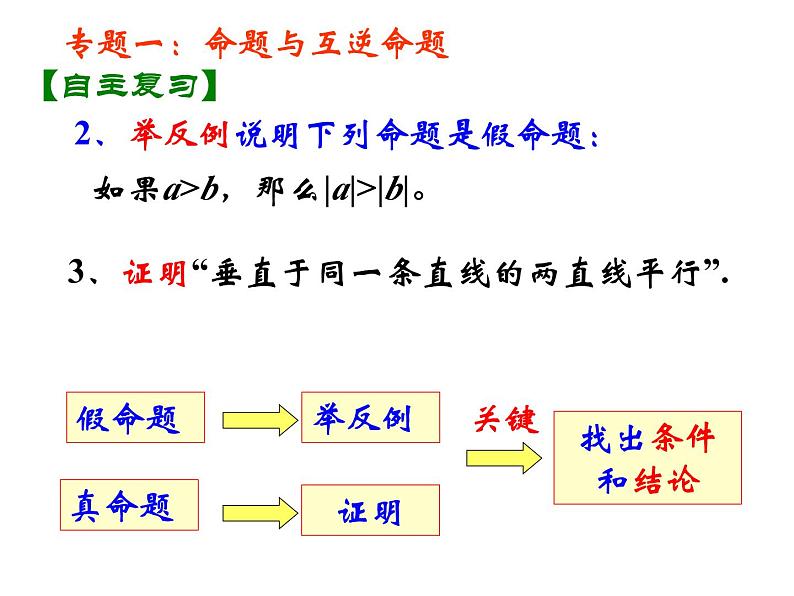
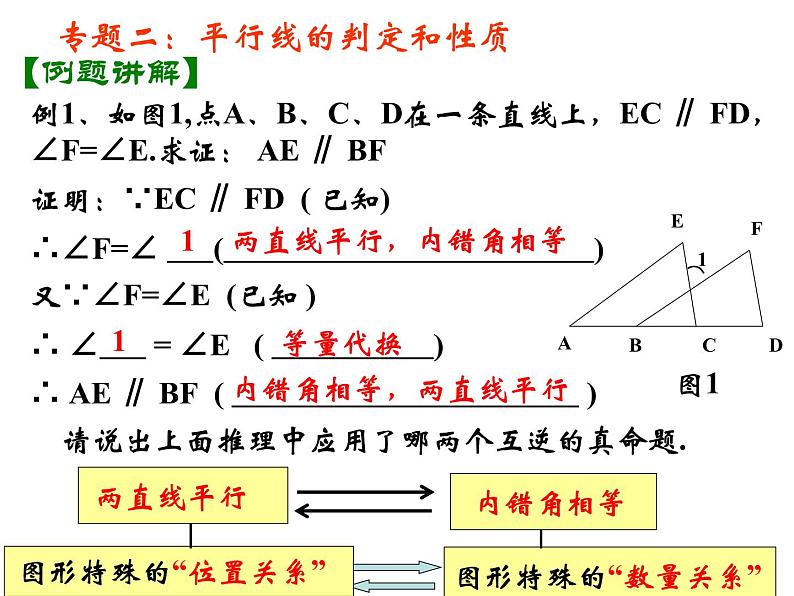
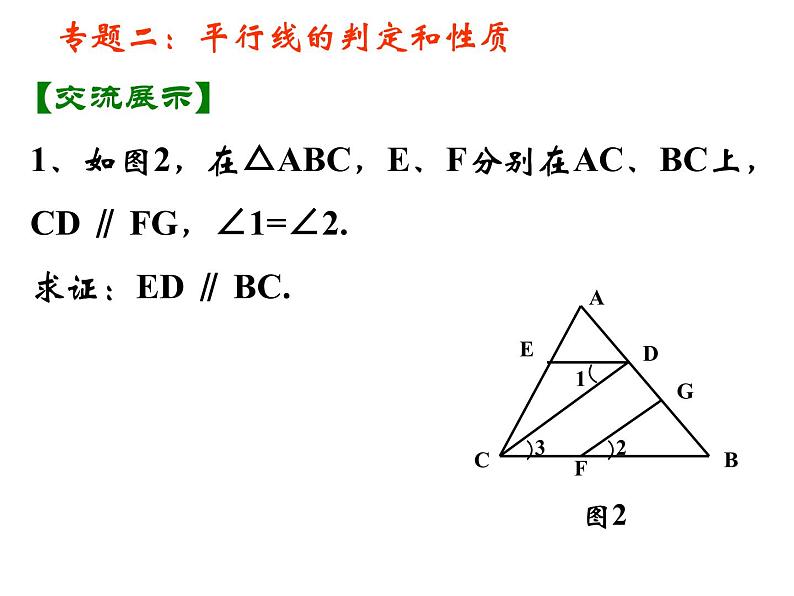
第十二章　证明 七年级(下册)初中数学证明概念真命题证明互逆命题定义命题真命题假命题基本事实定理证明与图形有关的命题的一般步骤知识结构第十二章 证明复习课判断一件事情的句子叫做命题.1、下列句子是命题的有 .(1)如果a>b，那么|a|>|b|；(2)画一个角等于已知角；(3)垂直于同一条直线的两直线平行；不是命题：疑问句作图语句不确定语句哪些是真命题？哪些是假命题？专题一：命题与互逆命题【自主复习】(1)、(3)(4)a、b两条直线平行吗？假命题真命题2、举反例说明下列命题是假命题： 如果a>b，那么|a|>|b|。假命题真命题举反例证明找出条件和结论关键专题一：命题与互逆命题【自主复习】3、证明“垂直于同一条直线的两直线平行”.4.指出下列命题的条件和结论，并说出其逆命题.(1)如果a>b，那么|a|>|b|.逆命题:如果|a|>|b| ，那么a>b.(2) 垂直于同一条直线的两条直线平行.条件:垂直于同一条直线的两条直线.结论:这两条直线平行. 逆命题:如果两条直线平行，那么这两条直线垂直于同一条直线.专题一：命题与互逆命题【自主复习】简写：互相平行的两直线 垂直于同一条直线.条件: a>b.结论: |a|>|b.例1、如图1,点A、B、C、D在一条直线上，EC ∥ FD，∠F=∠E.求证： AE ∥ BF证明：∵EC ∥ FD ( 已知)∴∠F=∠ ( )又∵∠F=∠E (已知 )∴ ∠ = ∠E ( )∴ AE ∥ BF ( )请说出上面推理中应用了哪两个互逆的真命题.1两直线平行，内错角相等1等量代换内错角相等，两直线平行【例题讲解】图1专题二：平行线的判定和性质专题二：平行线的判定和性质1、如图2，在△ABC，E、F分别在AC、BC上，CD ∥ FG，∠1=∠2.求证：ED ∥ BC.【交流展示】专题二：平行线的判定和性质 如图3，在△ABC，点E、点F分别在AC、BC上，CD⊥AB于点D，FG⊥AB于点G，∠1=∠2.求证：ED ∥ BC.【交流展示】变式：点评：方法1，利用平行线的判定和性质 方法2，利用三角形内角和定理2、如图，在△ABC中，∠ACB=90°，AE是角平分线，CD是高，AE、CD相交于点F.求证： ∠CFE= ∠CEF课堂练习：书本166页第10题【交流展示】专题三：三角形内角和定理及推论 （1）已知：如图①，若AB∥CD，点P在AB、CD内部时,∠BPD、∠B、∠D有何数量关系？ 请证明你的结论.变式一：在图① 中，将点P移到AB、CD外部，如图②，题（1）的结论还是否成立，若不成立，则BPD 、∠B、∠D之间有何数量关系？请证明你的结论.图②图①∠B= ∠BPD+ ∠D∠BPD = ∠B + ∠D【拓展延伸】专题三：三角形内角和定理及推论变式二：在图①中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q 如图③，则∠BPD 、 ∠B、 ∠D、∠BQD 之间有何数量关系？ ∠BPD= ∠B+∠D+∠BQD【交流展示】专题三：三角形内角和定理及推论 （2）如图(1)，在五角星图形中， 求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数。变式一：把图（2）、（3）叫蜕化的五角星，问它们的五角之和与五角星图形的五角之和仍相等吗？为什么？拓展延伸：专题三：三角形内角和定理及推论变式二：根据的上面的结论求图④中∠A+ ∠B+ ∠C+ ∠D+ ∠E+∠F的度数.∠A+ ∠B+ ∠C+ ∠D+ ∠E+∠F=360°拓展延伸：专题三：三角形内角和定理及推论【课堂小结】通过这节课的学习,你有哪些收获？第十二章 证明复习课