


所属成套资源:2023九年级数学下册新版湘教版 练习(17份)
初中数学湘教版九年级下册1.1 二次函数一课一练
展开
这是一份初中数学湘教版九年级下册1.1 二次函数一课一练,共9页。试卷主要包含了抛物线y=ax2+b等内容,欢迎下载使用。
《22.1.3 函数的图象与性质(一)》 一.选择题1.抛物线y=2x2﹣1的顶点坐标是( )A.(0,1) B.(0,﹣1) C.(1,0) D.(﹣1,0)2.抛物线y=ax2+b(a≠0)与x轴有两个交点,且开口向上,则a、b的取值范围是( )A.a>0,b<0 B.a>0,b>0 C.a<0,b<0 D.a<0,b>0![]() 3.小敏在某次投篮中,球的运动路线是抛物线y=
3.小敏在某次投篮中,球的运动路线是抛物线y=![]() x2+3.5的一部分(如图),若命中篮圈中心,则他与篮底的距离L是( )
x2+3.5的一部分(如图),若命中篮圈中心,则他与篮底的距离L是( )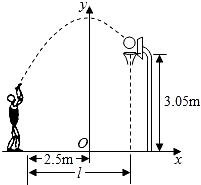
 A.3.5m B.4m C.4.5m D.4.6m4.抛物线y=2x2﹣3可以看作由抛物线y=2x2如何变换得到的( )A.向上平移3个单位长度 B.向下平移3个单位长度C.向左平移3个单位长度 D.向右平移3个单位长度5.抛物线y=﹣2x2+1的对称轴是( )
A.3.5m B.4m C.4.5m D.4.6m4.抛物线y=2x2﹣3可以看作由抛物线y=2x2如何变换得到的( )A.向上平移3个单位长度 B.向下平移3个单位长度C.向左平移3个单位长度 D.向右平移3个单位长度5.抛物线y=﹣2x2+1的对称轴是( )![]()
![]() A.直线
A.直线![]() B.直线
B.直线![]() C.y轴 D.直线x=26.抛物线y=x2﹣4与x轴交于B,C两点,顶点为A,则△ABC的周长为( )
C.y轴 D.直线x=26.抛物线y=x2﹣4与x轴交于B,C两点,顶点为A,则△ABC的周长为( )![]()
![]()
![]() A.4
A.4![]() B.4
B.4![]() +4 C.12 D.2
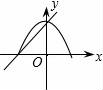
+4 C.12 D.2![]() +47.在同一平面直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致所示中的( )
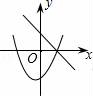
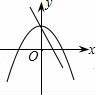
+47.在同一平面直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致所示中的( )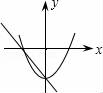
 A.
A. B.
B. C.
C. D.
D. 二.填空题8.函数y=ax2+c(a≠0)的图象是一条______,对称轴是______,顶点是______,当a>0,抛物线开口______,顶点是抛物线的______,当a<0,抛物线开口______,顶点是抛物线的______.9.抛物线y=﹣2x2﹣3的开口______,对称轴是______,顶点坐标是______,当x______时,y随x的增大而增大,当x______时,y随x的增大而减小.10.若二次函数y=ax2+c,当x取x1,x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值为______.11.任给一些不同的实数k,得到不同的抛物线y=x2+k,当k取0,±1时,关于这些抛物线有以下判断:①开口方向都相同;②对称轴都相同;③形状相同;④都有最底点.其中判断正确的是______.12.点A(3,m)在抛物线y=x2﹣1上,则点A关于x轴的对称点的坐标为______.13.若抛物线y=x2+(m﹣2)x+3的对称轴是y轴,则m=______.
二.填空题8.函数y=ax2+c(a≠0)的图象是一条______,对称轴是______,顶点是______,当a>0,抛物线开口______,顶点是抛物线的______,当a<0,抛物线开口______,顶点是抛物线的______.9.抛物线y=﹣2x2﹣3的开口______,对称轴是______,顶点坐标是______,当x______时,y随x的增大而增大,当x______时,y随x的增大而减小.10.若二次函数y=ax2+c,当x取x1,x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值为______.11.任给一些不同的实数k,得到不同的抛物线y=x2+k,当k取0,±1时,关于这些抛物线有以下判断:①开口方向都相同;②对称轴都相同;③形状相同;④都有最底点.其中判断正确的是______.12.点A(3,m)在抛物线y=x2﹣1上,则点A关于x轴的对称点的坐标为______.13.若抛物线y=x2+(m﹣2)x+3的对称轴是y轴,则m=______.![]() 14.若一条抛物线与y=
14.若一条抛物线与y=![]() 的形状相同且开口向上,顶点坐标为(0,2),则这条抛物线的解析式为______.
的形状相同且开口向上,顶点坐标为(0,2),则这条抛物线的解析式为______.![]() 15.与抛物线y=﹣
15.与抛物线y=﹣![]() +3关于x轴对称的抛物线的解析式为______.
+3关于x轴对称的抛物线的解析式为______.![]() 16.已知A(﹣1,y1),B(
16.已知A(﹣1,y1),B(![]() ,y2),C(2,y3)三点都在二次函数y=ax2﹣1(a>0)的图象上,那么y1,y2,y3的大小关系是______.(用“<”连接) 三.解答题17.已知抛物线y=ax2+b过点(﹣2,﹣3)和点(1,6)(1)求这个函数的关系式;(2)当为何值时,函数y随x的增大而增大.18.已知直线y=2x和抛物线y=ax2+3相交于点A(2,b),求a,b的值.19.如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形其面积为8,此抛物线的解析式.
,y2),C(2,y3)三点都在二次函数y=ax2﹣1(a>0)的图象上,那么y1,y2,y3的大小关系是______.(用“<”连接) 三.解答题17.已知抛物线y=ax2+b过点(﹣2,﹣3)和点(1,6)(1)求这个函数的关系式;(2)当为何值时,函数y随x的增大而增大.18.已知直线y=2x和抛物线y=ax2+3相交于点A(2,b),求a,b的值.19.如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形其面积为8,此抛物线的解析式.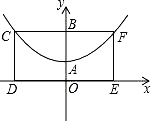
 《22.1.3 函数的图象与性质(一)》参考答案 一.选择题1.抛物线y=2x2﹣1的顶点坐标是( )A.(0,1) B.(0,﹣1) C.(1,0) D.(﹣1,0)【解答】解:抛物线y=2x2﹣1的顶点坐标为(0,﹣1).故选:B. 2.抛物线y=ax2+b(a≠0)与x轴有两个交点,且开口向上,则a、b的取值范围是( )A.a>0,b<0 B.a>0,b>0 C.a<0,b<0 D.a<0,b>0【解答】解:∵开口向上,∴a>0;∵抛物线y=ax2+b(a≠0)与x轴有两个交点,∴0﹣4ab>0,∴b<0.故选A.
《22.1.3 函数的图象与性质(一)》参考答案 一.选择题1.抛物线y=2x2﹣1的顶点坐标是( )A.(0,1) B.(0,﹣1) C.(1,0) D.(﹣1,0)【解答】解:抛物线y=2x2﹣1的顶点坐标为(0,﹣1).故选:B. 2.抛物线y=ax2+b(a≠0)与x轴有两个交点,且开口向上,则a、b的取值范围是( )A.a>0,b<0 B.a>0,b>0 C.a<0,b<0 D.a<0,b>0【解答】解:∵开口向上,∴a>0;∵抛物线y=ax2+b(a≠0)与x轴有两个交点,∴0﹣4ab>0,∴b<0.故选A. ![]() 3.小敏在某次投篮中,球的运动路线是抛物线y=
3.小敏在某次投篮中,球的运动路线是抛物线y=![]() x2+3.5的一部分(如图),若命中篮圈中心,则他与篮底的距离L是( )
x2+3.5的一部分(如图),若命中篮圈中心,则他与篮底的距离L是( )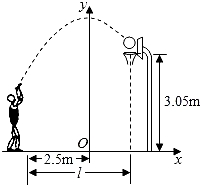
 A.3.5m B.4m C.4.5m D.4.6m
A.3.5m B.4m C.4.5m D.4.6m![]() 【解答】解:如图,把C点纵坐标y=3.05代入y=
【解答】解:如图,把C点纵坐标y=3.05代入y=![]() x2+3.5中得:x=±1.5(舍去负值),即OB=1.5,所以l=AB=2.5+1.5=4.
x2+3.5中得:x=±1.5(舍去负值),即OB=1.5,所以l=AB=2.5+1.5=4.![]() 令解:把y=3.05代入y=﹣
令解:把y=3.05代入y=﹣![]() x2+3.5中得:x1=1.5,x2=﹣1.5(舍去),∴L=2.5+1.5=4米.故选:B.
x2+3.5中得:x1=1.5,x2=﹣1.5(舍去),∴L=2.5+1.5=4米.故选:B.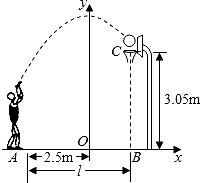
 4.抛物线y=2x2﹣3可以看作由抛物线y=2x2如何变换得到的( )A.向上平移3个单位长度 B.向下平移3个单位长度C.向左平移3个单位长度 D.向右平移3个单位长度【解答】解:∵抛物线y=2x2﹣3顶点坐标为(0,﹣3),抛物线y=2x2顶点坐标为(0,0),∴抛物线y=2x2﹣3可以看作由抛物线y=2x2向下平移3个单位长度得到的,故选B. 5.抛物线y=﹣2x2+1的对称轴是( )
4.抛物线y=2x2﹣3可以看作由抛物线y=2x2如何变换得到的( )A.向上平移3个单位长度 B.向下平移3个单位长度C.向左平移3个单位长度 D.向右平移3个单位长度【解答】解:∵抛物线y=2x2﹣3顶点坐标为(0,﹣3),抛物线y=2x2顶点坐标为(0,0),∴抛物线y=2x2﹣3可以看作由抛物线y=2x2向下平移3个单位长度得到的,故选B. 5.抛物线y=﹣2x2+1的对称轴是( )![]()
![]() A.直线
A.直线![]() B.直线
B.直线![]() C.y轴 D.直线x=2【解答】解:∵抛物线y=﹣2x2+1的顶点坐标为(0,1),∴对称轴是直线x=0(y轴),故选C. 6.抛物线y=x2﹣4与x轴交于B,C两点,顶点为A,则△ABC的周长为( )
C.y轴 D.直线x=2【解答】解:∵抛物线y=﹣2x2+1的顶点坐标为(0,1),∴对称轴是直线x=0(y轴),故选C. 6.抛物线y=x2﹣4与x轴交于B,C两点,顶点为A,则△ABC的周长为( )![]()
![]()
![]() A.4
A.4![]() B.4
B.4![]() +4 C.12 D.2
+4 C.12 D.2![]() +4【解答】解:∵抛物线y=x2﹣4与x轴交于B、C两点,顶点为A,∴B(﹣2,0),C(2,0),A(0,﹣4).
+4【解答】解:∵抛物线y=x2﹣4与x轴交于B、C两点,顶点为A,∴B(﹣2,0),C(2,0),A(0,﹣4).![]()
![]() ∴AB=4,BC=AC=
∴AB=4,BC=AC=![]() =2
=2![]() ,
,![]() ∴△ABC周长为:AB+BC+AC=4+4
∴△ABC周长为:AB+BC+AC=4+4![]() .故应选B. 7.在同一平面直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致所示中的( )
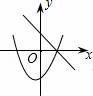
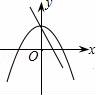
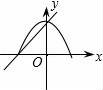
.故应选B. 7.在同一平面直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致所示中的( )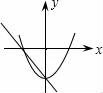
 A.
A. B.
B. C.
C. D.
D. 【解答】解:A、由一次函数的图象可知a>0 c>0,由二次函数的图象可知a<0,两者相矛盾;B、由一次函数的图象可知a<0 c>0,由二次函数的图象可知a<0,两者相吻合;C、由一次函数的图象可知a<0 c>0,由二次函数的图象可知a>0,两者相矛盾;D、由一次函数的图象可知a<0 c<0,由二次函数的图象可知a>0,两者相矛盾.故选B. 二.填空题8.函数y=ax2+c(a≠0)的图象是一条 抛物线 ,对称轴是 y轴 ,顶点是 (0,c) ,当a>0,抛物线开口 向上 ,顶点是抛物线的 最低点 ,当a<0,抛物线开口 向下 ,顶点是抛物线的 最高点 .【解答】解:函数y=ax2+c(a≠0)的图象是一条抛物线,对称轴是y轴,顶点是(0,c),当a>0,抛物线开口向上,顶点是抛物线的最低点,当a<0,抛物线开口向下,顶点是抛物线的最高点.故答案为:抛物线,y轴,(0,c),向上,最低点,向下,最高点. 9.抛物线y=﹣2x2﹣3的开口 向下 ,对称轴是 y轴 ,顶点坐标是 (0,﹣3) ,当x <0 时,y随x的增大而增大,当x >0 时,y随x的增大而减小.【解答】解:抛物线y=﹣2x2﹣3的开口向下,对称轴是y轴,顶点坐标是(0,﹣3),当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小.故答案为:向下,y轴,(0,﹣3),<0,>0. 10.若二次函数y=ax2+c,当x取x1,x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值为 c .【解答】解:∵在y=ax2+c中,当x取x1,x2(x1≠x2)时,函数值相等,∴抛物线的对称轴是y轴,∴x1,x2互为相反数,∴x1+x2=0,当x=0时,y=c.故填空答案:c. 11.任给一些不同的实数k,得到不同的抛物线y=x2+k,当k取0,±1时,关于这些抛物线有以下判断:①开口方向都相同;②对称轴都相同;③形状相同;④都有最底点.其中判断正确的是 ①②③④ .【解答】解:抛物线y=x2+k,当k取0,±1时,关于这些抛物线有以下判断:①开口方向都向上,故相同,正确;②对称轴都是y轴,故相同;正确,③形状相同;正确,④都有最底点.正确.其中判断正确的是①②③④.故答案为:①②③④ 12.点A(3,m)在抛物线y=x2﹣1上,则点A关于x轴的对称点的坐标为 (3,﹣8) .【解答】解:∵A(3,m)在抛物线y=x2﹣1上,∴m=9﹣1=8,∴A点坐标为(3,8),∴点A关于x轴的对称点的坐标为(3,﹣8).故答案为(3,﹣8). 13.若抛物线y=x2+(m﹣2)x+3的对称轴是y轴,则m= 2 .【解答】解:∵y=x2+(m﹣2)x+3,
【解答】解:A、由一次函数的图象可知a>0 c>0,由二次函数的图象可知a<0,两者相矛盾;B、由一次函数的图象可知a<0 c>0,由二次函数的图象可知a<0,两者相吻合;C、由一次函数的图象可知a<0 c>0,由二次函数的图象可知a>0,两者相矛盾;D、由一次函数的图象可知a<0 c<0,由二次函数的图象可知a>0,两者相矛盾.故选B. 二.填空题8.函数y=ax2+c(a≠0)的图象是一条 抛物线 ,对称轴是 y轴 ,顶点是 (0,c) ,当a>0,抛物线开口 向上 ,顶点是抛物线的 最低点 ,当a<0,抛物线开口 向下 ,顶点是抛物线的 最高点 .【解答】解:函数y=ax2+c(a≠0)的图象是一条抛物线,对称轴是y轴,顶点是(0,c),当a>0,抛物线开口向上,顶点是抛物线的最低点,当a<0,抛物线开口向下,顶点是抛物线的最高点.故答案为:抛物线,y轴,(0,c),向上,最低点,向下,最高点. 9.抛物线y=﹣2x2﹣3的开口 向下 ,对称轴是 y轴 ,顶点坐标是 (0,﹣3) ,当x <0 时,y随x的增大而增大,当x >0 时,y随x的增大而减小.【解答】解:抛物线y=﹣2x2﹣3的开口向下,对称轴是y轴,顶点坐标是(0,﹣3),当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小.故答案为:向下,y轴,(0,﹣3),<0,>0. 10.若二次函数y=ax2+c,当x取x1,x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值为 c .【解答】解:∵在y=ax2+c中,当x取x1,x2(x1≠x2)时,函数值相等,∴抛物线的对称轴是y轴,∴x1,x2互为相反数,∴x1+x2=0,当x=0时,y=c.故填空答案:c. 11.任给一些不同的实数k,得到不同的抛物线y=x2+k,当k取0,±1时,关于这些抛物线有以下判断:①开口方向都相同;②对称轴都相同;③形状相同;④都有最底点.其中判断正确的是 ①②③④ .【解答】解:抛物线y=x2+k,当k取0,±1时,关于这些抛物线有以下判断:①开口方向都向上,故相同,正确;②对称轴都是y轴,故相同;正确,③形状相同;正确,④都有最底点.正确.其中判断正确的是①②③④.故答案为:①②③④ 12.点A(3,m)在抛物线y=x2﹣1上,则点A关于x轴的对称点的坐标为 (3,﹣8) .【解答】解:∵A(3,m)在抛物线y=x2﹣1上,∴m=9﹣1=8,∴A点坐标为(3,8),∴点A关于x轴的对称点的坐标为(3,﹣8).故答案为(3,﹣8). 13.若抛物线y=x2+(m﹣2)x+3的对称轴是y轴,则m= 2 .【解答】解:∵y=x2+(m﹣2)x+3,![]() ∴其对称轴方程为x=﹣
∴其对称轴方程为x=﹣![]() ,∵其对称轴为y轴,
,∵其对称轴为y轴,![]() ∴﹣
∴﹣![]() =0,解得m=2,故答案为:2.
=0,解得m=2,故答案为:2. ![]()
![]() 14.若一条抛物线与y=
14.若一条抛物线与y=![]() 的形状相同且开口向上,顶点坐标为(0,2),则这条抛物线的解析式为 y=
的形状相同且开口向上,顶点坐标为(0,2),则这条抛物线的解析式为 y=![]() x2+2 .
x2+2 .![]() 【解答】解:根据题意设抛物线解析式为y=
【解答】解:根据题意设抛物线解析式为y=![]() x2+b,把x=0,y=2代入得:2=b,
x2+b,把x=0,y=2代入得:2=b,![]() 则抛物线解析式为y=
则抛物线解析式为y=![]() x2+2,
x2+2,![]() 故答案为:y=
故答案为:y=![]() x2+2
x2+2 ![]()
![]() 15.与抛物线y=﹣
15.与抛物线y=﹣![]() +3关于x轴对称的抛物线的解析式为 y=
+3关于x轴对称的抛物线的解析式为 y=![]() x2﹣3 .
x2﹣3 .![]() 【解答】解:y=﹣
【解答】解:y=﹣![]() +3的顶点坐标为(0,3),而点(0,3)关于x轴对称的点的坐标为(0,﹣3),
+3的顶点坐标为(0,3),而点(0,3)关于x轴对称的点的坐标为(0,﹣3),![]()
![]() 所以抛物线y=﹣
所以抛物线y=﹣![]() +3关于x轴对称后抛物线的解析式为y=
+3关于x轴对称后抛物线的解析式为y=![]() x2﹣3.
x2﹣3.![]() 故答案为y=
故答案为y=![]() x2﹣3.
x2﹣3. ![]() 16.已知A(﹣1,y1),B(
16.已知A(﹣1,y1),B(![]() ,y2),C(2,y3)三点都在二次函数y=ax2﹣1(a>0)的图象上,那么y1,y2,y3的大小关系是 y1<y2<y3 .(用“<”连接)【解答】解:∵二次函数的解析式为y=ax2﹣1(a>0),∴抛物线的对称轴为直线x=0,
,y2),C(2,y3)三点都在二次函数y=ax2﹣1(a>0)的图象上,那么y1,y2,y3的大小关系是 y1<y2<y3 .(用“<”连接)【解答】解:∵二次函数的解析式为y=ax2﹣1(a>0),∴抛物线的对称轴为直线x=0,![]() ∵A(﹣1,y1)、B(
∵A(﹣1,y1)、B(![]() ,y2)、C(2,y3),∴点C离直线x=0最远,点A离直线x=0最近,而抛物线开口向上,∴y1<y2<y3.故答案为y1<y2<y3. 三.解答题17.已知抛物线y=ax2+b过点(﹣2,﹣3)和点(1,6)(1)求这个函数的关系式;(2)当为何值时,函数y随x的增大而增大.【解答】解:(1)把点(﹣2,﹣3)和点(1,6)代入y=ax2+b得
,y2)、C(2,y3),∴点C离直线x=0最远,点A离直线x=0最近,而抛物线开口向上,∴y1<y2<y3.故答案为y1<y2<y3. 三.解答题17.已知抛物线y=ax2+b过点(﹣2,﹣3)和点(1,6)(1)求这个函数的关系式;(2)当为何值时,函数y随x的增大而增大.【解答】解:(1)把点(﹣2,﹣3)和点(1,6)代入y=ax2+b得![]()
![]()
![]() ,解得
,解得![]() 所以这个函数的关系式为y=﹣3x2+9;(2)∵这个函数的关系式为y=﹣3x2+9;∴对称轴x=0,∵a=﹣3<0,∴抛物线开口向下,∴当x<0时,函数y随x的增大而增大. 18.已知直线y=2x和抛物线y=ax2+3相交于点A(2,b),求a,b的值.【解答】解:把A(2,b)代入y=2x得b=2×2=4,则A点坐标为(2,4),
所以这个函数的关系式为y=﹣3x2+9;(2)∵这个函数的关系式为y=﹣3x2+9;∴对称轴x=0,∵a=﹣3<0,∴抛物线开口向下,∴当x<0时,函数y随x的增大而增大. 18.已知直线y=2x和抛物线y=ax2+3相交于点A(2,b),求a,b的值.【解答】解:把A(2,b)代入y=2x得b=2×2=4,则A点坐标为(2,4),![]() 把A(2,4)代入y=ax2+3得4a+3=4,解得a=
把A(2,4)代入y=ax2+3得4a+3=4,解得a=![]() . 19.如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形其面积为8,此抛物线的解析式.
. 19.如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形其面积为8,此抛物线的解析式.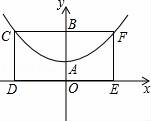
 【解答】解:∵抛物线的顶点为A(0,1),∴抛物线的对称轴为y轴,∵四边形CDEF为矩形,∴C、F点为抛物线上的对称点,∵矩形其面积为8,OB=2∴CF=4,∴F点的坐标为(2,2),设抛物线解析式为y=ax2+1,
【解答】解:∵抛物线的顶点为A(0,1),∴抛物线的对称轴为y轴,∵四边形CDEF为矩形,∴C、F点为抛物线上的对称点,∵矩形其面积为8,OB=2∴CF=4,∴F点的坐标为(2,2),设抛物线解析式为y=ax2+1,![]() 把F(2,2)代入得4a+1=2,解得a=
把F(2,2)代入得4a+1=2,解得a=![]() ,
,![]() ∴抛物线解析式为y=
∴抛物线解析式为y=![]() x2+1.
x2+1.
相关试卷
这是一份初中数学人教版九年级上册22.1.1 二次函数第3课时同步测试题,共5页。试卷主要包含了抛物线 经过点., 6等内容,欢迎下载使用。
这是一份初中数学人教版九年级上册22.1.1 二次函数第1课时同步测试题,共7页。试卷主要包含了二次函数的定义,下列函数中, 若是关于的二次函数,则,适合解析式的一对值是等内容,欢迎下载使用。
这是一份湘教版八年级下册4.2 一次函数练习题,共6页。试卷主要包含了正比例函数y=3x的大致图像是,正比例函数y=-x的图象平分等内容,欢迎下载使用。










