2023八年级数学下册第2章四边形平行四边形性质同步练习新版湘教版

2.2.1平行四边形性质同步练习

一、选择题(本大题共8小题)

1.在▱ABCD中，下列结论一定正确的是（　　）

A．AC⊥BD    B．∠A+∠B=180°    C．AB=AD     D．∠A≠∠C

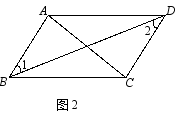
2. 如图2，在平行四边形ABCD中，下列结论中错误的是（  ）

A．∠1=∠2      B．∠BAD=∠BCD     C．AB=CD  D． AC⊥BD

3. 如图，在▱ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，AB=6，EF=2，则BC长为（　　）

A．8      B．10     C．12      D．14

4. 如图，在▱ABCD中，AB=4，BC=6，∠B=30°，则此平行四边形的面积是（　　）

A. 6      B. 12       C. 18     D. 24

5 .如图，▱ABCD的对角线AC、BD相交于点O，且AC+BD=16，CD=6，则△ABO的周长是（　　）

A．10     B．14     C．20     D．22

6. 如图，在▱ABCD中，延长AB到点E，使BE=AB，连接DE交BC于点F，则下列结论不一定成立的是（　　）

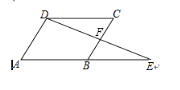
1. ∠E=∠CDF    B. EF=DF      C. AD=2BF     D. BE=2CF

7. 如图，在□ABCD中，E为边CD上一点，将△ADE沿AE折叠至△AD′E处，AD′与CE交于点F．若∠B＝52°，∠DAE＝20°，则∠FED′的大小为_______．

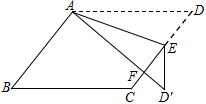
A．36°     B．52°          C．48°         D．30°

8. 如图，在平行四边形ABCD中，AB＝4，∠BAD的平分线与BC的延长线交于点E，与DC交于点F，且点F为边DC的中点，DG⊥AE，垂足为G，若DG＝1，则AE的边长为（　　）

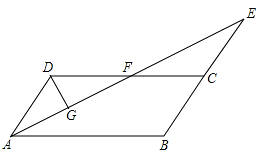
A．2        B．4           C．4          D．8

二、填空题(本大题共6小题)

9. 如图所示，在□ABCD中，两条对角线交于点O，有△AOB≌△_____，△AOD≌△_____．

10. 在□ABCD中，∠A：∠B＝2：3，则∠B＝____，∠C＝_____，∠D＝____．

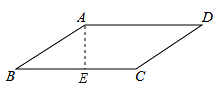
11. 在▱ABCD中，BC边上的高为4，AB=5，AC=2 ，则▱ABCD的周长等于　   　．

12. 如图所示，在▱ABCD中，∠C=40°，过点D作AD的垂线，交AB于点E，交CB的延长线于点F，则∠BEF的度数为   　．

13. 如图，□ ABCD中，E是BA延长线上一点，AB＝AE，连结CE交AD于点F，若CF平分∠BCD，AB＝3，则BC的长为        ．

14. 如图，□ABCD的周长为36．对角线AC，BD相交于点O．点E是CD的中点．BO=12．则△DOE的周长为__________________.

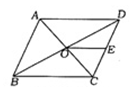
三、计算题(本大题共4小题)

15. 已知平行四边形ABCD中，CE平分∠BCD且交AD于点E，AF∥CE，且交BC于点F．

（1）求证：△ABF≌△CDE；

（2）如图，若∠1=65°，求∠B的大小．

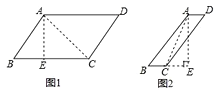
16. 图1，图2都是8×8的正方形网格，每个小正方形的顶点成为格点，每个小正方形的边长均为1，在每个正方形网格中标注了6个格点，这6个格点简称为标注点

（1）请在图1，图2中，以4个标注点为顶点，各画一个平行四边形（两个平行四边形不全等）；

（2）图1中所画的平行四边形的面积为　 　．

17. 如图，在▱ABCD中，连接BD，在BD的延长线上取一点E，在DB的延长线上取一点F，使BF=DE，连接AF、CE．

求证：AF∥CE．

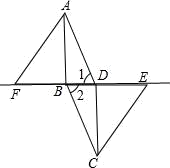
18. 如图，平行四边形ABCD的对角线AC、BD相交于点O，E，F分别是OA，OC的中点，连接BE，DF

（1）根据题意，补全原形；

（2）求证：BE=DF．

参考答案：

一、选择题(本大题共8小题)

1. B

分析：此题考查了平行四边形的性质．

解：∵四边形ABCD是平行四边形，

∴AD∥BC，

∴∠A+∠B=180°．故选B

2. D

分析：根据平行四边形性质可知：平行四边形的对边相等，平行四边形的对角相等，平行四边形的对角线互相平分。

解：根据平行四边形的性质可知D是错误的。

3. B

分析：由平行四边形的性质和角平分线得出∠ABF=∠AFB，得出AF=AB=6，同理可证DE=DC=6，再由EF的长，即可求出BC的长．

解：∵四边形ABCD是平行四边形，

∴AD∥BC，DC=AB=6，AD=BC，

∴∠AFB=∠FBC，

∵BF平分∠ABC，

∴∠ABF=∠FBC，

则∠ABF=∠AFB，

∴AF=AB=6，

同理可证：DE=DC=6，

∵EF=AF+DE﹣AD=2，

即6+6﹣AD=2，

解得：AD=10；

故选：B．

4. B

分析：过点A作AE⊥BC于E，根据含30度角的直角三角形的性质：在直角三角形中，30°角所对的直角边等于斜边的一半可求出AE的长，利用平行四边形的面积根据即可求出其面积．

解：过点A作AE⊥BC于E，

∵直角△ABE中，∠B=30°，

∴AE=AB=×4=2

∴平行四边形ABCD面积=BC•AE=6×2=12，

故选B．

5 .B

分析：直接利用平行四边形的性质得出AO=CO，BO=DO，DC=AB=6，再利用已知求出AO+BO的长，进而得出答案．

解：∵四边形ABCD是平行四边形，

∴AO=CO，BO=DO，DC=AB=6，

∵AC+BD=16，

∴AO+BO=8，

∴△ABO的周长是：14．

故选：B．

6. D

分析：首先根据平行四边形的性质可得CD∥AB，再根据平行线的性质可得∠E=∠CDF；首先证明△DCF≌△EBF可得EF=DF；根据全等可得CF=BF=BC，再利用等量代换可得AD=2BF；根据题意不能证明AD=BE，因此BE不一定等于2CF．

解：∵四边形ABCD是平行四边形，

∴CD∥AB，

∴∠E=∠CDF，故A成立；

∵四边形ABCD是平行四边形，

∴CD=AB，CD∥BE，

∴∠C=∠CBE，

∵BE=AB，

∴CD=EB，

在△CDF和△BEF中，

，

∴△DCF≌△EBF（AAS），

∴EF=DF，故B成立；

∵△DCF≌△EBF，

∴CF=BF=BC，

∵AD=BC，

∴AD=2BF，故C成立；

∵AD≠BE，

∴2CF≠BE，故D不成立；

故选：D．

7. A

分析：利用平行四边形的性质来解答即可。

解：∵四边形ABCD为平行四边形，∴∠D＝∠B＝52°，由折叠的性质得：∠EAD，＝∠DAE＝20°，∠AED，＝∠AED＝180°－∠DAE－∠D＝180°－20°－52°＝108°，

∴∠AEF＝∠D＋∠DAE＝52°＋20°＝72°，∴∠FED′＝108°－72°＝36°．故选A。

8. B

分析：由AE为角平分线，得到一对角相等，再由ABCD为平行四边形，得到AD与BE平行，利用两直线平行内错角相等得到一对角相等，等量代换及等角对等边得到AD＝DF，由F为DC中点，AB＝CD，求出AD与DF的长，得出三角形ADF为等腰三角形，根据三线合一得到G为AF中点，在直角三角形ADG中，由AD与DG的长，利用勾股定理求出AG的长，进而求出AF的长，再由三角形ADF与三角形ECF全等，得出AF＝EF，即可求出AE的长．

解：∵AE为∠ADB的平分线，∴∠DAE＝∠BAE，

∵DC∥AB，∴∠BAE＝∠DFA，∴∠DAE＝∠DFA，∴AD＝FD，

又F为DC的中点，∴DF＝CF，∴AD＝DF＝DC＝AB＝2，

在Rt△ADG中，根据勾股定理得：AG＝，则AF＝2AG＝2 ，

在△ADF和△ECF中，

，

∴△ADF≌△ECF（AAS），∴AF＝EF，则AE＝2AF＝4 ．故选B。

二、填空题(本大题共6小题)

9. 分析：运用平行四边形的性质定理和全都三角形的判定定理即可.

解：∵在□ABCD中，两条对角线交于点O，∴AB=CD，AD=BC，AO=CO， BO=DO，∴△AOB≌△COD，△AOD≌△COB．故答案为△COD，△COB.

10. 分析：直接运用平行四边形的性质定理即可.

解：∵□ABCD中，∠A+∠B=180°，又∵∠A：∠B=2：3，∴∠A=72°，∠B=108°．∴∠D=∠B=108°，∠C=∠A=72°．

11.分析：根据题意分别画出图形，BC边上的高在平行四边形的内部和外部，进而利用勾股定理求出即可．

解：如图1所示：

∵在▱ABCD中，BC边上的高为4，AB=5，AC=2 ，

∴EC= =2，AB=CD=5，

BE= =3，

∴AD=BC=5，

∴▱ABCD的周长等于：20，

如图2所示：

∵在▱ABCD中，BC边上的高为4，AB=5，AC=2 ，

∴EC= =2，AB=CD=5，

BE= =3，

∴BC=3﹣2=1，

∴▱ABCD的周长等于：1+1+5+5=12，

则▱ABCD的周长等于12或20．

故答案为：12或20．

12. 分析：由“平行四边形的对边相互平行”、“两直线平行，同位角相等”以及“直角三角形的两个锐角互余”的性质进行解答．

解：∵四边形ABCD是平行四边形，

∴DC∥AB，

∴∠C=∠ABF．

又∵∠C=40°，

∴∠ABF=40°．

∵EF⊥BF，

∴∠F=90°，

∴∠BEF=90°﹣40°=50°．

故答案是：50°．

13. 解：∵若CF平分∠BCD，∴∠BCE=∠DCF，∵AD∥BC，∴∠BCE=∠DFC，

∴∠BCE=∠EFA，∵BE∥CD，∴∠E=∠DCF，∴∠E=∠BCE，∵AD∥BC，∴∠BCE=∠EFA，

∴∠E=∠EFA，∴AE=AF=AB=3，∵AB=AE，AF∥BC，∴BC=2AF=6．

14. 分析：根据平行四边形的性质，对角线互相平分，两组对边分别相等，可以分别求出OD、OE+DE的长，即可求解.

解：∵□ABCD的周长为36，∴BC+CD=18，∵四边形ABCD为平行四边形，∴O是BD的中点，∴OD=6,又∵E是CD的中点，∴OE是△BCD的中位线，∴OE+DE=9，∴△DOE的周长=OD+OE+DE

=6+9

=15

三、计算题(本大题共4小题)

15. 分析：（1）由平行四边形的性质得出AB=CD，AD∥BC，∠B=∠D，得出∠1=∠DCE，证出∠AFB=∠1，由AAS证明△ABF≌△CDE即可；

（2）由（1）得∠1=∠DCE=65°，由平行四边形的性质和三角形内角和定理即可得出结果．

解：（1）证明：∵四边形ABCD是平行四边形，

∴AB=CD，AD∥BC，∠B=∠D，∴∠1=∠DCE，

∵AF∥CE，∴∠AFB=∠ECB，

∵CE平分∠BCD，∴∠DCE=∠ECB，∴∠AFB=∠1，

在△ABF和△CDE中，，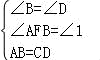

∴△ABF≌△CDE（AAS）；

（2）解：由（1）得：∠1=∠ECB，∠DCE=∠ECB，

∴∠1=∠DCE=65°，

∴∠B=∠D=180°﹣2×65°=50°．

16. 分析：（1）根据平行四边形的判定，利用一组对边平行且相等的四边形为平行四边形可在图1和图2中按要求画出平行四边形；

（2）根据平行四边形的面积公式计算．

解：（1）如图1，如图2；

（2）图1中所画的平行四边形的面积=2×3=6．

故答案为6．

17. 分析：由平行四边形的性质得出AD∥BC，AD=BC，证出∠1=∠2，DF=BE，由SAS证明△ADF≌△CBE，得出对应角相等，再由平行线的判定即可得出结论．

证明：∵四边形ABCD是平行四边形，

∴AD∥BC，AD=BC，

∴∠1=∠2，

∵BF=DE，

∴BF+BD=DE+BD，

即DF=BE，

在△ADF和△CBE中，

，

∴△ADF≌△CBE（SAS），

∴∠AFD=∠CEB，

∴AF∥CE．

18. 分析：（1）如图所示；

（2）由全等三角形的判定定理SAS证得△BEO≌△DFO，得出全等三角形的对应边相等即可．

解：1）解：如图所示：

（2）证明：∵四边形ABCD是平行四边形，对角线AC、BD交于点O，

∴OB=OD，OA=OC．

又∵E，F分别是OA、OC的中点，

∴OE=OA，OF=OC，

∴OE=OF．

∵在△BEO与△DFO中，，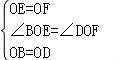

∴△BEO≌△DFO（SAS），

∴BE=DF．