2023年青岛版数学八年级上册《5.4 平行线的性质定理和判定定理》课时练习（含答案）

2023年青岛版数学八年级上册

《5.4 平行线的性质定理和判定定理》课时练习

一              、选择题

1.如图，直线a、b被直线c所截，下列条件能使a∥b的是（     ）

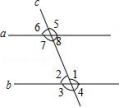
A.∠1=∠6        B.∠2=∠6         C.∠1=∠3     D.∠5=∠7

2.如图，下列条件中不能判断直线a∥b的是(　　)

A.∠1＝∠2                  B.∠3＝∠4                 C.∠2＝∠3                D.∠5＋∠6＝180°

3.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来方向上平行行驶,则这两次拐弯的角度应为（     ）

A.第一次向右拐38°，第二次向左拐142°

B.第一次向左拐38°，第二次向右拐38°

C.第一次向左拐38°，第二次向左拐142°

D.第一次向右拐38°，第二次向右拐40°

4.下列说法错误的是（     ）

A.内错角相等，两直线平行       B.两直线平行，同旁内角互补

C.同角的补角相等               D.相等的角是对顶角

5.如图，AB∥CD，直线MN与AB、CD分别交于点E和点F，GE⊥MN，∠1＝130°，则∠2等于(    )

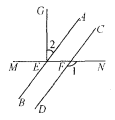
A.50°    B.40°    C.30°    D.65°

6.两条平行线被第三条直线所截，一对同旁内角的比为2：7，则这两个角中较大的角的度数为(   )           

A.40°      B.70°     C.100°    D.140°

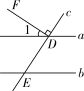
7.如图，直线a∥b，直线c与直线a，b分别交于点D，E，射线DF⊥直线c，则图中与∠1互余的角有(　　)

A.4个       B.3个        C.2个        D.1个

8.如图，直线11∥12，∠1=30°，则∠2+∠3=(　　)

A．150°      B．180°      C．210°      D．240°

二              、填空题

9.如图，利用直尺和三角尺过直线外一点画已知直线的平行线，这种画法依据的是　   　.

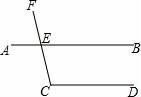
10.如图，已知AB与CF相交于点E，∠AEF=80°，要使AB∥CD，需要添加的一个条件是　   　.

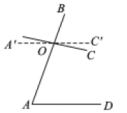
11.如图,∠A=700,O是AB上一点,直线CO与AB所夹的∠BOC=820.当直线OC绕点O按逆时针方向旋转        时，OC//AD.

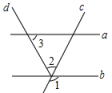
12.如图，a∥b，∠1＝110°，∠3＝40°，则∠2＝　   　.

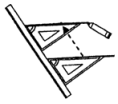
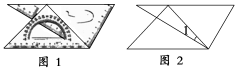
13.已知一副三角板如图1摆放，其中两条斜边互相平行，则图2中∠1＝________.

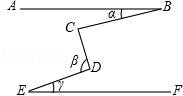
14.如图，已知AB∥EF，∠C=90°，则α、β与γ的关系是　    　.

三              、解答题

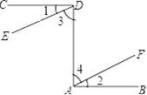
15.如图,已知CD⊥DA，DA⊥AB,∠1=∠2,问直线DE与AF是否平行？为什么？

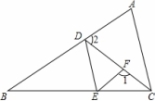
16.如图,已知∠1＋∠2=180°,∠DEF=∠A,试判断∠ACB与∠DEB的大小关系，并证明.

17.如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数．

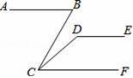
18.如图，在△ABC中，D，E，F分别为AB，AC，BC上的点，且DE∥BC，EF∥AB.

求证：∠ADE=∠EFC.

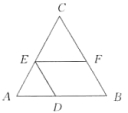
19.如图，EF⊥BC，AD⊥BC，∠1＝∠2，∠B＝30°．求∠GDB的度数．

请将求∠GDB度数的过程填写完整．

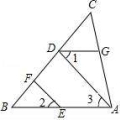
解：因为EF⊥BC，AD⊥BC，

所以∠BFE＝90°，∠BDA＝90°，理由是　       　，

即∠BFE＝∠BDA，所以EF∥　  　，理由是　         　，

所以∠2＝　   　，理由是　           　．

因为∠1＝∠2，所以∠1＝∠3，

所以AB∥　  　，理由是　                 　，

所以∠B+　  　＝180°，理由是　                　．

又因为∠B＝30°，所以∠GDB＝           ．

20.已知一个角的两边与另一个角的两边分别平行，请结合图①②探索这两个角之间的关系.

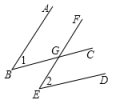
(1)如图①，AB∥CD，BE∥DF，则∠1与∠2的关系是            ；

(2)如图②，AB∥CD，BE∥DF，则∠1与∠2的关系是             ；并说明理由；

(3) 由此得出结论，如果两个角的两边分别平行，那么这两个角            ；　

(4) 若两个角的两边分别平行，且一个角比另一个角的3倍少60°，则这两个角分别为多少度？

参考答案

1.B

2.B

3.B

4.D

5.B

6.D

7.A.

8.C

9.答案为：同位角相等，两直线平行.

10.答案为：∠C=100°.

11.答案为：12°；

12.答案为：70°.

13.答案为：15°.

14.答案为:α+β﹣γ=90°.

15.解：DE∥AF，理由如下：

∵CD⊥DA，DA⊥AB，

∴∠CDA=∠DAB=90°，

∴CD∥AB，

∵∠1=∠2，

∴∠CDA﹣∠1=∠DAB﹣∠2，

∴∠3=∠4，

∴DE∥AF．

16.解：∠ACB与∠DEB相等，理由如下：
证明：∵∠1+∠2=180°（已知），∠1+∠DFE=180°（邻补角定义），
∴∠2=∠DFE（同角的补角相等），
∴AB∥EF（内错角相等两直线平行），
∴∠BDE=∠DEF（两直线平行，内错角相等），
∵∠DEF=∠A（已知），
∴∠BDE=∠A（等量代换），
∴DE∥AC（同位角相等两直线平行），
∴∠ACB=∠DEB（两直线平行，同位角相等）．

17.解：∵AB∥CF，∠ABC=70°，

∴∠BCF=∠ABC=70°，

又∵DE∥CF，∠CDE=130°，

∴∠DCF+∠CDE=180°，

∴∠DCF=50°，

∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°．

18.证明：∵DE∥BC(已知)，

∴∠ADE=∠B(两直线平行.同位角相等).

又∵EF∥AB(已知)，

∴∠EFC=∠B(两直线平行，同位角相等).

∴∠ADE=∠EFC(等量代换).

19.答案为：垂直的定义，AD，同位角相等，两直线平行，∠3，两直线平行，同位角相等，DG，内错角相等，两直线平行，∠GDB，两直线平行，同旁内角互补，150°．

20.解：(1)相等；

(2)互补；

∵ AB∥CD(已知)

∴∠1＝∠3(两直线平行，内错角相等)

∵ BE∥DF(已知)

∴∠2＋∠3＝180°(两直线平行，同旁内角互补)

∴ ∠1＋∠2＝180°(等量代换)

(3)相等或互补；

(4)30°，30°；或60°，120°；

解：设一个角为x，则另一个角为3x-60°，

①由x＝3x-60°得：x＝30°，3x-60°＝30°

②由x＋3x-60°＝180°得：x＝60°，3x-60°＝120°

∴ 这两个角分别30°，30°或60°，120°；