2022-2023学年辽宁省沈阳市于洪区七年级（下）期末数学试卷（含解析）

这是一份2022-2023学年辽宁省沈阳市于洪区七年级（下）期末数学试卷（含解析），共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年辽宁省沈阳市于洪区七年级（下）期末数学试卷
一、选择题（本大题共10小题，共20.0分。在每小题列出的选项中，选出符合题目的一项）
1. 下列运算正确的是(    )
A. x2⋅x4=x6 B. (x2)4=x6 C. x3+x3=2x6 D. (−2x)3=−6x3
2. 在以下关于体育运动的图标中，是轴对称图形的是(    )
A. B. C. D.
3. 下列事件是必然事件的是(    )
A. 掷一枚质地均匀的骰子，掷出的点数是偶数
B. 两条线段可以组成一个三角形
C. 400人中至少有两个人的生日在同一天
D. 车辆随机到达一个路口，遇到绿灯
4. 如图，把一个直角三角尺的直角顶点放在直尺的一边上，若∠1=50°，则∠2=(    )



A. 20°
B. 30°
C. 40°
D. 50°
5. 如图，把两根木条AB和AC的一端A用螺栓固定在一起，木条AC自由转动至AC′位置．在转动过程中，下面的量是常量的为(    )


A. ∠BAC的度数 B. BC的长度 C. △ABC的面积 D. AC的长度
6. 如图，点O在直线AB上，OC⊥OD，若∠BOD=26°，则∠AOC的补角的大小为(    )
A. 26°
B. 64°
C. 116°
D. 154°
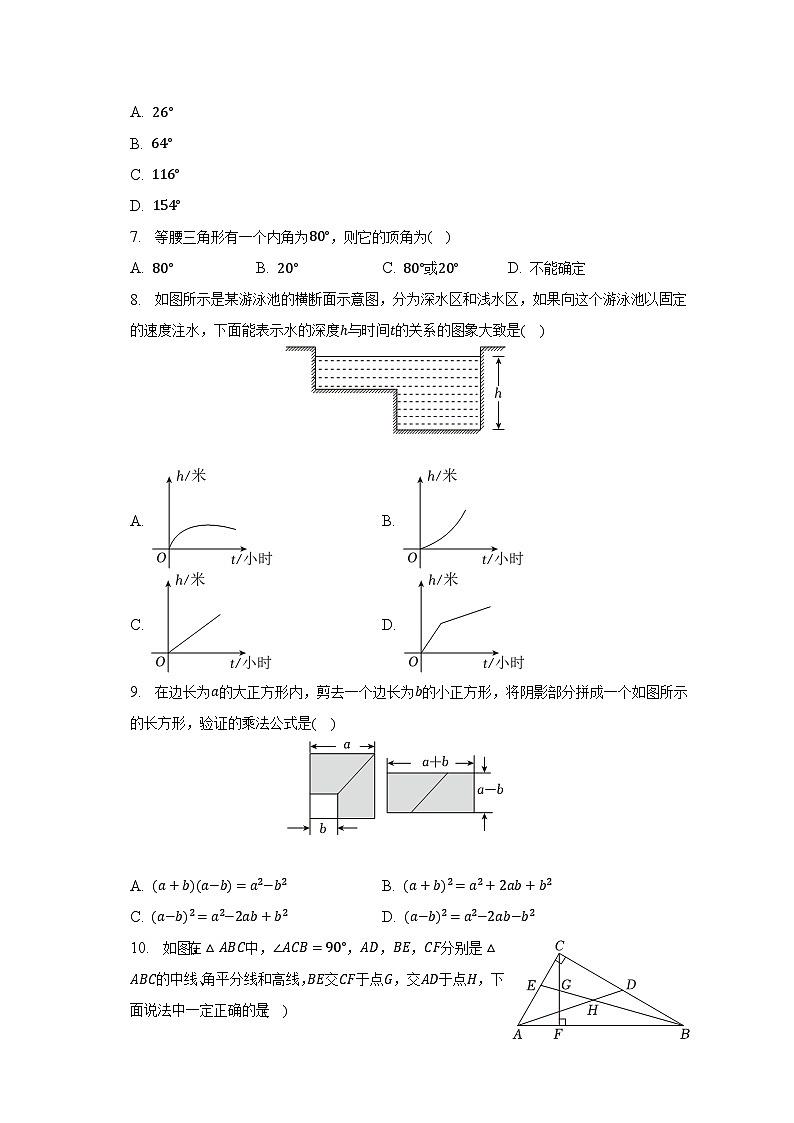
7. 等腰三角形有一个内角为80°，则它的顶角为(    )
A. 80° B. 20° C. 80°或20° D. 不能确定
8. 如图所示是某游泳池的横断面示意图，分为深水区和浅水区，如果向这个游泳池以固定的速度注水，下面能表示水的深度h与时间t的关系的图象大致是(    )

A. B.
C. D.
9. 在边长为a的大正方形内，剪去一个边长为b的小正方形，将阴影部分拼成一个如图所示的长方形，验证的乘法公式是(    )

A. (a+b)(a−b)=a2−b2 B. (a+b)2=a2+2ab+b2
C. (a−b)2=a2−2ab+b2 D. (a−b)2=a2−2ab−b2
10. 如图，在△ABC中，∠ACB=90°，AD，BE，CF分别是△ABC的中线、角平分线和高线，BE交CF于点G，交AD于点H，下面说法中一定正确的是(    )
①△ACD的面积等于△ABD的面积；
②∠CEG=∠CGE；
③∠ACF=2∠ABE；
④AH=BH．
A. ①②③④ B. ①②③ C. ②④ D. ①③
二、填空题（本大题共6小题，共18.0分）
11. 将0.0000025用科学记数法表示为______．
12. 转动如图所示的转盘，转盘停止后，指针落在白色区域的概率是______ ．


13. 如图，体育课上，老师测量学生跳远成绩选取的是AB的长度，其依据是______．

14. 长方形的周长为20cm，其中一边为x cm(其中x>0)，另一边为y cm，则y关于x的关系式为______．
15. 如图，在△ABC中，∠A=58°，∠ACB的平分线交AB于点D，分别以点B，C为圆心，大于12C的长为半径作弧，两弧交于点E，F，过点E，F的直线交AB于点G，若∠DCG=10°，则∠B的度数是______ ．

16. 如图，在锐角△ABC中，∠ABC=30°，AC=5，△ABC的面积为23，P为△ABC内部一点，分别作点P关于AB，BC，AC的对称点P1，P2，P3，连接PP1，PP2，PP3，P1P2，则2P1P2+PP3的最小值为______ ．

三、解答题（本大题共9小题，共82.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题6.0分)
计算：−12024−|−5|+(2023−π)0+(13)−1．
18. (本小题8.0分)
先化简，再求值：[(2a+b)2−2a(a−b)+(a−b)(a+b)]÷(3a)，其中a=−13,b=1．
19. (本小题8.0分)
如图，在四边形ABCD中，AD//BC，∠A=120°．
(1)用直尺和圆规作∠ABC的角平分线BE，交AD于点E(保留作图痕迹，不写作法)；
(2)求∠AEB的度数(补全下列推理过程)．
解：∵AD//BC(已知)
∴∠A+∠ABC=180°(______ )
∵∠A=120°(已知)
∴∠ABC=180°−∠A=60°
∵BE平分∠ABC(已知)
∴∠EBC=12 ______ =30°(角平分线的定义)
∵AD//BC(已知)
∴∠AEB=∠EBC= ______ °(______ )

20. (本小题8.0分)
任意掷一枚质地均匀的骰子．
(1)掷出的点数是4的概率是______ ；
(2)掷出的点数是7的概率是______ ；
(3)掷出的点数是偶数的概率是多少？
21. (本小题8.0分)
在所给网格图中，每小格都是边长为1的正方形，每个小正方形的顶点都称为“格点”，△ABC的顶点都在格点上．
(1)在图1中，作出△ABC关于直线l成轴对称的图形Δ A1B1C1；
(2)在图2的直线l上画出点P，使△PBC的周长最小(保留作图痕迹，并标上字母P)；
(3)在图3的直线l上画出点Q，使|QC−QB|值最大(保留作图痕迹，并标上字母Q)；
(4)△ABC的面积是______ ．


22. (本小题10.0分)
如图，AB⊥AC于点A，BD⊥CD于点D，AC与DB相交于点O，BO=CO．
(1)求证：AB=DC；
(2)若AC=5，∠ABD=26°，则BD= ______ ，∠DBC= ______ °.

23. (本小题10.0分)
甲、乙两个长方形，其边长如图所示(m>0)，其面积分别为S1，S2．
(1)用含m的代数式表示：S1= ______ ，S2= ______ ；(结果化为最简形式)
(2)用“<”“>”或“=”填空：S1 ______ S2；
(3)若一个正方形的周长等于甲、乙两个长方形的周长之和，设该正方形的面积为S3，试探究：S3与2(S1+S2)的差是否为定值？若为定值，请求出该值；如果不是，请说明理由．


24. (本小题12.0分)
如图1，在长方形ABCD中，AB=CD=8cm，AD=BC=10cm，点P从点A出发，沿A→B→C→D的路线运动，到点D停止；点Q从点D出发，沿D→C→B→A的路线运动，到点A停止.若点P，Q同时出发，点P的速度为1cm/s，点Q的速度为3cm/s，运动a秒后，点P，Q同时改变速度，点P的速度变为b cm/s，点Q的速度变为d cm/s，直到停止.图2是点P出发x秒后，△APD的面积S1(cm2)与运动时间x(秒)的关系图象；图3是点Q出发x秒后，△AQD的面积S2(cm2)与运动时间x(秒)的关系图象．
(1)根据图象得：a= ______ 秒，b= ______ cm/s，c= ______ 秒，d= ______ cm/s；
(2)设点P已行的路程为y1(cm)，点Q还剩的路程为y2(cm)，当x>a时，请分别求出y1、y2和运动时间x(s)的关系式；
(3)当x= ______ 时，△PBQ为等腰三角形．


25. (本小题12.0分)
在△ABC中，∠BAC=α，AB=AC，过点A作∠EAF=12α(使点E，A，F按顺时针的顺序排列)，过点C作直线CM⊥直线AE，垂足为点M，直线CM交直线AF于点N，连接BN．
(1)如图1，若α=90°，∠EAF的边都在∠BAC的内部，作点C关于AE的对称点C′．
①∠CAE+∠BAF= ______ °，BN ______ C′N；(填“<”“>”或“=”)
②求证：MN=CM+BN．
(2)如图2，若α=130°，∠EAF的边都在∠BAC的外部，当AM=4，MN=411BN，△ACN的面积为12时，请直接写出CM的长；
(3)若90°<α<180°，∠EAF有一条边在∠BAC的内部，请直接写出线段MN，BN，CN之间的等量关系．


答案和解析

1.【答案】A 
【解析】解：A、x2⋅x4=x6，故A符合题意；
B、(x2)4=x8，故B不符合题意；
C、x3+x3=2x3，故C不符合题意；
D、(−2x)3=−8x3，故D不符合题意；
故选：A．
利用合并同类项的法则，同底数幂的乘法的法则，幂的乘方与积的乘方的法则对各项进行运算即可．
本题主要考查幂的乘方与积的乘方，同底数幂的乘法，合并同类项，解答的关键是对相应的运算法则的掌握．

2.【答案】D 
【解析】解：A、图标不属于轴对称图形，故此选项不符合题意；
B、图标不属于轴对称图形，故此选项不符合题意；
C、图标不属于轴对称图形，故此选项不符合题意；
D、图标属于轴对称图形，故此选项符合题意．
故选：D．
根据轴对称图形的概念判断即可．
本题考查的是轴对称图形的概念，如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．

3.【答案】C 
【解析】解：A、掷一枚质地均匀的骰子，掷出的点数是偶数，是随机事件，不符合题意；
B、两条线段可以组成一个三角形，是不可能事件，不符合题意；
C、400人中至少有两个人的生日在同一天，是必然事件，符合题意；
D、车辆随机到达一个路口，遇到绿灯，是随机事件，不符合题意；
故选：C．
根据事件发生的可能性大小判断．
本题考查的是必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．

4.【答案】C 
【解析】
【分析】
根据两直线平行，同位角相等可得∠3=∠1，再根据平角等于180°列式计算即可得解．
本题考查了平行线的性质，平角的定义，熟记性质并准确识图是解题的关键．
【解答】
解：∵直尺对边互相平行，
∴∠3=∠1=50°，
∴∠2=180°−50°−90°=40°．
故选：C．  
5.【答案】D 
【解析】解：木条AC绕点A自由转动至AC′过程中，AC的长度始终不变，
故AC的长度是常量；
而∠BAC的度数、BC的长度、△ABC的面积一直在变化，均是变量．
故选：D．
根据常量和变量的定义进行判断．
本题考查常量和变量，理解题意，确定变与不变是求解本题的关键．

6.【答案】C 
【解析】解：∵OC⊥OD，
∴∠COD=90°，
∵∠BOD=26°，
∴∠COB=∠COD−∠BOD=64°，
∴∠AOC=180°−∠COB=116°，
故选：C．
根据垂直定义可得∠COD=90°，从而利用角的和差关系可得∠COB=64°，然后利用邻补角的定义，进行计算即可解答．
本题考查了垂线以及余角和补角，根据题目的已知条件并结合图形进行分析是解题的关键．

7.【答案】C 
【解析】解：①80°角是顶角时，三角形的顶角为80°，
②80°角是底角时，顶角为180°−80°×2=20°，
综上所述，该等腰三角形顶角的度数为80°或20°．
故选C．
分80°角是顶角与底角两种情况讨论求解．
本题考查了等腰三角形两底角相等的性质，难点在于要分情况讨论求解．

8.【答案】D 
【解析】解：根据题意和图形的形状，可知水的最大深度h与时间t之间的关系分为两段，先快后慢．
故选：D．
首先看图可知，蓄水池的下部分比上部分的体积小，故h与t的关系变化为先快后慢．
本题考查根据几何图形的性质，确定函数的图象和函数图象的作图能力．要能根据几何图形和图形上的数据分析得出所对应的函数的类型和所需要的条件，结合实际意义画出正确的图象．

9.【答案】A 
【解析】解：左图中阴影部分可以看作两个正方形的面积差，即a2−b2，右图的长为(a+b)，宽为(a−b)的长方形，因此面积为(a+b)(a−b)，
所以有a2−b2=(a+b)(a−b)，
即(a+b)(a−b)=a2−b2，
故选：A．
用代数式表示两个图形中阴影部分的面积即可．
本题考查平方差公式，掌握平方差公式的结构特征是正确解答的前提，用代数式表示两个图形中阴影部分的面积是解决问题的关键．

10.【答案】B 
【解析】解：∵AD是△ABC的中线，
∴CD=BD，
而点A到BC的距离相等，
∴△ACD的面积等于△ABD的面积，
故①正确；
∵BE是△ABC的角平分线，
∴∠ABE=∠CBE，
∵CF是△ABC的高线，
∴∠CFA=90°，
∴∠CAB+∠ACF=90°，
∵∠ACB=90°，
∴∠ACF+∠BCG=90°，
∴∠CAB=∠BCG，
∵∠CEG是△ABE的一个外角，
∴∠CEG=∠CAB+∠ABE，
∵∠CGE是△BCG的一个外角，
∴∠CGE=∠CBE+∠BCG，
∴∠CEG=∠CGE，
故②正确；
∵CF是△ABC的高线，
∴∠CFB=90°，
∴∠CBF+∠BCF=90°，
∵∠ACB=90°，
∴∠ACF+∠BCF=90°，
∴∠ACF=∠CBF，
∵BE是△ABC的角平分线，
∴∠CBF=2∠ABE，
∴∠ACF=2∠ABE，
故③正确；
无法证得AH=BH，故④错误．
故正确的有①②③，
故选：B．
①根据等底同高即可判断△ACD的面积等于△ABD的面积；
②先根据同角的余角相等证得∠CAB=∠BCG，再根据角平分线的定义得出∠ABE=∠CBE，最后根据三角形外角的性质得出∠CEG=∠CAB+∠ABE，∠CGE=∠CBE+∠BCG，即可得证；
③先根据同角的余角相等证得∠ACF=∠CBF，再根据角平分线的定义得出∠CBF=2∠ABE，于是推出∠ACF=2∠ABE；
④无法证得AH=BH．
本题考查了三角形的面积，三角形外角的性质，同角的余角相等，角平分线的定义，熟练掌握这些性质是解题的关键．

11.【答案】2.5×10−6 
【解析】解：0.0000025=2.5×10−6，
故答案为：2.5×10−6．
绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10−n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
本题考查用科学记数法表示较小的数，一般形式为a×10−n，其中1≤|a|<10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．

12.【答案】34 
【解析】解：观察图形知：白色区域的圆心角为360°−90°=270°，
所以指针落在白色区域的概率是270360=34，
故答案为：34．
用白色区域圆心角的度数除以周角的度数即可求得答案．
本题考查了几何概率的知识，解题的关键是确定白色区域的圆心角的度数，难度中等．

13.【答案】垂线段最短 
【解析】解：测量运动员跳远成绩选取的是AB的长度，其依据是：垂线段最短．
故答案为：垂线段最短．
垂线段的性质：垂线段最短．利用垂线段的性质求解．
本题考查了垂线段的性质：垂线段最短．实际问题中涉及线路最短问题时，其理论依据应从“两点之间，线段最短”和“垂线段最短”这两个中去选择．

14.【答案】y=10−x． 
【解析】解：由长方形的周长公式可得，2(x+y)=20，
即y=10−x，
故答案为：y=10−x．
根据长方形的周长公式可得答案．
本题考查函数关系式，掌握长方形的周长计算方法是得出正确答案的前提．

15.【答案】34° 
【解析】解：设∠B=α，根据作图可知EF是BC的垂直平分线，
∴GB=GC，
∴∠GCB=∠B=α，
∵CD是∠ACB的平分线，
∴∠ACD=∠BCD，
∵∠A=58°，∠DCG=10°，
∴∠ACB=2∠DCB=2(∠GCB+∠DCG)=2(α+10°)，
∵∠A+∠ACB+∠B=180°，∠A=58°，
∴58°+2(α+10)°+α=180°，
解得α=34°，
∴∠B=34°．
故答案为：34°．
设∠B=α，根据作图可知EF是BC的垂直平分线，可得GB=GC，根据等边对等角可得∠GCB=∠B=α，根据角平分线的意义可得∠ACD=∠BCD，结合已知条件，根据三角形内角和定理列出方程，解方程即可求解．
本题考查了作线段的垂直平分线，线段的垂直平分线的性质，等边对等角，三角形内角和定理，掌握基本作图是解题的关键．

16.【答案】925 
【解析】解：设PP3与AC交于点Q，则PQ=12PP3，连接BP、BQ、BP1、BP2，作BM⊥AC，垂足为M，
∵AC=5，△ABC的面积为23，
∴BM=465，
根据对称性得BP=BP1=BP2，∠ABP=∠ABP1，∠CBP=∠CBP2，
∴∠P1BP2=2∠ABC=60°，
∴△P1BP2是正三角形，
∴P1P2=BP1=BP，
∴2P1P2+PP3=2(P1P2+12PP3)=2(BP+PQ)≥2BQ≥2BM=925，
故答案为：925．
由∠ABC=30°和对称想到构造正三角形，将P1P2转化成BP，将2P1P2+PP3提取系数2，最终转化成垂线段最短．
本题考查了轴对称、正三角形、三角形面积、垂线段最短等知识，关键是将P1P2转化成BP，将2P1P2+PP3提取系数2，最终转化成垂线段最短．形式上易与胡不归混淆．

17.【答案】解：原式=−1−5+1+3
=−2． 
【解析】直接利用有理数的乘方运算法则、绝对值的性质、零指数幂的性质、负整数指数幂的性质分别化简，进而得出答案．
此题主要考查了实数的运算，正确化简各数是解题关键．

18.【答案】解：[(2a+b)2−2a(a−b)+(a−b)(a+b)]÷(3a)
=(4a2+4ab+b2−2a2+2ab+a2−b2)÷(3a)
=(3a2+6ab)÷(3a)
=a+2b，
当a=−13,b=1时，原式=−13+2×1
=−13+2
=53． 
【解析】先利用平方差公式，完全平方公式，单项式乘多项式计算括号里，再算括号外，然后把a，b的值代入化简后的式子进行计算即可解答．
本题考查了整式的混合运算−化简求值，准确熟练地进行计算是解题的关键．

19.【答案】两直线平行，同旁内角互补  ∠ABC  30  两直线平行，内错角相等 
【解析】解：(1)如图：BE即为所求；
(2)∵AD//BC(已知)，
∴∠A+∠ABC=180°(两直线平行，同旁内角互补)，
∵∠A=120°(已知)，
∴∠ABC=180°−∠A=60°，
∵BE平分∠ABC(已知)，
∴∠EBC=12∠ABC=30°(角平分线的定义)，
∵AD//BC(已知)，
∴∠AEB=∠EBC=30°(两直线平行，内错角相等)，
故答案为：两直线平行，同旁内角互补；∠ABC；30；两直线平行，内错角相等．
(1)根据作角平分线的基本作法作图；
(2)根据平行线的选择求解．
本题考查了复杂作图，掌握平行线的性质是解题的关键．

20.【答案】16  0 
【解析】解：(1)∵6个面上只有1个面上的点数是4，
∴掷出的点数是4的概率是16，
故答案为：16；
(2)∵6个面上没有数字7，
∴掷出的点数是7的概率是0，
故答案为：0；
(3)∵6个面上有2，4，6三个偶数，
∴掷出的点数是偶数的概率是36=12．
根据概率的意义即可得解．
本题考查了概率公式的知识，解题的关键是了解概率的求法，难度不大．

21.【答案】5.5 
【解析】解：(1)如图1中，ΔA1B1C1即为所求；
(2)如图2中，点P即为所求；
(3)如图3中，点Q即为所求；
(4)△ABC的面积=3×5−12×2×3−12×1×3−12×2×5=5.5．
故答案为：5.5．

(1)利用轴对称变换的性质分别作出A，B，C的对应点A1，B1，C1即可；
(2)连接BC1交直线l于点P，连接PC，点P即为所求；
(3)延长BC交直线l于点QW，点Q即为所求；
(4)表三角形的面积看成矩形的面积减去周围的三个三角形面积即可．
本题考查作图−轴对称变换，轴对称最短问题等知识，解题的关键是理解题意，灵活运用所学知识解决问题．

22.【答案】5  32 
【解析】(1)证明：∵AB⊥AC于点A，BD⊥CD于点D，
∴∠A=∠D=90°，
∵AC与DB相交于点O，BO=CO，
∴∠ACB=∠DBC，
在△ABC和△DCB中，
∠A=∠D∠ACB=∠DBCBC=CB，
∴△ABC≌△DCB(AAS)，
∴AB=DC．
(2)解：∵△ABC≌△DCB，
∴AC=BD，
∴AC=5，
∴BD=5，
∵∠A=90°，∠ABD=26°，
∴∠AOB=90°−∠ABD=90°−26°=64°，
∴∠ACB+∠DBC=∠AOB=64°，
∵∠ACB=∠DBC，
∴∠DBC+∠DBC=64°，
∴∠DBC=32°，
故答案为：5，32．
(1)由AB⊥AC于点A，BD⊥CD于点D，得∠A=∠D=90°，由BO=CO，得∠ACB=∠DBC，而BC=CB，即可根据全等三角形的判定定理“AAS”证明△ABC≌△DCB，得AB=DC；
(2)由△ABC≌△DCB，得AC=BD=5，由∠A=90°，∠ABD=26°，得∠AOB=64°，则∠ACB+∠DBC=∠AOB=64°，而∠ACB=∠DBC，则∠DBC=32°，于是得到问题的答案．
此题重点考查全等三角形的判定与性质、“等边对等角”、直角三角形的两个锐角互余、三角形的一个外角等于与它不相邻的两个内角的和等知识，证明△ABC≌△DCB是解题的关键．

23.【答案】m2+6m+5  m2+6m+8  < 
【解析】解：(1)根据长方形的面积公式可得：S1=(m+5)(m+1)=m2+6m+5，
S2=(m+4)(m+2)=m2+6m+8，
故答案为：m2+6m+5；m2+6m+8；
(2)S1−S2=m2+6m+5−(m2+6m+8)
=m2+6m+5−m2−6m−8
=−3<0，
故S1 故答案为：<；
(3)正方形的周长为：C=2×(m+5+m+1+m+4+m+2)=8m+24，
∴正方形的边长为：C÷4=(8m+24)÷4=2m+6，
∴S3=(2m+6)⋅(2m+6)=4m2+24m+36，
∴S3−2(S1+S2)=4m2+24m+36−2×(m2+6m+5+m2+6m+8)
=4m2+24m+36−2×(2m2+12m+13)
=10，
故S3与2(S1+S2)的差是定值，定值为10．
(1)根据长方形的面积公式进行求解；
(2)利用S1−S2进行比较大小；
(3)结合(1)列出式子S3−2(S1+S2)，进行判断．
本题考查了多项式乘多项式，掌握多项式乘多项式的方法是关键．

24.【答案】6  4  11  1 85或5或667 
【解析】解：(1)点P从A→B，
S1=12⋅AD⋅AP=12×10×x=5x，
  点P从B→C，
S1=12⋅AD⋅AB=12×10×8=40，
由图2，30<40，
∴点P在A→B上运动
∴S1=5x=30，
x=6，
即a=6，
点Q从D→C，
S₂=12⋅AD⋅DQ=12×10×3x=15x，
3x≤10，x≤103，
点Q从C→B，
S₂=12⋅AD⋅CD=12×10×8=40，
点P从6s到6.5s，
即8−6=2(cm)，
S=40−30=5×10×(6.5−6)b，
∴b=4，
(8+10)÷4=4.5，
∴c=6.5+4.5=11，
当a=6时，
Q的路程为3×6=18
即Q从D→C→B
由图3，共用14秒，
则Q从B→A，
d=AB=1，
(2)当x>a时，
即x>6，
y1=6+4(x−6)=4x−18，
∴y1=4x−18(6 y2=8−(x−6)=14−x，
∴y2=14−x(6 (3)△PBQ为等腰三角形，
①当点P在AB上，点Q在DC上运动时，
过点Q向AB作垂线交于点E，如图，

由图可知，BE=CQ，
即8−x2=8−3x，
解得x=85(符合题意)；
②当点P在AB上，点Q在CB上运动时，
连接PQ，如图，

BP=BQ，
8−x=18−3x，
解得x=5(符合题意)；
③当点P在BC上，点Q在AB上运动时，
不合题意舍去；
④当点P在CD上，点Q在AB上运动时，
BE=CP，
6+4(x−6)−18=x−62，
解得x=667(符合题意)；

故故答案为：85或5或667．
(1)当P在AB上运动时表示出S1，并求出a，根据图则面积之差40−30，进而求出b，此时点Q运动到点B求出d，
(2)根据路程等于速度×时间作答，
(3)分情况讨论，当点P在AB上，点Q在DC上；当点P在AB上，点Q在CB上；当点P在BC上，点Q在AB上；当点P在CD上，点Q在AB上，四种情况进行讨论．
本题考查四边形等腰三角形等的综合题，解题的关键是对图形的熟练掌握和对不同情况的分类讨论．

25.【答案】45  = 
【解析】(1)①解：如图1，

连接AC′，
∵∠EAF=12∠BAC=12×90°=45°，
∴∠CAE+∠BAF=∠BAC−∠EAF=90°−45°=45，
∵点C和点C′关于AE对称，
∴AC=AC′，∠CAM=∠MAC′，
∴∠MAC′+∠BAF=45°，
∵AB=AC，
∴AB=AC′，
∵∠MAC′+∠NAC′=45°，
∴∠BAF=∠NAC′=45°，
∴△BAN≌△C′AN(SAS)，
∴BN=C′N，
故答案为：45，=；
②证明：∵点C和点C′关于AE对称，
∴CM=C′M，
由①得：BN=C′N，
∴MN=C′M+C′N=CM+BN；
(2)解：如图2，

作点C关于AE的对称点D，连接AD，
∴AD=AC，∠DAM=∠CAM=∠CAF+∠EAF，
∵∠EAF=12∠BCA=65°，
∴∠DAM=∠CAF+65°，
∴∠DAN=∠ADM+∠EAF=130°+∠CAF，
∵∠BAN=∠BAC+∠CAF=130°+∠CAF，
∴∠BAN=∠DAN，
∵AN=AN，
∴△ADN≌△BAN(SAS)，
∴DN=BN，
∴DM+MN=BN，
∴CM+MN=BN，
∵MN=411BN，
∴可设BN=11k，MN=4k，
∵S△ACN=12CN⋅AM=12，
∴4CN=24，
∴CN=6，
∴CM=CN+MN=6+4k，
∴6+4k+4k=11k，
∴k=2，
∴CM=6+4×2=14；
(3)解：如图3，

当AF在∠BAC的内部时，
作点C关于AE的对称点D，
∴CM=DM，
同理(2)得：△ADN≌△ABN，
∴BN=DN，
∴BN=MN+DM=MN+CM，

当AE在∠BAC的内部时，
作点C关于AE的对称点D，
同理可得：△ABN≌△ADN，
∴AN=DN=MN+DM=MN+CM，
综上所述：BN=MN+CM．
(1)连接AC′，可证明△BAN≌△C′AN，进一步得出结论；
(2)作点C关于AE的对称点D，连接AD，可证得△ADN≌△BAN，从而得出DN=BN，进而得出CM+MN=BN，可设BN=11k，MN=4k，先求出CN=6，从而表示出CM=CN+MN=6+4k，进而列出6+4k+4k=11k，求得k的值，进一步得出结果；
(3)当AF在∠BAC的内部时，作点C关于AE的对称点D，可证得△ADN≌△ABN，从而得出BN=DN，从而BN=MN+DM=MN+CM；
当AE在∠BAC的内部时，作点C关于AE的对称点D，同样得出结论．
本题考查了轴对称的性质，全等三角形的判定和性质等知识，解决问题的关键是作辅助线，构造全等三角形．