数学21.1 一元二次方程说课ppt课件

这是一份数学21.1 一元二次方程说课ppt课件，共18页。PPT课件主要包含了学习目标，自学指导，x11－x，整理得，自学检测，二次项，一次项，常数项，二次项系数，一次项系数等内容，欢迎下载使用。
1、了解一元二次方程概念的形成过程， 知道什么是一元二次方程； 2、会把一元二次方程化为一般形式， 并知道各项及系数的名称.
请认真看课本P2页--P3页“例题”之前的全部的内容. 看懂问题1、2的简答过程，要求： 1、看懂问题1,2的解答过程.试回答“云图”中的问题， 方程①②③有什么共同点？ 2、理解并熟记一元二次方程的定义； 一元二次方程的一般形式为: ; 为什么规定a≠0? 3、能判断一个数是不是一元二次方程的解（根）， 6分钟后比谁又快又准回答以上问题
1. 用 22 cm长的铁丝，折成一个面积为 30 cm2的矩形，求这个矩形的长与宽.
设矩形的长为 x cm，
则宽为（11－x ） cm ，
x2 － 11x + 30 = 0
根据矩形的面积为30 cm2，得
x2 ＋ 2x = 255
x2 ＋ 2x－ 4= 0
x2 － 75x＋ 350 = 0
这些方程有什么共同点？
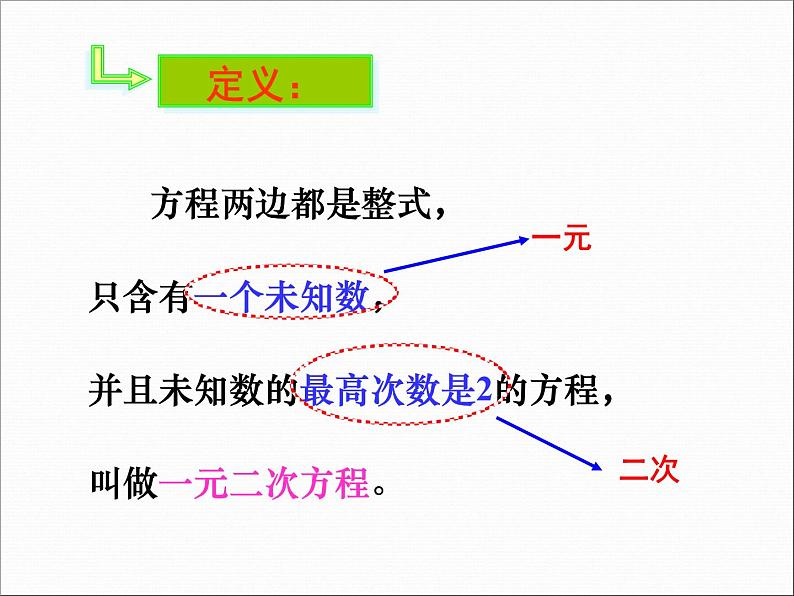
方程两边都是整式。
方程中只含有一个未知数。
未知数的最高次数是2。
方程两边都是整式，只含有一个未知数，并且未知数的最高次数是2的方程，叫做一元二次方程。
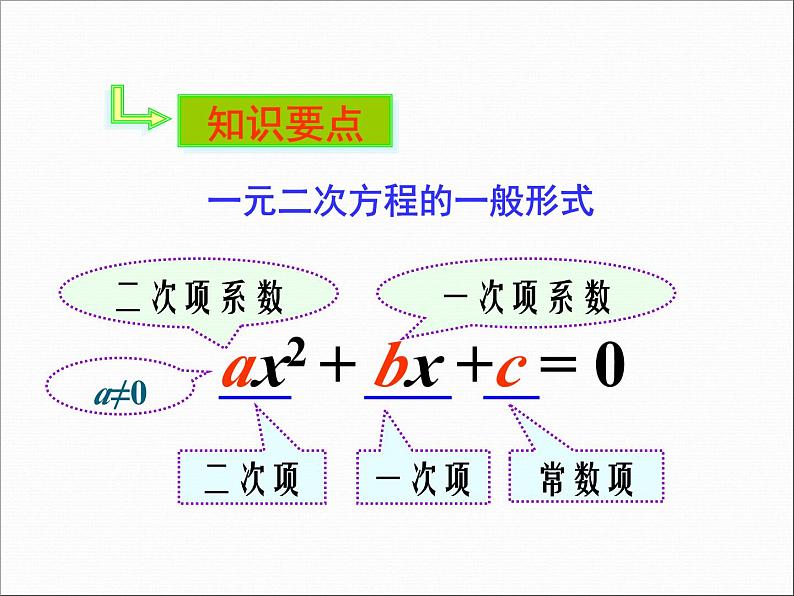
ax2 + bx +c = 0
一元二次方程的一般形式
当 a = 0 时，方程变为 bx＋c = 0 ，不再是一元二次方程。
为什么要限制a≠0，b、c 可以为零吗？
下列哪些是一元二次方程？
判断一个方程是否为一元二次方程，不能只看表面，能化简时应先化简。
方程 x2 － x = 0
满足2x2 － 2x = 0
x = 0，x = 1 都是方程 2x2 － 2x =0 的解。
也满足2x2 － 2x = 0
使一元二次方程左右两边相等的未知数的值，就是一元二次方程的解。
判断下列哪些是方程 的根？
0，2，4，6，8，-2，-4，-6，-8.
x2+6x-16=0
只含有一个未知数，并且未知数的最高次数是 2的整式方程叫做一元二次方程。
1.一元二次方程的概念：
2.一元二次方程的一般形式:
一般地，任何一个关于 x 的一元二次方程都可以化为 （a，b，c为常数，a≠0）的形式，称为一元二次方程的一般形式。
也叫做一元二次方程的根。
3. 一元二次方程的解：
1. 将下列方程化为一元二次方程的一般形式，并写出其中的二次项系数、一次项系数及常数项。
2. 下面哪些数是方程 的根？ －4，－3，－2，－1，0，1，2，3，4．
解：将上面的这些数代入后， 只有－2和－3满足方程的等式，
所以 x =－2或 x =－3是一元二次方程的两根。
3. 长 5 m的梯子斜靠在墙上，梯子的底端与墙的距离是3 m。若梯子底端向左滑动的距离与梯子顶端向下滑动的距离相等，求梯子滑动的距离。