高中数学人教A版 (2019)必修 第一册4.2 指数函数教案设计

这是一份高中数学人教A版 (2019)必修 第一册4.2 指数函数教案设计，共5页。教案主要包含了创设情境，概念形成，实践操作，习题讲练，课堂小结，课后作业等内容，欢迎下载使用。
2.1.2《指数函数及其性质》（第1课时）                             杨仙逸中学   陈红霞   2019年9月教学目标：   理解指数函数的概念和意义，能画出具体指数函数的图象。   初步掌握指数函数的性质，并能解决与指数函数有关的定义域、值域、定点问题，培养逻辑推理核心素养。教学重点：指数函数的概念和性质；底数a对函数的影响.教学难点：用数形结合方法从具体到一般的探索、概括指数函数的性质；底数a对函数的影响.教学设计：讲授法与讨论法相结合；探究学习与合作学习相结合教具准备：触控一体机、白板课件、白纸、剪刀、绳子教学过程：一、创设情境、引入问题（多媒体显示引例，学生阅读引例，尝试得出函数式子，师生共同分析引例验证结论）引例1：：把一张纸不断翻折，可以折多少次？折30次后纸的厚度有多高？如果第x次翻折得到的纸厚度是原来纸张厚度的y倍，那么y与x的关系式子是什么？引例2：：庄子曰：一尺之棰，日取其半。这是什么意思？我们手上没有棍子，我用一根绳子代替，把一条绳子不断对折剪掉一半，可以剪多少次？有没有同学愿意试试？如果第x次剪掉一半得到的绳子长度是原来绳子长度的y倍，那么y与x的关系式子是什么？问题：（引导学生思考，回答问题）        ①这个式子中两个变量是否具有函数关系？ ②这类函数是我们学过的某一类函数吗？   （这就是我今天为大家带来的“知识”礼物：指数函数及其性质） （板书课题） ,          ③仔细观察，这两个函数式子有什么共性？（均是幂的形式；底数是常数；指数是自变量）  （师：如果用字母代替其中的底数，那么上述两式就可以表示成的形式—多媒体显示结论）二、概念形成、探究特征1、指数函数的概念:  一般地，函数且叫做指数函数，其中是自变量，函数的定义域是R        （按a分成：①；②）（板书）2、思考：（1）为什么指数函数对底数a有范围要求？即且？（那么与的   情况又是怎样的呢？引导学生共同分析）    ①当时, 不一定有意义，例如（负数没有偶次方根）    ②当时，若时，恒等于；若时，无意义；所以，当时，不一定有意义.    ③当恒等于1，是我们之前研究过的常函数，没有再研究的价值.    所以，这三种情况不利于我们研究指数函数，因此规定：且.（从上面的分析中，让我们知道，理解数学概念不能只停留在表面上，还应该深度透视）（2）指数函数的特点:  根据定义, 具备什么条件的函数是指数函数?再次观察：           ,  ①     底数都是 常数            ② 变量都在 指数 位置        ③ 前的系数都是1            ④ 自变量x的系数都是 1                ⑤ 自变量x的指数都是1   归纳：①底数a为常数，且；②指数只含自变量x； ③前的系数为1（板书）    课堂活动---------小组竞赛，引用希沃白板课件里的活动功能设置游戏，让两位同学在白板上比赛。    深度透视：根据指数函数的定义，指出下列哪些函数是指数函数？（1）   （2）    （3）    （4）    （5）  （6）     （7）     （8）    归纳：（1）判断一个函数是不是指数函数, 要严格按照指数函数的定义形式来判断。指数    函数形式一定是“（且）”，任何与其形式不符的都不能称其为指数函数。      （在学习了指数函数基本概念之后，我们来探讨一下它的图象和性质又是怎样的呢？）三、实践操作、探求新知    1、画图：指数函数的图象      （1）动手画一画：在同一坐标系下，作出下列函数图象（分组画图：1、2组画①；3、4组画②）    ①，     ；             ②，    （强调的变化）   思考：（1）用什么方法可以得到指数函数的图象呢？都有哪些步骤？（描点法：列表、描    点、连线）   （2）在同一坐标系下，作出函数，，，的图象。   列出x、y的对应值表（强调：① x在原点附近取整数值；②描点后要用“光滑曲线”将这些点连          接起来）（教师示例其一，板演列表、描点、连线步骤） ……-3-2-10123…………1248……   借助希沃白板里的函数工具用多媒体演示分别在和时的若干个函数图象。2、观察并回答：   （1）观察当看它们有什么共同特征？（）  （2）观察当看它们有什么共同特征？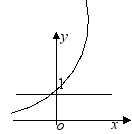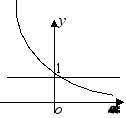（）  （提示： 从形状（一撇一捺），图象分布状况（图象都在x轴上方），图象刻画指标：定义域、恒过点、单调性（从左到右上升、下降）等方面看，引导分析得出一般图象）3、归纳特征：（1） 指数函数的图象特征：   ①向轴正负方向无限延伸；（定义域）②函数图象都在轴上方；（值域）   ③函数图象都经过(0,1)点；（恒过点） ④图象关于原点和轴不对称；（奇偶性）   ⑤从左向右看，当时图象逐渐上升；当时图象逐渐下降；（单调性）   ⑥图象分为两类： （Ⅰ）在第一象限内，图象的纵坐标都大于1；在第二象限内，图象的纵坐标都小于1   （Ⅱ）在第一象限内，图象的纵坐标都小于1；在第二象限内，图象的纵坐标都大于1      （2）指数函数的性质：（引导学生分析总结）       图 象  性   质（1）定义域：R（2）值域：（0，+∞）（3）恒过点，即时（4）奇偶性：非奇非偶函数（5）在R上是单调增函数（5）在R上是单调减函数（6）当 x > 0 时，y>1             
     当 x < 0 时 ，0< y<1 ;（6）当 x > 0 时，0< y<1                当 x < 0 时 ， y>1 ;四、习题讲练、巩固新知例1：已知指数函数的函数图象经过点， 求、、的值.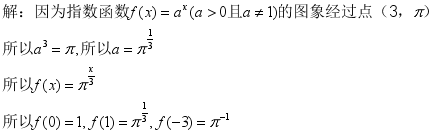 例2：比较下列各题中两个值的大小:（1）          （2）           五、课堂练习利用希沃白板里的《学科题库》功能，选择了三道习题让学生完成，学生完成后再用此功能展示答案进行评讲。   六、课堂小结1、知识：学习了指数函数的定义、指数函数的图象和性质。2、方法：学习了数形结合思想、待定系数法等数学思想。   结束语：本节课学习了指数函数后，在函数中又增加了一类新的成员，丰富了知识，开阔了视野，它必将在后续函数的学习和应用中发挥着重要作用。 七、课后作业：作业：习题2-1  A组第7、8题