必修 第一册3.2 基本不等式优秀ppt课件

这是一份必修 第一册3.2 基本不等式优秀ppt课件，共25页。PPT课件主要包含了复习回顾，不等式的基本性质，问题情境，数学建构，数学探究，基本不等式，两个重要不等式，数学应用，变式拓展，数学练习等内容，欢迎下载使用。

2、下图是在北京召开的第24界国际数学家大会会标，会 标是根据中国古代数学家赵爽的弦图设计的，颜色的 明暗使它看上去象一个风车，代表中国人民热情好客， 你能在这个图案中找出一些相等关系或不等关系吗？
1、阅读教材第51页，了解“算数平均数”与“几何平均 数”的概念，并思考算数平均数与几何平均数又怎样 的大小关系？
1、算术平均数与几何平均数的概念
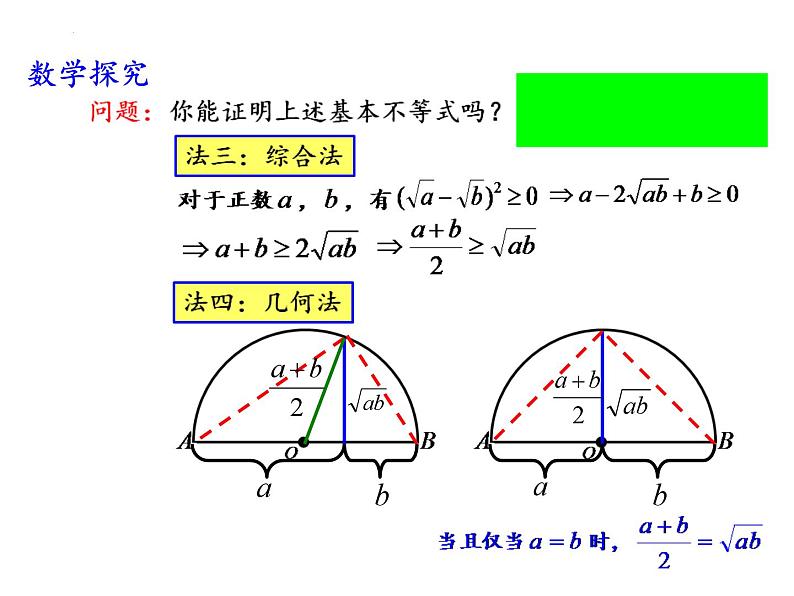
说明：(1)当a ≥0，b ≥0时，上述不等式仍然成立；
(3)当a =0或b =0时，不等式虽成立，但不是经常研究 (无研究的意义)，故我们对基本不等式中a、b 的要 求主要是正数。
3、基本不等式应用的前提条件
一般地，当a、b∈R时，
5、基本不等式的推广(了解即可)
例1、证明不等式 a2＋b2 ≥2ab(a，b∈R)。
类型一 常见推论的证明
小结：作差法与不等式性质是证明中常用的方法。
已知a，b，c为任意的实数，求证：a2＋b2＋c2≥ab＋bc＋ca。
证明：∵a2＋b2≥2ab；b2＋c2≥2bc；c2＋a2≥2ca， ∴2(a2＋b2＋c2) ≥2(ab＋bc＋ca)， 即a2＋b2＋c2≥ab＋bc＋ca， 当且仅当a＝b＝c时，等号成立。
例2、设a，b为正数，证明下列不等式成立。
类型二 利用基本不等式证明不等式
利用基本不等式证明不等式的策略与注意事项：
(1)策略：从已证不等式和问题的已知条件出发，借助不 等式的性质和有关定理，经过逐步的逻辑推理， 最后转化为所求问题，其特征是以“已知”看“可 知”，逐步推向“未知”；
(2)注意事项： ①多次使用基本不等式时，要注意取得等号的条件是 否一致； ②累加法是不等式证明中的一种常用方法，证明不等 式时注意使用； ③对不能直接使用基本不等式的证明可重新组合，形 成基本不等式模型，再使用。
已知a，b，c都是正实数，求证：(a＋b)(b＋c)·(c＋a)≥8abc。
证明：∵a，b，c都是正实数， ∴a＋b≥2>0，b＋c≥2>0，c＋a≥2>0， ∴(a＋b)(b＋c)(c＋a)≥2·2·2＝8abc. 即(a＋b)(b＋c)(c＋a)≥8abc， 当且仅当a＝b＝c时，等号成立。
例4、某工厂生产某种产品，第一年产量为A，第二年的 增长率为 a，第三年的增长率为 b，这两年的平均 增长率为x (a，b，x均大于零)，则(　　)
类型三 利用基本不等式比较大小
2、在利用基本不等式证明的过程中，常需要把数、式 合理地拆成两项或多项或把恒等式变形配凑成适当 的数、式，以便于利用基本不等式。
1、已知a，b，c，d都是正实数， 求证：(ab＋cd)(ac＋bd) ≥ 4abcd。