初中数学4 平行线的性质教案

4　平行线的性质

1．经历探索平行线的性质定理的过程，获得证明的体验．

2．掌握平行线的性质定理，并能够应用平行线的性质定理解决一些问题．

重点： 理解和简单应用本节课中的三个定理．

难点： 运用公理、定理进行简单的推理，以及用几何语言进行表述．

一、导入新课

提出问题：

1．平行线的判定方法有哪三种？它们是先知道什么，后知道什么？

2．已知直线AB及其外一点P，画出过点P的AB的平行线．

3．根据同位角相等可以判定两直线平行，反过来如果两直线平行同位角之间有什么关系呢？内错角，同旁内角之间又有什么关系呢？

二、探究新知

探究1　我们已经知道：两直线平行，同位角相等．如何证明这个性质呢？

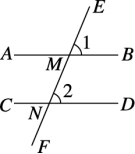
教材图7—8

同学们，我们证明定理的步骤是什么？

学生稍加回忆，就能回答：画图，根据图形写出已知、求证，并设法证明．

那么，平行线的这个性质的图形该怎么画，如何写已知、求证？

学生自主探究、交流讨论之后，可以得到：

已知：如教材图7－8所示，直线AB∥CD，∠1和∠2是直线AB被直线EF截出的同位角．

求证：∠1＝∠2.

该如何证明呢？今天介绍一个特别的方法——反证法．

证明：假设∠1≠∠2，那么我们可以过点M作直线GH，使∠EMH＝∠2.如教材图7－9所示．

根据“同位角相等，两直线平行”，可知GH∥CD.

又因为AB∥CD，这样经过点M存在两条直线AB与GH都与直线CD平行．

这与基本事实“过直线外一点有且只有一条直线与这条直线平行”相矛盾．

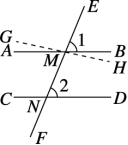
教材图7—9

这说明∠1≠∠2的假设不成立，所以∠1＝∠2.

由此，我们证明了以下的定理．

定理：两直线平行，同位角相等．

有时，直接证明很困难，我们就证明命题的另一面不成立．也就是假设结论的反面不成立，推导出与已知条件、定理、基本事实矛盾，那么假设不成立，原命题成立．

探究2　我们可以证明其他两条性质吗？

学生可以自己画出图形，写出已知、求证．

通过自主交流、同伴互助，学生基本可以口述定理证明的过程．教师规范地板书．

已知：如图，直线a∥b，∠4和∠2，∠2和∠3分别是直线a，b被直线c截出的内错角、同旁内角．

求证：∠1＝∠2，∠2＋∠3＝180°.

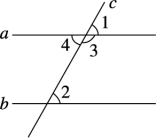
证明：∵a∥b(已知)，

∴∠1＝∠2(两直线平行，同位角相等)．

∵∠1＝∠4(对顶角相等)，

∴∠2＝∠4(等量代换)．

∵∠1＋∠3＝180°(邻补角定义)，

∴∠2＋∠3＝180°(等量代换)．

因此可以得到：

平行线的性质2：两条平行线被第三条直线所截，内错角相等．简单说成：两直线平行，内错角相等．

平行线的性质3：两条平行线被第三条直线所截，同旁内角互补．简单说成：两直线平行，同旁内角互补．

【思考】平行线的性质定理与判定定理在条件和结论方面有什么关系？

条件和结论的互换．平行线的性质定理是已知两直线平行，得到角的关系；而判定定理是已知角的关系，得到两直线平行．

探究3　如教材图7—11，b∥a，c∥a，∠1，∠2，∠3是直线a，b，c被直线d截出的同位角．

求证：b∥c.

想一想，要证明b∥c，也就是要证明什么，该如何证明？

学生自主探究、交流讨论，各小组派代表回答．其他小组补充．最后教师板书．

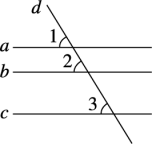
教材图7—11

证明：∵b∥a，c∥a，

∴∠1＝∠2，∠1＝∠3(两直线平行，同位角相等)，

∴∠2＝∠3(等量代换)，

∴b∥c(同位角相等，两直线平行)．

一般地，我们有如下定理：

平行于同一条直线的两条直线平行．

三、新知归纳

1．平行线的性质定理一：两直线平行，同位角相等．

2．平行线的性质定理二：两直线平行，内错角相等．

3．平行线的性质定理三：两直线平行，同旁内角互补．

4．平行线于同一条直线的两条直线平行．

四、典例剖析

例1　如图，已知AD∥BC，BD平分∠ABC，∠A∶∠ABC＝2∶1，求∠ADB的大小．

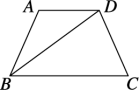
思路分析：利用AD∥BC，可以建立∠A与∠ABC之间的一种数量关系，利用∠A∶∠ABC＝2∶1，又可以建立它们的另一种数量关系，从而发现更多的已知角．

解：∵AD∥BC(已知)，∴∠A＋∠ABC＝180°(两直线平行，同旁内角互补)．又∵∠A∶∠ABC＝2∶1，∴∠ABC＝60°.∵BD平分∠ABC，∴∠DBC＝30°.∵AD∥BC，∴∠ADB＝∠DBC＝30°.(两直线平行，内错角相等)．

例2　如图，已知AB∥CD，∠ABE＝40°，∠CDE＝60°，求∠BED的大小．

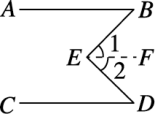
思路分析：平行线的性质共有3条，在实际解题时应根据实际情况灵活选择．另外，仔细分析已知条件获得更多结论是解题的关键

解：如图，过点E作EF∥AB(经过直线外一点有且只有一条直线和这直线平行)．

因为AB∥CD(已知)，AB∥EF(已作)，

∴CD∥EF(平行公理的推论)．

∴∠ABE＝∠1(两直线平行，内错角相等)．

∠CDE＝∠2(两直线平行，内错角相等)．

∴∠BED＝∠1＋∠2＝∠ABE＋∠CDE＝40°＋60°＝100°.

例3　如图，在△ABC中，CD⊥AB于D，FG⊥AB于G，∠1＝∠2.

试问ED∥BC吗？说说你的理由．

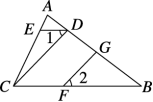
思路分析：已知中涉及的∠1与哪个角相等才能得到ED∥BC.已知∠1＝∠2，思考能否由已知条件先证出∠DCB＝∠2，再进一步得到∠1＝∠DCB，进而证出ED∥BC.

解：ED∥BC.

理由：∵CD⊥AB，FG⊥AB，

∴∠CDB＝∠FGB＝90°，

∴DC∥GF，

∴∠DCB＝∠2，又∠1＝∠2，

∴∠1＝∠DCB，

∴ED∥BC.

五、反馈训练

完成《作业与单元评估》随堂演练．

六、课堂小测

1．如图，直线a∥b，点B在直线b上，且AB⊥BC，∠1＝55°，则∠2的度数为(　A　)

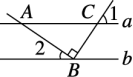
A．35°   B．45°

C．55°   D．125°

2．如图．

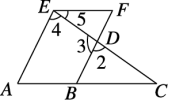
(1)若EF∥AC，则∠A＋__∠FEA__＝180°，∠F＋__∠ABF__＝180°，∠C＝__∠5__；

(2)若∠2＝__∠4__，则AE∥BF；

(3)若∠A＋__∠ABF__＝180°，则AE∥BF.

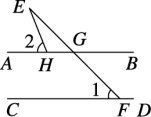
3．如图，直线AB∥CD，直线EF交AB于G，交CD于F，直线EH交AB于H.若∠1＝45°，∠2＝60°，则∠E的度数为__15°__.

4．如图所示，已知DE∥BC，DF，BE分别平分∠ADE，∠ABC.

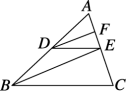
求证：∠FDE＝∠DEB.

证明：∵DE∥BC(已知)，

∴∠ADE＝∠ABC(两直线平行，同位角相等)．

∵DF，BE分别平分∠ADE，∠ABC(已知)，

∴∠ADF＝∠ADE＝∠ABC＝∠ABE(角平分线定义)．

∴DF∥BE(同位角相等，两直线平行)．

∴∠FDE＝∠DEB(两直线平等，内错角相等)．

七、课堂小结

1．完成一个命题的证明，有下列主要环节：

(1)根据命题，找出命题的条件和结论；

(2)根据命题画出图形，写出已知、求证；

(3)从已知条件出发，根据基本事实、定义、等式性质等，演绎推理出结论．

2．学习了平行线的性质．

八、布置作业

完成《作业与单元评估》课后作业的相关练习．