人教版九年级上册22.3 实际问题与二次函数学案

这是一份人教版九年级上册22.3 实际问题与二次函数学案，共26页。
中考数学高频考点突破：实际问题与二次函数——销售问题
1．我校九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相关信息如表：
时间x（天）
1≤x＜50
50≤x≤90
售价（元/件）
x+40
90
每天销量（件）
200﹣2x
已知该商品的进价为每件30元，设销售该商品的每天利润为y元．
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在第50天至90天的销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果．
2．恩施州绿色、富硒产品和特色农产品在国际市场上颇具竞争力，其中香菇远销日本和韩国等地．上市时，外商李经理按市场价格10元/千克在该州收购了2000千克香菇存放入冷库中．据预测，香菇的市场价格每天每千克将上涨0.5元，但冷库存放这批香菇时每天需要支出各种费用合计340元，而且香菇在冷库中最多保存110天，同时，平均每天有6千克的香菇损坏不能出售．
（1）若存放x天后，将这批香菇一次性出售，设这批香菇的销售总金额为y元，试写出y与x之间的函数关系式．
（2）李经理想获得利润22500元，需将这批香菇存放多少天后出售？（利润＝销售总金额﹣收购成本﹣各种费用）
（3）李经理将这批香菇存放多少天后出售可获得最大利润？最大利润是多少？
3．某竹制品加工厂根据市场调研结果，对该厂生产的一种新型竹制品玩具未来两年的销售进行预测，并建立如下模型：设第t个月，竹制品销售量为P（单位：箱），P与t之间存在如图所示函数关系，其图象是线段AB（不含点A）和线段BC的组合．设第t个月
销售每箱的毛利润为Q（百元），且Q与t满足如下关系Q＝2t+8（0≤t≤24）
（1）求P与t的函数关系式（6≤t≤24）．
（2）该厂在第几个月能够获得最大毛利润？最大毛利润是多少？


（3）经调查发现，当月毛利润不低于40000且不高于43200元时，该月产品原材料供给和市场售最和谐，此时称这个月为“和谐月”，那么，在未来两年中第几个月为和谐月？

4．我市某乡镇在“精准扶贫”活动中销售一农产品，经分析发现月销售量y（万件）与月份x（月）的关系为：y＝，每件产品的利润z（元）与月份x（月）的关系如下表：
x
1
2
3
4
5
6
7
8
9
10
11
12
z
19
18
17
16
15
14
13
12
11
10
10
10
（1）请你根据表格求出每件产品利润z（元）与月份x（月）的关系式；
（2）若月利润w（万元）＝当月销售量y（万件）×当月每件产品的利润z（元），求月利润w（万元）与月份x（月）的关系式；
（3）当x为何值时，月利润w有最大值，最大值为多少？
5．大学生小韩在暑假创业，销售一种进价为20元/件的玩具熊，销售过程中发现，每周销售量（件）与销售单价x（元）之间的关系可近似的看作一次函数：y＝﹣2x+100
（1）如果小韩想要每周获得400元的利润，那么销售单价应定为多少元？
（2）设小韩每周获得利润为w（元），当销售单价定为多少元时，每周可获得利润最大，最大利润是多少？
（3）若该玩具熊的销售单价不得高于34元，如果小韩想要每周获得的利润不低于400元，那么他的销售单价应定为多少？





6．某公司生产的某种时令商品每件成本为20元，经过市场调研发现：
①这种商品在未来40天内的日销售量m（件）与时间t（天）的关系如下表：
时间t（天）
1
3
6
10
36
…
日销售量m（件）
94
90
84
76
24
…
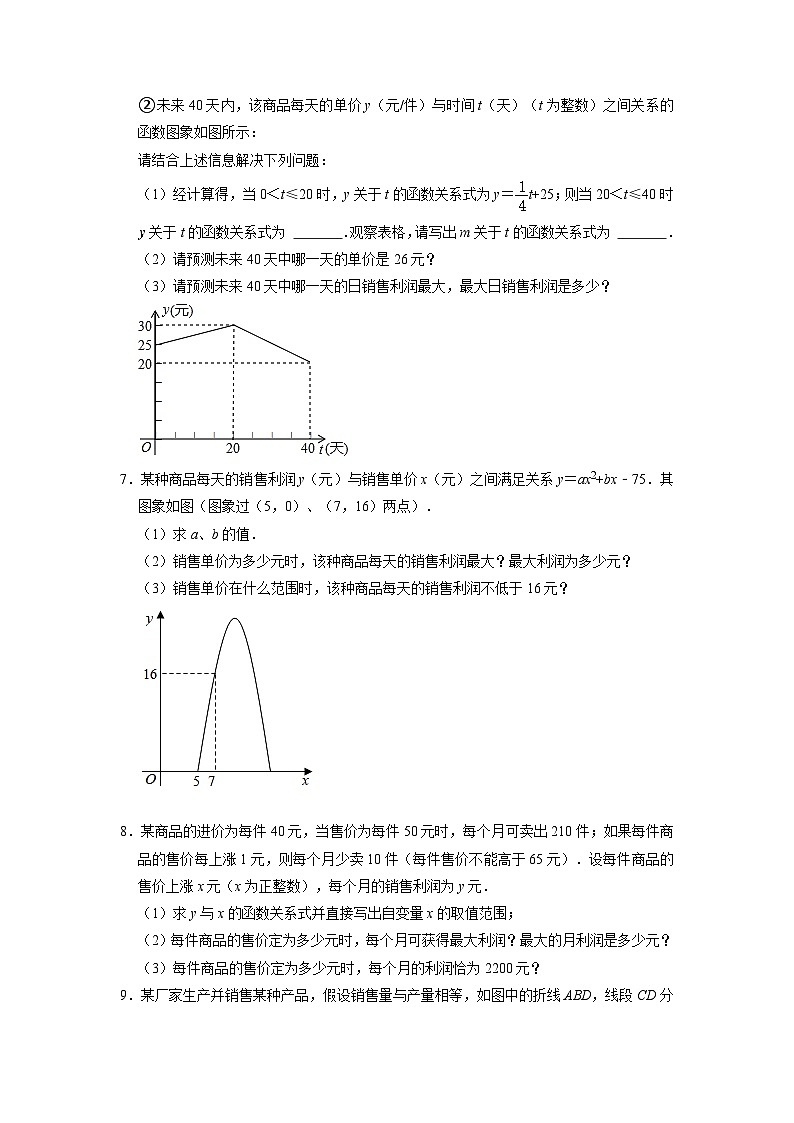
②未来40天内，该商品每天的单价y（元/件）与时间t（天）（t为整数）之间关系的函数图象如图所示：
请结合上述信息解决下列问题：
（1）经计算得，当0＜t≤20时，y关于t的函数关系式为y＝t+25；则当20＜t≤40时，y关于t的函数关系式为 　 　．观察表格，请写出m关于t的函数关系式为 　 　．
（2）请预测未来40天中哪一天的单价是26元？
（3）请预测未来40天中哪一天的日销售利润最大，最大日销售利润是多少？

7．某种商品每天的销售利润y（元）与销售单价x（元）之间满足关系y＝ax2+bx﹣75．其图象如图（图象过（5，0）、（7，16）两点）．
（1）求a、b的值．
（2）销售单价为多少元时，该种商品每天的销售利润最大？最大利润为多少元？
（3）销售单价在什么范围时，该种商品每天的销售利润不低于16元？


8．某商品的进价为每件40元，当售价为每件50元时，每个月可卖出210件；如果每件商品的售价每上涨1元，则每个月少卖10件（每件售价不能高于65元）．设每件商品的售价上涨x元（x为正整数），每个月的销售利润为y元．
（1）求y与x的函数关系式并直接写出自变量x的取值范围；
（2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？
（3）每件商品的售价定为多少元时，每个月的利润恰为2200元？
9．某厂家生产并销售某种产品，假设销售量与产量相等，如图中的折线ABD，线段CD分别表示该产品每千克生产成本y1（单位：元），销售价y2（单位：元）与产量x（单位：kg）之间的函数关系．
（1）请解释图中点D的实际意义．
（2）求线段CD所表示的y2与x之间的函数表达式．
（3）当该产品产量为多少时，获得的利润最大？最大利润是多少？

10．某玩具批发商销售每件进价为40元的玩具，市场调查发现，若以每件50元的价格销售，平均每天销售90件，单价每提高1元，平均每天就少销售3件．
（1）平均每天的销售量y（件）与销售价x（元/件）之间的函数关系式为　 　；
（2）求该批发商平均每天的销售利润W（元）与销售价x（元/件）之间的函数关系式；
（3）物价部门规定每件售价不得高于55元，当每件玩具的销售价为多少元时，可以获得最大利润？最大利润是多少元？
11．某商场经营某种品牌的玩具，购进时的单价是30元，根据市场调查：在一段时间内，销售单价是40元时，销售量是600件，而销售单价每涨1元，就会少售出10件玩具．
（1）如果设涨价为x元，销量为　 　．（请用含x的代数式表示）
（2）该玩具销售单价定为多少元时，商场能获得12000元的销售利润？
（3）若玩具厂规定该品牌玩具销售单价不低于46元，且商场要完成不少于500件的销售任务，求商场销售该品牌玩具获得的最大利润是多少．
12．某商场购进一批新型的电脑用于出售给与之合作的企业，每台电脑的成本为3600元，销售单价定为4500元，在该种电脑的试销期间，为了促销，鼓励企业积极购买该新型电脑，商场经理决定一次购买这种电脑不超过10台时，每台按4500元销售；若一次购买该种电脑超过10台时，每多购买一台，所购买的电脑的销售单价均降低50元，但销售单价均不低于3900元．
（1）企业一次购买这种电脑多少台时，销售单价恰好为3900元？
（2）设某企业一次购买这种电脑x台，商场所获得的利润为y元，求y（元）与x（台）之间的函数关系式，并写出自变量x的取值范围．若A企业欲购进一批该新型电脑（不超过25台），则A企业一次性购进多少台电脑时，商场获得的利润最大？
（3）该商场的销售人员发现：当企业一次购买电脑的台数超过某一数量时，会出现随着一次购买的数量的增多，商场所获得的利润反而减少这一情况，为使企业一次购买的数量越多，商场所获得的利润越大，商场应将最低销售单价调整为多少元？（其它销售条件不变）
13．由于雾霾天气对人们健康的影响，市场上的空气净化器成了热销产品．某公司经销一种空气净化器，每台净化器的成本价为200元．经过一段时间的销售发现，每月的销售量y（台）与销售单价x（元）的关系为y＝﹣2x+1000．
（1）该公司每月的利润为w元，写出利润w与销售单价x的函数关系式；
（2）若要使每月的利润为40000元，销售单价应定为多少元？
（3）公司要求销售单价不低于250元，也不高于400元，求该公司每月的最高利润和最低利润分别为多少？
14．某商场老板对一种新上市商品的销售情况进行记录，已知这种商品进价为每件40元，经过记录分析发现，当销售单价在40元至90元之间（含40元和90元）时，每月的销售量y（件）与销售单价x（元）之间的关系可近似地看作一次函数，其图象如图所示．
（1）求y与x的函数关系式．
（2）设商场老板每月获得的利润为P（元），求P与x之间的函数关系式；
（3）如果想要每月获得2400元的利润，那么销售单价应定为多少元？

15．某公司销售一种成本单价为50元/件的产品，规定销售单价不低于成本单价，又不高于80元/件，经调查，发现每天销售量y（件）与销售单价x（元/件）可近似于一次函数y＝kx+b的关系如图．
（1）根据图象，求一次函数y＝kx+b的解析式，并写出自变量x的取值范围．
（2）该公司要想每天获得600元的利润，且进货成本不超过1000元，那么该公司应把销售单价定为多少？．
（3）该公司要想每天获得最大的利润，应把销售单价定为多少？最大利润值为多少？

16．铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀．小张购进一批食材制作特色美食，每盒售价为50元，由于食材需要冷藏保存，导致成本逐日增加，第x天（1≤x≤15且x为整数）时每盒成本为p元，已知p与x之间满足一次函数关系；第3天时，每盒成本为21元；第7天时，每盒成本为25元，每天的销售量为y盒，y与x之间的关系如下表所示：
第x天
1≤x≤6
6＜x≤15
每天的销售量y/盒
10
x+6
（1）求p与x的函数关系式；
（2）若每天的销售利润为w元，求w与x的函数关系式，并求出第几天时当天的销售利润最大，最大销售利润是多少元？
（3）在“荷花美食”厨艺秀期间，共有多少天小张每天的销售利润不低于325元？请直接写出结果．
17．大润发超市在销售某种进货价为20元/件的商品时，以30元/件售出，每天能售出100件．调查表明：这种商品的售价每上涨1元/件，其销售量就将减少2件．
（1）为了实现每天1600元的销售利润，超市应将这种商品的售价定为多少？
（2）设每件商品的售价为x元，超市所获利润为y元．
①求y与x之间的函数关系式；
②物价局规定该商品的售价不能超过40元/件，超市为了获得最大的利润，应将该商品售价定为多少？最大利润是多少？
18．某公司购进某种水果的成本为20元/千克，经过市场调研发现，这种水果在未来48天的销售价格p（元/千克）与时间t（天）之间的函数关系式为
p＝，且其日销售量y（千克）与时间t（天）的关系如下表：
时间t/天
1
3
6
10
20
40
…
日销售量y/千克
118
114
108
100
80
40
…
（1）已知y与t之间的变化规律符合一次函数关系，试求在第30天的日销售量是多少？
（2）问哪一天的销售利润最大？最大日销售利润为多少？
（3）在实际销售的前24天中，公司决定每销售1千克水果就捐赠n元利润（n＜9）给“精准扶贫”对象．现发现：在前24天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，求n的取值范围．
19．市政府大力扶持大学生创业，小明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价（x）元之间的关系可近似地看作一次函数y＝﹣10x+500．
（1）设小明每月获得的利润为W（元），当销售单价定为多少元时，每月可获得最大利润？
（2）如果小明想要每月获得2000元的利润，那么销售单价应定为多少元？
（3）根据物价部门规定，这种护眼台灯的销售单价不得高于35元，如果小明想要每月获得的利润不低于2000元，那么他每月的成本最多需要多少元？（成本＝进价×销售量）








20．九年级（3）班数学兴趣小组经过市场调查整理出某种商品在第x天（1≤x≤90，且x为整数）的售价与销售量的相关信息如下．已知商品的进价为30元/件，设该商品的售价为y（单位：元/件），每天的销售量为p（单位：件），每天的销售利润为w（单位：元）．
时间x（天）
1
30
60
90
每天销售量p（件）
198
140
80
20
（1）求出w与x的函数关系式；
（2）问销售该商品第几天时，当天的销售利润最大？并求出最大利润；
（3）该商品在销售过程中，共有多少天每天的销售利润不低于5600元？请直接写出结果．
















参考答案与试题解析
1．我校九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相关信息如表：
时间x（天）
1≤x＜50
50≤x≤90
售价（元/件）
x+40
90
每天销量（件）
200﹣2x
已知该商品的进价为每件30元，设销售该商品的每天利润为y元．
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在第50天至90天的销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果．
【解答】解：（1）当1≤x＜50时，y＝（200﹣2x）（x+40﹣30）＝﹣2x2+180x+2000，
当50≤x≤90时，y＝（200﹣2x）（90﹣30）＝﹣120x+12000，
综上所述：y＝；
（2）当1≤x＜50时，
二次函数y＝﹣2x2+180x+2000的图象开口向下，对称轴为x＝45，
当x＝45时，y最大＝﹣2×452+180×45+2000＝6050，
当50≤x≤90时，
y＝﹣120x+12000中y随x的增大而减小，
∴当x＝50时，y最大＝6000，
综上所述，该商品第45天时，当天销售利润最大，最大利润是6050元；
（3）该商品第50天至90天的在销售过程中，共11天每天销售利润不低于4800元，
理由：当50≤x≤90时，
﹣120x+12000≥4800，
解得x≤60，
∴利润不低于4800元的天数是50≤x≤60，共11天，
即该商品第50天至90天的在销售过程中，共11天每天销售利润不低于4800元．
2．恩施州绿色、富硒产品和特色农产品在国际市场上颇具竞争力，其中香菇远销日本和韩国等地．上市时，外商李经理按市场价格10元/千克在该州收购了2000千克香菇存放入冷库中．据预测，香菇的市场价格每天每千克将上涨0.5元，但冷库存放这批香菇时每天需要支出各种费用合计340元，而且香菇在冷库中最多保存110天，同时，平均每天有6千克的香菇损坏不能出售．
（1）若存放x天后，将这批香菇一次性出售，设这批香菇的销售总金额为y元，试写出y与x之间的函数关系式．
（2）李经理想获得利润22500元，需将这批香菇存放多少天后出售？（利润＝销售总金额﹣收购成本﹣各种费用）
（3）李经理将这批香菇存放多少天后出售可获得最大利润？最大利润是多少？
【解答】解：（1）由题意y与x之间的函数关系式为y＝（10+0.5x）（2000﹣6x），
＝﹣3x2+940x+20000（1≤x≤110，且x为整数）；
（2）由题意得：
﹣3x2+940x+20000﹣10×2000﹣340x＝22500
解方程得：x1＝50，x2＝150（不合题意，舍去）
李经理想获得利润22500元需将这批香菇存放50天后出售；
（3）设利润为w，由题意得
w＝﹣3x2+940x+20000﹣10×2000﹣340x＝﹣3（x﹣100）2+30000
∵a＝﹣3＜0，
∴抛物线开口方向向下，
∴x＝100时，w最大＝30000
100天＜110天
∴存放100天后出售这批香菇可获得最大利润30000元．
3．某竹制品加工厂根据市场调研结果，对该厂生产的一种新型竹制品玩具未来两年的销售进行预测，并建立如下模型：设第t个月，竹制品销售量为P（单位：箱），P与t之间存在如图所示函数关系，其图象是线段AB（不含点A）和线段BC的组合．设第t个月
销售每箱的毛利润为Q（百元），且Q与t满足如下关系Q＝2t+8（0≤t≤24）
（1）求P与t的函数关系式（6≤t≤24）．
（2）该厂在第几个月能够获得最大毛利润？最大毛利润是多少？
（3）经调查发现，当月毛利润不低于40000且不高于43200元时，该月产品原材料供给和市场售最和谐，此时称这个月为“和谐月”，那么，在未来两年中第几个月为和谐月？

【解答】解：（1）当6≤t≤24时，设P与t的函数关系式为P＝kt+b
∵该图象过点B（6，20）和C（24，2）
∴
∴
∴P与t的函数关系式为P＝﹣t+26（6≤t≤24）．
（2）设直线AB的函数解析式为P＝mt+n，将A（0，14），B （6，20）代入得：

∴
∴直线AB的函数解析式为P＝t+14
∴当0＜t＜6时，
利润L＝QP＝（2t+8）（t+14）＝2t2+36t+112＝2（t+9）2﹣50
当t＝5时，利润L取最大值为2（5+9）2﹣50＝342（百元）＝34200（元）；
当6≤t≤24时，
利润L＝QP＝（2t+8）（﹣t+26）＝﹣2t2+44t+208＝﹣2（t﹣11）2+450
450百元＝45000元
∴当t＝11时，利润L有最大值，最大值为45000元．
综上，该厂在第11个月能够获得最大毛利润，最大毛利润是45000元．
（3）∵40000元＝400元，43200元＝432百元
∴或
第一个不等式无解，第二个不等式的解为6≤t≤8或14≤t≤16
∴未来两年中的和谐月有：6，7，8，14，15，16这六个月．
4．我市某乡镇在“精准扶贫”活动中销售一农产品，经分析发现月销售量y（万件）与月份x（月）的关系为：y＝，每件产品的利润z（元）与月份x（月）的关系如下表：
x
1
2
3
4
5
6
7
8
9
10
11
12
z
19
18
17
16
15
14
13
12
11
10
10
10
（1）请你根据表格求出每件产品利润z（元）与月份x（月）的关系式；
（2）若月利润w（万元）＝当月销售量y（万件）×当月每件产品的利润z（元），求月利润w（万元）与月份x（月）的关系式；
（3）当x为何值时，月利润w有最大值，最大值为多少？
【解答】解；（1）当1≤x≤9时，设每件产品利润z（元）与月份x（月）的关系式为z＝kx+b，
，得，
即当1≤x≤9时，每件产品利润z（元）与月份x（月）的关系式为z＝﹣x+20，
当10≤x≤12时，z＝10，
由上可得，z＝；
（2）当1≤x≤8时，
w＝（x+4）（﹣x+20）＝﹣x2+16x+80，
当x＝9时，
w＝（﹣9+20）×（﹣9+20）＝121，
当10≤x≤12时，
w＝（﹣x+20）×10＝﹣10x+200，
由上可得，w＝；
（3）当1≤x≤8时，w＝﹣x2+16x+80＝﹣（x﹣8）2+144，
∴当x＝8时，w取得最大值，此时w＝144；
当x＝9时，w＝121，
当10≤x≤12时，w＝﹣10x+200，
则当x＝10时，w取得最大值，此时w＝100，
由上可得，当x为8时，月利润w有最大值，最大值144万元．
5．大学生小韩在暑假创业，销售一种进价为20元/件的玩具熊，销售过程中发现，每周销售量（件）与销售单价x（元）之间的关系可近似的看作一次函数：y＝﹣2x+100
（1）如果小韩想要每周获得400元的利润，那么销售单价应定为多少元？
（2）设小韩每周获得利润为w（元），当销售单价定为多少元时，每周可获得利润最大，最大利润是多少？
（3）若该玩具熊的销售单价不得高于34元，如果小韩想要每周获得的利润不低于400元，那么他的销售单价应定为多少？
【解答】解：（1）根据题意可得：（x﹣20）（﹣2x+100）＝400，
解得：x＝30或x＝40，
答：销售单价应定为30元或40元；

（2）w＝（x﹣20）（﹣2x+100）＝﹣2x2+140x﹣2000＝﹣2（x﹣35）2+450，
∴当x＝35时，w取得最大值，最大值为450元，
答：当售价为35元/台时，最大利润为450元；

（3）根据题意有：（x﹣20）（﹣2x+100）≥400，
解得：30≤x≤40，
又x≤34，
∴30≤x≤34，
答：他的销售单价应定为30元至34元之间．
6．某公司生产的某种时令商品每件成本为20元，经过市场调研发现：
①这种商品在未来40天内的日销售量m（件）与时间t（天）的关系如下表：
时间t（天）
1
3
6
10
36
…
日销售量m（件）
94
90
84
76
24
…
②未来40天内，该商品每天的单价y（元/件）与时间t（天）（t为整数）之间关系的函数图象如图所示：
请结合上述信息解决下列问题：
（1）经计算得，当0＜t≤20时，y关于t的函数关系式为y＝t+25；则当20＜t≤40时，y关于t的函数关系式为 　y＝﹣t+40　．观察表格，请写出m关于t的函数关系式为 　m＝﹣2t+96　．
（2）请预测未来40天中哪一天的单价是26元？
（3）请预测未来40天中哪一天的日销售利润最大，最大日销售利润是多少？

【解答】解：（1）当20＜t≤40时，y关于t的函数关系式为y＝at+b，
则，
解得：，
∴y关于t的函数关系式为 y＝﹣t+40；
通过表中数据知，m与t成一次函数关系，设m＝kt+c，
将t＝1，m＝94，t＝3，m＝90代入，得：
，
解得：，
∴m与t的函数关系为m＝﹣2t+96．
故答案为：y＝﹣t+40；m＝﹣2t+96；
（2）①当0＜t≤20时，
令t+25＝26，
解得：t＝4，
②当20＜t≤40时，
令﹣t+40＝26，
解得：t＝28，
∴未来40天中第4天和第28天的单价是26元；
（3）前20天的销售利润为P1元，后20天的销售利润为P2元，
则P1＝（﹣2t+96）（t+25﹣20）
＝﹣（t﹣14）2+578，
∵﹣＜0，
∴当t＝14时，P1有最大值，为578元；
P2＝（﹣2t+96）（﹣t+40﹣20）
＝t2﹣88t+1920
＝（t﹣44）2﹣16，
∵1＞0，
∴当21≤t≤40时，P2随t的增大而减小，
∴当t＝21时，P2最大，为513元，
∴第14天利润最大，最大利润为578元．
7．某种商品每天的销售利润y（元）与销售单价x（元）之间满足关系y＝ax2+bx﹣75．其图象如图（图象过（5，0）、（7，16）两点）．
（1）求a、b的值．
（2）销售单价为多少元时，该种商品每天的销售利润最大？最大利润为多少元？
（3）销售单价在什么范围时，该种商品每天的销售利润不低于16元？

【解答】解：（1）由图象可得出：图象过（5，0），（7，16）点，
故，
解得：，
∴a＝﹣1，b＝20；
（2）由（1）知，y＝﹣x2+20x﹣75＝﹣（x﹣10）2+25，
∵﹣1＜0，
∴当x＝10时，y有最大值，最大值为25，
答：当销售单价为10元时，该种商品每天的销售利润最大，最大利润为25元；
（3）∵函数y＝﹣x2+20x﹣75图象的对称轴为直线x＝10，
可知点（7，16）关于对称轴的对称点是（13，16），
又∵函数y＝﹣x2+20x﹣75图象开口向下，
∴当7≤x≤13时，y≥16．
答：销售单价不少于7元且不超过13元时，该种商品每天的销售利润不低于16元．
8．某商品的进价为每件40元，当售价为每件50元时，每个月可卖出210件；如果每件商品的售价每上涨1元，则每个月少卖10件（每件售价不能高于65元）．设每件商品的售价上涨x元（x为正整数），每个月的销售利润为y元．
（1）求y与x的函数关系式并直接写出自变量x的取值范围；
（2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？
（3）每件商品的售价定为多少元时，每个月的利润恰为2200元？
【解答】解：（1）y＝（210﹣10x）（50+x﹣40）＝﹣10x2+110x+2100（0＜x≤15且x为整数）；

（2）由（1）中的y与x的解析式配方得：y＝﹣10（x﹣5.5）2+2402.5．
∵a＝﹣10＜0，∴当x＝5.5时，y有最大值2402.5．
∵0＜x≤15，且x为整数，
当x＝5时，50+x＝55，y＝2400（元），
当x＝6时，50+x＝56，y＝2400（元），
∴当售价定为每件55或56元，每个月的利润最大，最大的月利润是2400元．

（3）当y＝2200时，﹣10x2+110x+2100＝2200，
解得：x1＝1，x2＝10．
∴当x＝1时，50+x＝51，
当x＝10时，50+x＝60，
∴当售价定为每件51元或60元，每个月的利润为2200元．
9．某厂家生产并销售某种产品，假设销售量与产量相等，如图中的折线ABD，线段CD分别表示该产品每千克生产成本y1（单位：元），销售价y2（单位：元）与产量x（单位：kg）之间的函数关系．
（1）请解释图中点D的实际意义．
（2）求线段CD所表示的y2与x之间的函数表达式．
（3）当该产品产量为多少时，获得的利润最大？最大利润是多少？

【解答】解：（1）点D的实际意义：当产量为140kg时，该产品每千克生产成本与销售价相等，都为40元．

（2）设线段CD所表示的y2与x之间的函数表达式为y2＝k1x+b1，
∵点（0，124），（140，40）在函数y2＝k1x+b1的图象上
∴，解得：，
∴y2与x之间的函数表达式为y2＝﹣x+124（0≤x≤140）；

（3）设线段AB所表示的y1与x之间的函数表达式为y1＝k2x+b2，
∵点（0，60），（100，40）在函数y1＝k2x+b2的图象上
∴，解得：，
∴y1与x之间的函数表达式为y1＝﹣x+60（0≤x≤100）
设产量为x千克时，获得的利润为W元
①当0≤x≤100时，W＝[（﹣x+124）﹣（﹣x+60）]x＝﹣（x﹣80）2+2560，
∴当x＝80时，W的值最大，最大值为2560元．
②当100≤x≤140时，W＝[（﹣x+124）﹣40]x＝﹣（x﹣70）2+2940
由﹣＜0知，当x≥70时，W随x的增大而减小
∴当x＝100时，W的值最大，最大值为2400元．
∵2560＞2400，
∴当该产品的质量为80kg时，获得的利润最大，最大利润为2560元．
10．某玩具批发商销售每件进价为40元的玩具，市场调查发现，若以每件50元的价格销售，平均每天销售90件，单价每提高1元，平均每天就少销售3件．
（1）平均每天的销售量y（件）与销售价x（元/件）之间的函数关系式为　y＝﹣3x+240　；
（2）求该批发商平均每天的销售利润W（元）与销售价x（元/件）之间的函数关系式；
（3）物价部门规定每件售价不得高于55元，当每件玩具的销售价为多少元时，可以获得最大利润？最大利润是多少元？
【解答】解：（1）由题意得：y＝90﹣3（x﹣50）＝﹣3x+240；

（2）W＝（x﹣40）（﹣3x+240）＝﹣3x2+360x﹣9600；

（3）y＝﹣3x2+360x﹣9600＝﹣3（x﹣60）2+1200，
故当x＝60时，y取最大值1200，
∵x＝60是二次函数的对称轴，且开口向下，
∴当x＜60时，y随x的增大而增大，
∵规定每件售价不得高于55元，
∴当x＝55时，W取得最大值为1125元，
即每件玩具的销售价为55元时，可获得1125元的最大利润．
11．某商场经营某种品牌的玩具，购进时的单价是30元，根据市场调查：在一段时间内，销售单价是40元时，销售量是600件，而销售单价每涨1元，就会少售出10件玩具．
（1）如果设涨价为x元，销量为　（600﹣10x）　．（请用含x的代数式表示）
（2）该玩具销售单价定为多少元时，商场能获得12000元的销售利润？
（3）若玩具厂规定该品牌玩具销售单价不低于46元，且商场要完成不少于500件的销售任务，求商场销售该品牌玩具获得的最大利润是多少．
【解答】解：（1）由题意得：如果设涨价为x元，销量为：600﹣10x，
故答案为：（600﹣10x）；

（2）设：该玩具销售单价定为y元时，商场能获得1200元的销售利润，
由题意得：（y﹣30）[600﹣（y﹣40）×10]＝12000，
即﹣10（y﹣100）（y﹣30）＝12000，
解得：y＝60或70，
答：销售单价定为60或70元时，商场能获得12000元的销售利润；

（3）设销售单价为m元时，获得的利润时w元，
由题意得：m≥46，600﹣（m﹣40）×10≥500，解得：46≤m≤50，
则w＝﹣10（m﹣100）（m﹣30），
∵﹣10＜0，故w有最大值，
当m＜（100+30）＝65时，w随m的增大而增大，
∴当m＝50时，w的最大值为：10000，
答：商场销售该品牌玩具获得的最大利润是10000元．
12．某商场购进一批新型的电脑用于出售给与之合作的企业，每台电脑的成本为3600元，销售单价定为4500元，在该种电脑的试销期间，为了促销，鼓励企业积极购买该新型电脑，商场经理决定一次购买这种电脑不超过10台时，每台按4500元销售；若一次购买该种电脑超过10台时，每多购买一台，所购买的电脑的销售单价均降低50元，但销售单价均不低于3900元．
（1）企业一次购买这种电脑多少台时，销售单价恰好为3900元？
（2）设某企业一次购买这种电脑x台，商场所获得的利润为y元，求y（元）与x（台）之间的函数关系式，并写出自变量x的取值范围．若A企业欲购进一批该新型电脑（不超过25台），则A企业一次性购进多少台电脑时，商场获得的利润最大？
（3）该商场的销售人员发现：当企业一次购买电脑的台数超过某一数量时，会出现随着一次购买的数量的增多，商场所获得的利润反而减少这一情况，为使企业一次购买的数量越多，商场所获得的利润越大，商场应将最低销售单价调整为多少元？（其它销售条件不变）
【解答】解：（1）设购买x台时，单价恰为3900元，
则4500﹣50（x﹣10）＝3900，
解得：x＝22
故购买22台时，销售单价恰为3900元；
（2）商场所获得的利润为y元与x（台）之间的函数关系式有如下三种情况：
①当0≤x≤10时，y＝（4500﹣3600）x＝900x，
②当10＜x≤22时，y＝x[4500﹣50（x﹣10）﹣3600]＝﹣50x2+1400x，
③当x＞22时，y＝（3900﹣3600）x＝300x；
商场若要获得最大利润，
①当0≤x≤10时，∵y＝900x，y随x增大而增大，
∴当x＝10时，y最大且最大值为9000；
②当10＜x≤22时，∵y＝﹣50x2+1400x＝﹣50（x﹣14）2+9800，
∴当x＝14时，y最大且最大值为9800；
③当 22＜x≤25时，∵y＝300x，y随x增大而增大，
∴当x＝25时，y最大且最大值为7500；
∵7500＜9000＜9800，
∴一次性购买14台电脑时，利润最大且为9800元
（3）①当0≤x≤10时 y＝900x
∵900＞0，∴y随x增大而增大
②当10＜x≤22时，y＝﹣50x2+1400x＝﹣50（x﹣14）2+9800，
∵﹣50＜0，
∴当10＜x≤14时，y随x增大而增大
当14＜x≤22时，y随x增大而减小
∴最低单价应调为4500﹣50（14﹣10）＝4300元
综上，商场应将最低销售单价调为4300元．
13．由于雾霾天气对人们健康的影响，市场上的空气净化器成了热销产品．某公司经销一种空气净化器，每台净化器的成本价为200元．经过一段时间的销售发现，每月的销售量y（台）与销售单价x（元）的关系为y＝﹣2x+1000．
（1）该公司每月的利润为w元，写出利润w与销售单价x的函数关系式；
（2）若要使每月的利润为40000元，销售单价应定为多少元？
（3）公司要求销售单价不低于250元，也不高于400元，求该公司每月的最高利润和最低利润分别为多少？
【解答】解：（1）由题意得：w＝（x﹣200）y＝（x﹣200）（﹣2x+1000）＝﹣2x2+1400x﹣200000；

（2）令w＝﹣2x2+1400x﹣200000＝40000，
解得：x＝300或x＝400，
故要使每月的利润为40000元，销售单价应定为300或400元；

（3）y＝﹣2x2+1400x﹣200000＝﹣2（x﹣350）2+45000，
当x＝250时y＝﹣2×2502+1400×250﹣200000＝25000；
故最高利润为45000元，最低利润为25000元．
14．某商场老板对一种新上市商品的销售情况进行记录，已知这种商品进价为每件40元，经过记录分析发现，当销售单价在40元至90元之间（含40元和90元）时，每月的销售量y（件）与销售单价x（元）之间的关系可近似地看作一次函数，其图象如图所示．
（1）求y与x的函数关系式．
（2）设商场老板每月获得的利润为P（元），求P与x之间的函数关系式；
（3）如果想要每月获得2400元的利润，那么销售单价应定为多少元？

【解答】解：（1）设y与x的函数关系式为：y＝kx+b（k≠0），
由题意得，
解得．
故y＝﹣4x+360（40≤x≤90）；

（2）由题意得，P与x的函数关系式为：
P＝（x﹣40）（﹣4x+360）＝﹣4x2+520x﹣14400，

（3）当P＝2400时，
﹣4x2+520x﹣14400＝2400，
解得：x1＝60，x2＝70，
故销售单价应定为60元或70元．
15．某公司销售一种成本单价为50元/件的产品，规定销售单价不低于成本单价，又不高于80元/件，经调查，发现每天销售量y（件）与销售单价x（元/件）可近似于一次函数y＝kx+b的关系如图．
（1）根据图象，求一次函数y＝kx+b的解析式，并写出自变量x的取值范围．
（2）该公司要想每天获得600元的利润，且进货成本不超过1000元，那么该公司应把销售单价定为多少？．
（3）该公司要想每天获得最大的利润，应把销售单价定为多少？最大利润值为多少？

【解答】解：（1）由函数的图象得：，
解得：，
∴y＝﹣x+100（50≤x≤80）；
（2）由题意得50（﹣x+100）≤1000，
解得：x≥80，
由（1）得：600＝（x﹣50）y＝（x﹣50）（﹣x+100），
即x2﹣150x+5600＝0，
解得：x1＝70（不合题意，舍去），x2＝80，
所以该公司应把销售单价定为80元/件；
（3）设每天获得的利润为W，
由（1）得：w＝（x﹣50）y＝（x﹣50）（﹣x+100）＝﹣x2+150x﹣5000，＝﹣（x﹣75）2+625，
∵﹣1＜0，
∴当x＝75时，w最大＝625，
即该公司要想每天获得最大的利润，应把销售单价定为75元/件，最大利润值为625元．
16．铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀．小张购进一批食材制作特色美食，每盒售价为50元，由于食材需要冷藏保存，导致成本逐日增加，第x天（1≤x≤15且x为整数）时每盒成本为p元，已知p与x之间满足一次函数关系；第3天时，每盒成本为21元；第7天时，每盒成本为25元，每天的销售量为y盒，y与x之间的关系如下表所示：
第x天
1≤x≤6
6＜x≤15
每天的销售量y/盒
10
x+6
（1）求p与x的函数关系式；
（2）若每天的销售利润为w元，求w与x的函数关系式，并求出第几天时当天的销售利润最大，最大销售利润是多少元？
（3）在“荷花美食”厨艺秀期间，共有多少天小张每天的销售利润不低于325元？请直接写出结果．
【解答】解：（1）设p＝kx+b（k≠0），
∵第3天时，每盒成本为21元；第7天时，每盒成本为25元，
∴，
解得，
所以，p＝x+18；

（2）1≤x≤6时，w＝10[50﹣（x+18）]＝﹣10x+320，
6＜x≤15时，w＝[50﹣（x+18）]（x+6）＝﹣x2+26x+192，
所以，w与x的函数关系式为w＝，
1≤x≤6时，∵﹣10＜0，
∴w随x的增大而减小，
∴当x＝1时，w最大为﹣10+320＝310，
6＜x≤15时，w＝﹣x2+26x+192＝﹣（x﹣13）2+361，
∴当x＝13时，w最大为361，
综上所述，第13天时当天的销售利润最大，最大销售利润是361元；

（3）w＝325时，﹣x2+26x+192＝325，
x2﹣26x+133＝0，
解得x1＝7，x2＝19，
所以，7≤x≤15时，即第7、8、9、10、11、12、13、14、15天共9天销售利润不低于325元．
17．大润发超市在销售某种进货价为20元/件的商品时，以30元/件售出，每天能售出100件．调查表明：这种商品的售价每上涨1元/件，其销售量就将减少2件．
（1）为了实现每天1600元的销售利润，超市应将这种商品的售价定为多少？
（2）设每件商品的售价为x元，超市所获利润为y元．
①求y与x之间的函数关系式；
②物价局规定该商品的售价不能超过40元/件，超市为了获得最大的利润，应将该商品售价定为多少？最大利润是多少？
【解答】解：（1）设商品的定价为x元，由题意，得
（x﹣20）[100﹣2（x﹣30）]＝1600，
解得：x＝40或x＝60；
答：售价应定为40元或60元．

（2）①y＝（x﹣20）[100﹣2（x﹣30）]（x≤40），
即y＝﹣2x2+200x﹣3200；
②∵a＝﹣2＜0，
∴当x＝＝50时，y取最大值；
又x≤40，则在x＝40时，y取最大值，即y最大值＝1600，
答：售价为40元/件时，此时利润最大，最大利润为1600元．
18．某公司购进某种水果的成本为20元/千克，经过市场调研发现，这种水果在未来48天的销售价格p（元/千克）与时间t（天）之间的函数关系式为
p＝，且其日销售量y（千克）与时间t（天）的关系如下表：
时间t/天
1
3
6
10
20
40
…
日销售量y/千克
118
114
108
100
80
40
…
（1）已知y与t之间的变化规律符合一次函数关系，试求在第30天的日销售量是多少？
（2）问哪一天的销售利润最大？最大日销售利润为多少？
（3）在实际销售的前24天中，公司决定每销售1千克水果就捐赠n元利润（n＜9）给“精准扶贫”对象．现发现：在前24天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，求n的取值范围．
【解答】解：（1）设y＝kt+b，把t＝1，y＝118；t＝3，y＝114代入得到：
，
解得：，
∴y＝﹣2t+120．
将t＝30代入上式，得：y＝﹣2×30+120＝20．
所以在第30天的日销售量是60kg．

（2）设第t天的销售利润为w元．
当1≤t≤24时，由题意w＝（﹣2t+120）（t+30﹣20）＝﹣（t﹣10）2+1250，
∴t＝10时 w最大值为1250元．
当25≤t≤48时，w＝（﹣2t+120）（﹣t+48﹣20）＝t2﹣116t+3360，
∵对称轴t＝58，a＝1＞0，
∴在对称轴左侧w随x增大而减小，
∴t＝25时，w最大值＝1085，
综上所述第10天利润最大，最大利润为1250元．

（3）设每天扣除捐赠后的日销售利润为m元．
由题意m＝（﹣2t+120）（t+30﹣20）﹣（﹣2t+120）n＝﹣t2+（10+2n）t+1200﹣120n，
∵在前24天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，
∴﹣＞23.5，
∴n＞6.75．
又∵n＜9，
∴n的取值范围为6.75＜n＜9．
19．市政府大力扶持大学生创业，小明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价（x）元之间的关系可近似地看作一次函数y＝﹣10x+500．
（1）设小明每月获得的利润为W（元），当销售单价定为多少元时，每月可获得最大利润？
（2）如果小明想要每月获得2000元的利润，那么销售单价应定为多少元？
（3）根据物价部门规定，这种护眼台灯的销售单价不得高于35元，如果小明想要每月获得的利润不低于2000元，那么他每月的成本最多需要多少元？（成本＝进价×销售量）
【解答】（1）解：W＝（﹣10x+500）（x﹣20）
＝﹣10x2+700x﹣10000
＝﹣10（x﹣35）2+2250
∴当x＝35时，每月可获得最大利润2250元

（2）﹣10（x﹣35）2+2250＝2000
得x1＝30，x2＝40
∴当销售价定为30或40元时，小明每月获得2000元利润．

（3）y＝﹣10x+500
∵﹣10＜0，∴y随x的增大而减小
∴当x取30时，成本最多
即成本＝20×（﹣10×30+500）
＝20×200
＝4000（元）
20．九年级（3）班数学兴趣小组经过市场调查整理出某种商品在第x天（1≤x≤90，且x为整数）的售价与销售量的相关信息如下．已知商品的进价为30元/件，设该商品的售价为y（单位：元/件），每天的销售量为p（单位：件），每天的销售利润为w（单位：元）．
时间x（天）
1
30
60
90
每天销售量p（件）
198
140
80
20
（1）求出w与x的函数关系式；
（2）问销售该商品第几天时，当天的销售利润最大？并求出最大利润；
（3）该商品在销售过程中，共有多少天每天的销售利润不低于5600元？请直接写出结果．

【解答】解：（1）当1≤x≤50时，设商品的售价y与时间x的函数关系式为y＝kx+b（k、b为常数且k≠0），
∵y＝kx+b经过点（0，40）、（50，90），
∴，解得：，
∴售价y与时间x的函数关系式为y＝x+40；
当50≤x≤90时，y＝90．
∴售价y与时间x的函数关系式为y＝．
由数据可知每天的销售量p与时间x成一次函数关系，
设每天的销售量p与时间x的函数关系式为p＝mx+n（m、n为常数，且m≠0），
∵p＝mx+n过点（60，80）、（30，140），
∴，解得：，
∴p＝﹣2x+200（1≤x≤90，且x为整数），
当1≤x≤50时，w＝（y﹣30）•p＝（x+40﹣30）（﹣2x+200）＝﹣2x2+180x+2000；
当50≤x≤90时，w＝（90﹣30）（﹣2x+200）＝﹣120x+12000．
综上所示，每天的销售利润w与时间x的函数关系式是w＝．
（2）当1≤x≤50时，w＝﹣2x2+180x+2000＝﹣2（x﹣45）2+6050，
∵a＝﹣2＜0且1≤x≤50，
∴当x＝45时，w取最大值，最大值为6050元．
当50≤x≤90时，w＝﹣120x+12000，
∵k＝﹣120＜0，w随x增大而减小，
∴当x＝50时，w取最大值，最大值为6000元．
∵6050＞6000，
∴当x＝45时，w最大，最大值为6050元．
即销售第45天时，当天获得的销售利润最大，最大利润是6050元．
（3）当1≤x≤50时，令w＝﹣2x2+180x+2000≥5600，即﹣2x2+180x﹣3600≥0，
解得：30≤x≤50，
50﹣30+1＝21（天）；
当50≤x≤90时，令w＝﹣120x+12000≥5600，即﹣120x+6400≥0，
解得：50≤x≤53，
∵x为整数，
∴50≤x≤53，
53﹣50+1＝4（天）．
综上可知：21+4﹣1＝24（天），
故该商品在销售过程中，共有24天每天的销售利润不低于5600元．