初中数学北师大版八年级上册3 勾股定理的应用精品巩固练习

这是一份初中数学北师大版八年级上册3 勾股定理的应用精品巩固练习，文件包含答案1docx、原卷1docx等2份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。

北师大版 数学 八上 第一章 2.3勾股定理的应用
一， 选择题（共30分）
1.勾股定理是人类最伟大的科学发现之一，在我国古算书 《周髀算经》 中早有记载。如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积，则一定能求出（　　）

A．直角三角形的面积
B．最大正方形的面积
C．较小两个正方形重叠部分的面积
D．最大正方形与直角三角形的面积和
【答案】C
【知识点】勾股定理的应用
【解析】【解答】解：根据勾股定理及正方形的面积计算方法可知：较小两个直角三角形的面积之和=较大正方形的面积，所以将三个正方形按图2方式放置的时候，较小两正方形重叠部分的面积=阴影部分的面积，所以知道了图2阴影部分的面积即可知道两小正方形重叠部分的面积。
故答案为：C
2.．代数式 x2+4+(12−x)2+9 的最小值为（　　）
A．12 B．13 C．14 D．11
【答案】B
【知识点】线段的性质：两点之间线段最短；勾股定理的应用
【解析】【解答】解：如图所示：

设P点坐标为P（x，0），
原式可化为 (x−0)2+[0−(−2)]2 + (x−12)2+(0−3)2 ，
即 (x−0)2+[0−(−2)]2 ＝AP， (x−12)2+(0−3)2 ＝BP，
AB＝ 122+52 ＝13．
代数式 x2+4+(12−x)2+9 的最小值为13．
故答案为：B．
3.甲乙两艘客轮同时离开港口，航行的速度都是40 m／min，甲客轮15min到达点A，乙客轮用20 min到达B点，若A，B两点的直线距离为1000 m.甲客轮沿北偏东30°的方向航行，则乙客轮的航行方向可能是(　　)
A．南偏东60° B．南偏西30° C．北偏西30° D．南偏西60°
【答案】A
【知识点】勾股定理的应用
【解析】【解答】设始发港口为C，则CA=15×40=600 , CB=20×40=800 , AB2=106,CA2+CB2=6002+8002=106 ， 则△ABC为直角三角形，AB为斜边，C为直角。北偏东30°和南偏东60°两个方向的夹角是直角。
故答案为：A
4.从电线杆离地面8米处拉一根长为10m的缆绳，这条缆绳在地面的固定点距离电线杆底部有(　　)m．
A．2 B．4 C．6 D．8
【答案】C
【知识点】勾股定理的应用
【解析】【解答】解：由题意得，在Rt△ABC中，

AC＝8，AB＝10，
所以BC＝ 102−82 ＝6．
故答案为：C．
5.如图，池塘边有两点A，B，点C是与BA方向成直角的AC方向上一点，测得CB＝60 m，AC＝20 m，则A，B两点间的距离是(　　)

A．200 m B．40 2 m C．20 10 m D．50 m
【答案】B
【知识点】勾股定理的应用
【解析】【解答】∵CB=60m，AC=20m，AC⊥AB，
∴AB=602−202=402(m) ，
故答案为：B.
6.《九章算术》是我国古代数学的重要著作，其中有一道题，原文是：今有户不知高、广，从之不出二尺，斜之适出，不知其高、宽，有竿，竿比门宽长出4尺；竖放；斜放，竿与门对角线恰好相等问．问门高、宽、对角线长分别是多少？若设门对角线长为x尺，则可列方程（ ）
A．x2＝（x﹣4）2＋（x﹣2）2 B．2x2＝（x﹣4）2＋（x﹣2）2
C．x2＝42＋（x﹣2）2 D．x2＝（x﹣4）2＋22
【答案】A
【分析】
根据题中所给的条件可知，竿斜放就恰好等于门的对角线长，可与门的宽和高构成直角三角形，运用勾股定理可求出门高、宽、对角线长．
【详解】
解：根据勾股定理可得：
x2=（x-4）2+（x-2）2，
故选：A．
7．如图，一艘轮船在处测的灯塔在北偏西15°的方向上，该轮船又从处向正东方向行驶20海里到达处，测的灯塔在北偏西60°的方向上，则轮船在处时与灯塔之间的距离（即的长）为（ ）

A．海里 B．海里
C．40海里 D．海里
【答案】D
【分析】
过作于，解直角三角形求出和，即可解决问题．
【详解】
解：过作于，如图所示：

在中，，海里，
∴（海里），（海里），
∵，，
∴，
∴是等腰直角三角形，
∴海里，
∴海里，
故选：D．
8．《九章算术》是我国古代的数学名著，书中有“折竹抵地”问题：今有竹高一丈，末折抵地，去本三尺．问折者高几何？意思是：一根竹子，原高一丈（一丈尺），一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部尺远，问折断处离地面的高度是多少？设折断处离地面的高度为尺，则可列方程为（ ）
A． B．
C． D．
【答案】D
【分析】
根据勾股定理列方程解答．
【详解】
解：设折断处离地面的高度为尺，则斜边为（10-x）尺，
根据勾股定理得：，
故选：D．
9．如图，一棵大树在一次强台风中于离地面4米处折断倒下，倒下部分与地面成30°夹角，这棵大树在折断前的高度为（ ）

A．6米 B．8米 C．10米 D．12米
【答案】D


由题可知：，，
∴，
∴米；
故答案选D．

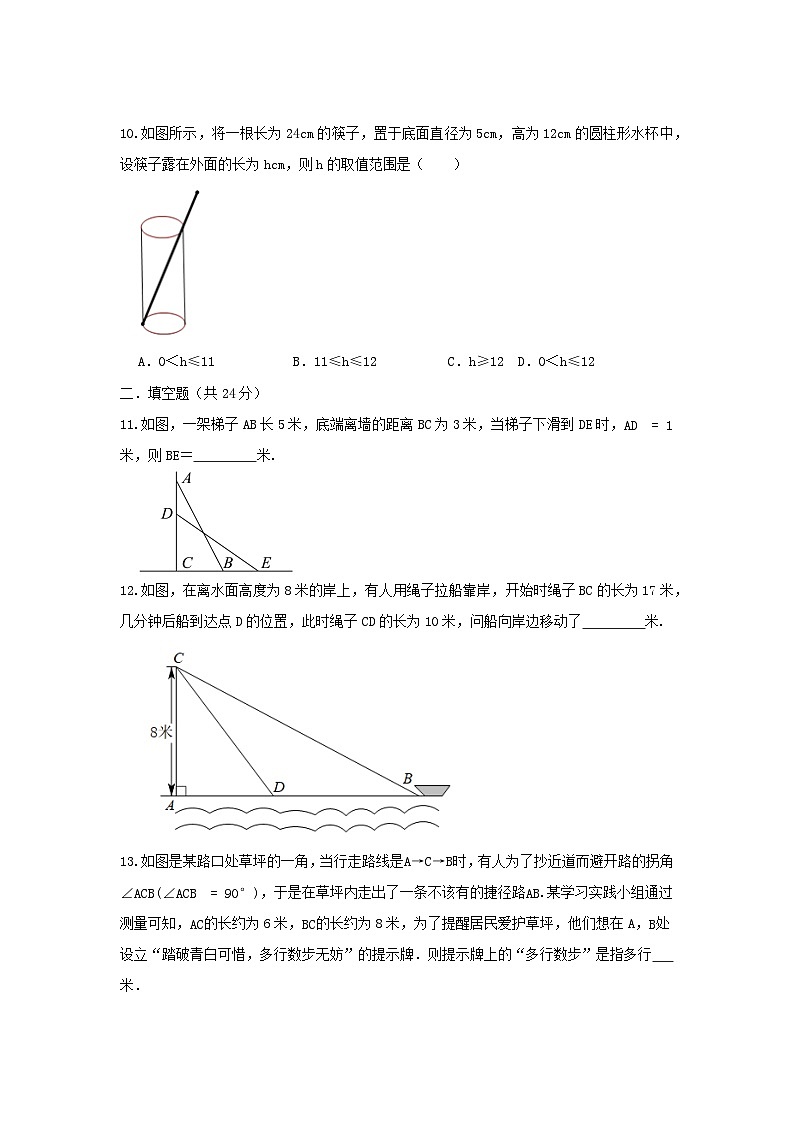
10.如图所示，将一根长为24cm的筷子，置于底面直径为5cm，高为12cm的圆柱形水杯中，设筷子露在外面的长为hcm，则h的取值范围是（　　）

A．0＜h≤11 B．11≤h≤12 C．h≥12 D．0＜h≤12
【答案】B
【知识点】勾股定理的应用
【解析】【解答】解：当筷子与杯底垂直时h最大，h最大＝24﹣12＝12cm．
当筷子与杯底直径及杯高构成直角三角形时h最小，
如图所示：

此时，AB＝ AC2+BC2 ＝ 122+52 ＝13cm，
∴h＝24﹣13＝11cm．
∴h的取值范围是11cm≤h≤12cm．
故答案为：B.
二．填空题（共24分）
11.如图，一架梯子AB长5米，底端离墙的距离BC为3米，当梯子下滑到DE时，AD=1米，则BE＝　 　米.

【答案】1
【知识点】勾股定理的应用
【解析】【解答】解：∵AB=5， BC=3，
∴AC=AB2−BC2=52−32=4，
∵AD＝1，
∴CD=AC-AD=3，
∴CE=DE2−DC2=52−32=4，
∴BE=CE-CB=1米，
故答案为：1.

12.如图，在离水面高度为8米的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为17米，几分钟后船到达点D的位置，此时绳子CD的长为10米，问船向岸边移动了　 　米.

【答案】9
【知识点】勾股定理的应用
【解析】【解答】解：在Rt△ABC中：
∵∠CAB＝90°，BC＝17米，AC＝8米，
∴AB＝BC2−AC2＝172−82＝15（米），
∵CD＝10（米），
∴AD＝CD2−AC2=100−64＝6（米），
∴BD＝AB﹣AD＝15﹣6＝9（米），
答：船向岸边移动了9米，
故答案为：9.
13.如图是某路口处草坪的一角，当行走路线是A→C→B时，有人为了抄近道而避开路的拐角∠ACB(∠ACB=90°)，于是在草坪内走出了一条不该有的捷径路AB.某学习实践小组通过测量可知，AC的长约为6米，BC的长约为8米，为了提醒居民爱护草坪，他们想在A，B处设立“踏破青白可惜，多行数步无妨”的提示牌．则提示牌上的“多行数步”是指多行　 　米．

【答案】4
【知识点】勾股定理的应用
【解析】【解答】解：∵∠ACB=90°，AC的长约为6米，BC的长约为8米，
∴AB=AC2+BC2=10米，
∴AC+BC−AB=4米，
∴多行4米，
故答案为：4．
14.如图，在△ABC中，AB=AC=8，AB的垂直平分线DE分别交AB、AC于点E、 D，BD=BC，△BCD的周长为13，则BC和ED的长分别为　 　.

【答案】5，3
【知识点】线段垂直平分线的性质；勾股定理的应用
【解析】【解答】∵DE是AB的垂直平分线，
∴AD=BD，
∵AC=8，
∴BD+CD=8，
∵△BCD的周长为13，
∴BC=13−8=5,
∵BD=BC，
∴BD=5，
∵DE是AB的垂直平分线，
∴BE=4，∠DEB=90°，
∴DE= 52−42 =3.
15.一个三角形的三边长分别是m2-1，2m，m2+1，则三角形中最大角是　 　?
【答案】90°
【知识点】勾股定理的应用
【解析】【解答】 m2+1显然大于m2-1，又m2+1-2m=(m-1)2≥0，故m2+1为最大边。
而(m2-1)2+(2m)2=4m4+2m2+1=(m2+1)2， 则此为直角三角形，故填90°。
16.如图，有一个长方体的盒子，它的长、宽、高分别是4m，3m和12m，则盒内可放的木棒最长为　 　m.

【答案】13
【知识点】勾股定理的应用
【解析】【解答】解：如图，

长和宽组成的长方形的对角线B’D’= 32+42=5 cm
这根最长的棍子和矩形的高，以及长和宽组成的长方形的对角线组成了直角三角形.
棍子最长为BD= 52+122=13 cm。
故答案为：13。
三． 解答题（共46分）
17.（8分）如图，在笔直的公路AB旁有一座山，为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处，已知点C与公路上的停靠站A的距离为15km，与公路上另一停靠站B的距离为20km，停靠站A、B之间的距离为25km，且CD⊥AB．


（1）求修建的公路CD的长；
（2）若公路CD修通后，一辆货车从C处经过D点到B处的路程是多少？
【答案】（1）解：∵AC=15km，BC=20km，AB=25km，
152+202=252，
∴△ACB是直角三角形，∠ACB=90°，
∵12AC×BC=12AB×CD，
∴CD=AC×BC÷AB=12（km）．
故修建的公路CD的长是12km；
（2）解：在Rt△BDC中，BD= BC2−CD2=16（km），
一辆货车从C处经过D点到B处的路程=CD+BD=12+16=28（km）．
故一辆货车从C处经过D点到B处的路程是28km．

18.（8分）如图，某火车站内部墙面MN上有破损处（看作点A），现维修师傅需借助梯子DE完成维修工作．梯子的长度为5m，将其斜靠在这面墙上，测得梯子底部E离墙角N处3m，维修师傅爬到梯子顶部使用仪器测量，此时梯子顶部D距离墙面破损处1m．

（1）该火车站墙面破损处A距离地面有多高？
（2）如果维修师傅要使梯子顶部到地面的距离为4.8m．那么梯子底部需要向墙角方向移动多少米？
【答案】（1）解：根据题意，得在Rt△DEN中，DE=5m，EN=3m，
由勾股定理，得DN=DE2−EN2=52−32=4(m)．
∵AD=1m，
∴AN=AD+DN=1+4=5(m)．
答：该火车站墙面破损处A距离地面的高度为5m．
（2）解：如图，此时BC是梯子移动后的位置．

∵在Rt△BCN中，BC=5m，CN=4.8m．
∴由勾股定理，得BN=BC2−CN2=52−4.82=75(m)．
∴BE=EN−BN=3−75=85(m)．
答：梯子底部需要向墙角方向移动85m．

19.（10分）如图所示，一辆装满货物的卡车，其外形高2.5米，宽1.6米，要开进厂门形状如图的某工厂，问这辆卡车能否通过该工厂的厂门？

【答案】解：能通过，理由如下：
根据题意可知DH=2.3米．
卡车关于中线对称更容易通过，所以OD=0.8米．
在Rt△OCD中，根据勾股定理，得
CD=OC2−OD2=12−0.82=0.6（米），
∴CH=CD+DH=0.6+2.3=2.9＞2.5，
∴卡车能通过此门．
20.（10分）如图，小明家在一条东西走向的公路北侧米的点处，小红家位于小明家北米（米）、东米（米）点处．

（1）求小明家离小红家的距离；
（2）现要在公路上的点处建一个快递驿站，使最小，请确定点的位置，并求的最小值．
【答案】（1）米；（2）见解析，米
【分析】
（1）如图，连接AB，根据勾股定理即可得到结论；
（2）如图，作点A关于直线MN的对称点A'，连接A'B交MN于点P．驿站到小明家和到小红家距离和的最小值即为A'B，根据勾股定理即可得到结论．
【详解】
解：（1）如图，连接AB，

由题意知AC=500，BC=1200，∠ACB=90°，
在Rt△ABC中，
∵∠ACB=90°，
∴AB2=AC2+BC2=5002+12002=1690000，
∵AB＞0
∴AB=1300米；
（2）如图，作点A关于直线MN的对称点A'，连接A'B交MN于点P．

驿站到小明家和到小红家距离和的最小值即为A'B，
由题意知AD=200米，A'C⊥MN，
∴A'C=AC+AD+A'D=500+200+200=900米，
在Rt△A'BC中，
∵∠ACB=90°，
∴A'B2=A'C2+BC2=9002+12002=2250000，
∵A'B＞0，
∴A'B=1500米，
即从驿站到小明家和到小红家距离和的最小值为1500米．

21.（10分）如图，学校操场边有一块四边形空地ABCD，其中AB⊥AC，AB＝CD＝4m，BC＝9m，AD＝7m．为了美化校园环境，创建绿色校园，学校计划将这块四边形空地进行绿化整理．
（1）求需要绿化的空地ABCD的面积；
（2）为方便师生出入，设计了过点A的小路AE，且AE⊥BC于点E，试求小路AE的长．

【答案】（1）这块空地ABCD的面积是（2+14）m2；（2）AE＝m．
【分析】
（1）先根据勾股定理的逆定理可证明△ACD是直角三角形，根据面积和可得结论；
（2）利用三角形的面积公式求解即可．
【详解】
解：（1）如图，

∵AB⊥AC，
∴∠BAC＝90°，
∵BC＝9，AB＝4，
∴AC＝=，
∵AD＝7，CD＝4，
∴，
∴∠D＝90°，
∴这块空地ABCD的面积＝
=
=
=2+14，
答：这块空地ABCD的面积是（2+14）m2；
（2）∵=，
∴4×＝9×AE，
∴AE＝m．