北师大版九年级上册2 用配方法求解一元二次方程第1课时课后复习题

2　用配方法求解一元二次方程

第1课时

　用配方法求解二次项系数为1的一元二次方程的步骤:

(1)移——移项,使方程左边为二次项和一次项,右边为　常数项　; 

(2)配——配方,方程两边都加上　一次项系数一半　的平方,使原方程变为(x+m)2=n的形式; 

(3)开——如果方程的右边是非负数,即n≥0,就可左右两边开平方得　x+m=±　; 

(4)解——方程的解为x=　-m±　. 

1.利用直接开平方求解一元二次方程时,不要漏掉方程的负根;

2.将方程转化为(x+m)2=n的形式,它的一边是一个完全平方式,另一边是一个常数,当n≥0时,两边开平方便可求出它的根.

1.一元二次方程x2-16=0的根是 (D)

A.x=2   B.x=4   C.x1=2,x2=-2   D.x1=4,x2=-4

2.(2021·甘肃庆阳期中)一元二次方程3(x-2)2-27=0的根是 (C)

A.5   B.-1   C.5或-1   D.3

3.(2021·宁夏中卫期中)一元二次方程x2-6x-1=0配方后可变形为 (B)

A.(x-3)2=8 B.(x-3)2=10 C.(x+3)2=8 D.(x+3)2=10

4.(2021·甘肃兰州模拟)用配方法解方程x2+2x-3=0,下列配方结果正确的是 (D)

A.(x-1)2=2 B.(x-1)2=4 C.(x+1)2=2 D.(x+1)2=4

5.(2021·内蒙古呼和浩特质检)用配方法解下列方程时,配方有错误的是 (B)

A.x2-2x-99=0化为(x-1)2=100 B.x2+8x+9=0化为(x+4)2=25

C.2t2-7t-4=0化为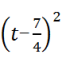= D.3x2-4x-2=0化为=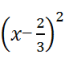

6.若一元二次方程x2+bx+5=0配方后为(x-3)2=k,则b,k的值分别为 (A)

A.-6,4   B.6,4   C.6,13   D.-6,13

7.(2021·新疆乌鲁木齐期中)一元二次方程9(x-1)2-4=0的解是　x1=,x2=　. 

8.(2021·青海海东质检)若一元二次方程(x+6)2=5可转化为两个一次方程,其中一个一次方程是x+6=,则另一个一次方程是　x+6=-　. 

9.(2021·宁夏中卫模拟)将下列各方程写成(x+m)2=n的形式.

(1)x2-2x+1=0.　　　　　(2)x2+8x+4=0.　　　　　(3)x2-x-6=0.

【解析】(1)直接用完全平方公式可得,(x-1)2=0.

(2)移项得,x2+8x=-4,方程两边同时加上16得,x2+8x+16=12,即(x+4)2=12.

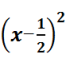(3)移项得,x2-x=6,两边同时加上,得x2-x+=6,即=6.

10.(2021·甘肃定西模拟)解下列方程.

(1)4x2-9=0.　　　　　　　　　　　　　　(2)(x+1)2=16.

【解析】(1)x2=,x=±,所以x1=,x2=-.

(2)x+1=±4,所以x1=3,x2=-5.

1.(2021·宁夏固原模拟)对于方程(ax+b)2=c,下列叙述正确的是 (C)

A.不论c为何值,方程均有实数根 　　　

B.方程的根是x=

C.当c≥0时,方程可化为:ax+b=或ax+b=- 　　　

D.当c=0时,x=

2.小明同学用配方法解方程x2+ax=b2时,方程的两边加上 　. 

3.(2021·内蒙古阿拉善盟期中)用配方法解下列方程.

(1)2x2+3x-1=0.　　　　　　　　(2)(x+3)(x-1)=12.

【解析】(1)移项,化二次项系数为1,得x2+x=,

配方,得x2+x+=+,即=.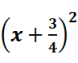

两边开平方,得x+=±,

所以x1=-+,x2=--.

(2)将原方程整理,得x2+2x=15,

两边都加上12,得x2+2x+12=15+12,即(x+1)2=16,

开平方,得x+1=±4,

即x+1=4,或x+1=-4,

∴x1=3,x2=-5.

4.(2021·甘肃庆阳期中)若a为方程(x-)2=16的一正根,b为方程y2-2y+1=13的一负根,求a+b的值.

【解析】∵方程(x-)2=16的解为x=±4,

∵+4>0,-4<0,∴a=+4,

∵方程y2-2y+1=13,

即(y-1)2=13的解为y=1±,

∵1+>0,1-<0,∴b=1-,

则a+b=+4+1-=5.

关闭Word文档返回原板块