中考最值问题课件PPT

这是一份中考最值问题课件PPT，共16页。PPT课件主要包含了胡不归故事导入，练习题，垂线段最短模型等内容，欢迎下载使用。

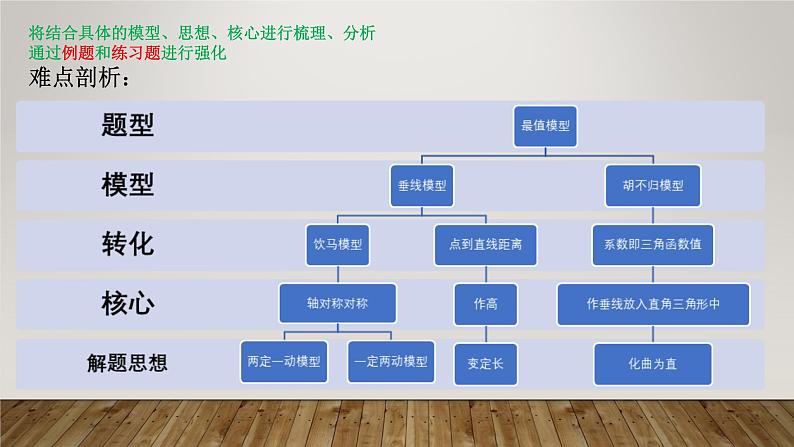
将结合具体的模型、思想、核心进行梳理、分析通过例题和练习题进行强化难点剖析：
话说，从前有一小伙子外出务工，某天不幸得知老父亲病危的消息，便立即赶路回家．小伙子略懂数学常识，考虑到“两点之间线段最短”的知识，就走布满沙石的路直线路径，而忽视了走折线虽然路程多但速度快的实际情况，当赶到家时，老人刚咽了气，小伙子追悔莫及失声痛哭．邻居告诉小伙子说，老人弥留之际不断念叨着“胡不归？胡不归？…”这个问题引起了人们的思索，小伙子能否节省路上时间提前到家？如果可以，他应该选择一条怎样的路线呢？这就是流传千百年的“胡不归问题．
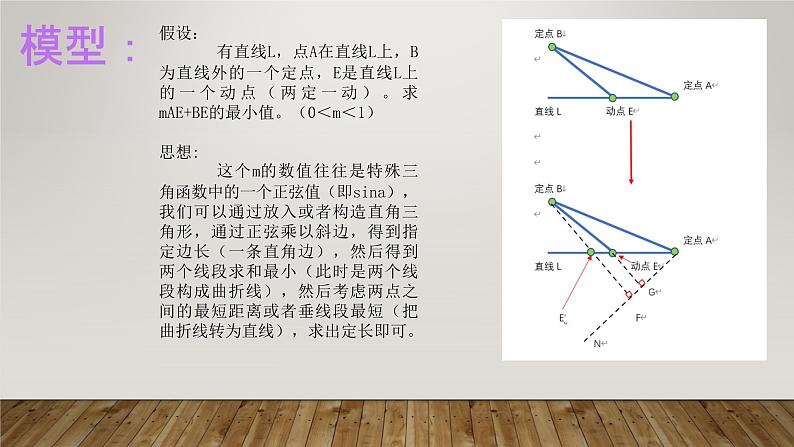
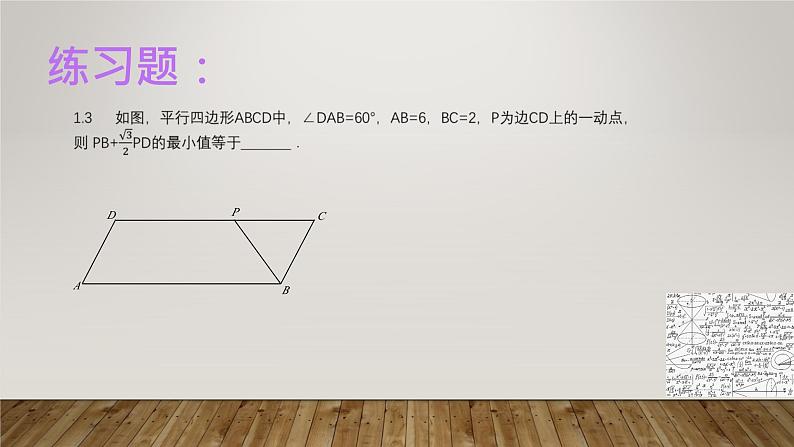
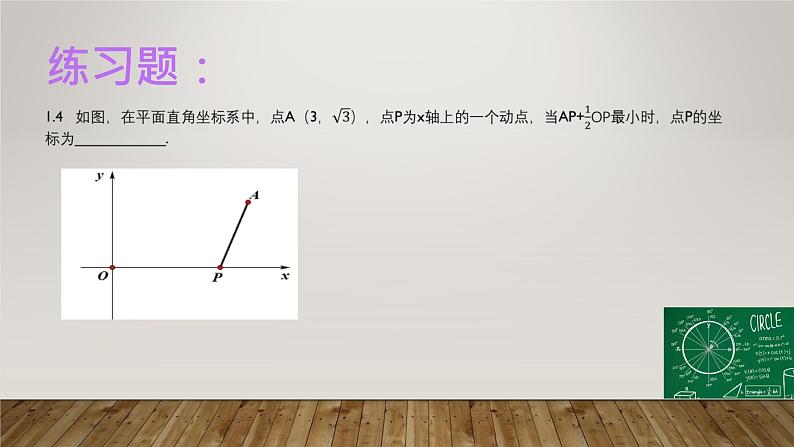
假设： 有直线L，点A在直线L上，B为直线外的一个定点，E是直线L上的一个动点（两定一动）。求mAE+BE的最小值。（0＜m＜1）思想: 这个m的数值往往是特殊三角函数中的一个正弦值（即sina），我们可以通过放入或者构造直角三角形，通过正弦乘以斜边，得到指定边长（一条直角边），然后得到两个线段求和最小（此时是两个线段构成曲折线），然后考虑两点之间的最短距离或者垂线段最短（把曲折线转为直线），求出定长即可。
垂线模型思想：在一个平面内，直线外一点到直线的所有连线中垂线段最短，即最小值。垂线段基础模型：
结论：在这三条连线中，PA作为垂线段最短，亦可从三角形的三边进行推导。拓展：矩形最值边的转换可以从对角线相等作为切入点转换。
垂线最值模型提升模型（饮马模型）饮马模型类型1：一直线、两异侧点假设：有直线L和点A、B，找出E点使得EA+EB最小
原理：两点之间线段最短
2.一直线、两同侧点假设：有直线L和点A、B，找出E点使得EA+EB最小
原理：作A点关于直线L的对称点A‘，A‘与B之间的连线就是两点之间的最短距离，原本的A‘B=A‘E+EB，在对称后AE的长即为A‘E的长。
2.1 如图，在 △ABC 中，AB＝AC＝5，BC 边上高 AD＝4，若点 P 在边 AC 上 ( 不含端点 ) 移动，则 BP 长的最小值为 ________．
当BP⊥AC时，即最短S△ABC=1/2BC×AD =1/2AC×BP∴BP=24/5
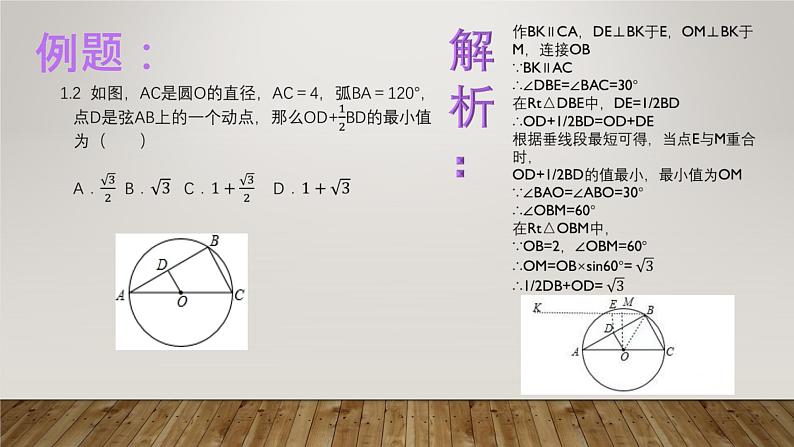
2.2 如图，在△ABC中，AB=10，AC=8，BC=6，经过点C且与边AB相切的动圆与CB，CA分别相交于点E，F，则线段EF长度的最小值是______．
如图：∵∠ACB=90°∴EF是直径设EF的中点为O，圆O与AB的切点为D，连接OD，CO，CD则OD⊥AB∵AB=10，AC=8，BC=6∴OC+OD=EF∴CO+OD＞CD=4.8∵当点O在直角三角形ABC的斜边AB上的高CD时，EF=CD有最小值∴CD=BC×AC÷AB=4.8
2.4 如图，点P是Rt△ABC斜边AB上的一点，PE⊥AC于点E，PF⊥BC于点F，BC=5，AC=12，求线段EF长度的最小值．