2024徐州沛县高三上学期期初模拟测试（一）数学含解析

2024届高三年级上学期期初模拟测试（一）

数学试题

考试时间：120分钟    满分：150分

一、单项选择题：本题共8小题，每小题5分，共40分.在每个小题绐岀的四个选项中，只有一项是符合题目要求的.

1．已知集合，集合，则（    ）

A． B． C． D．

2．已知复数满足，则（    ）

A．1 B． C． D．

3．设，均为锐角，则“”是“”的（    ）

A．充分而不必要条件        B．必要而不充分条件 

C．充分必要条件            D．既不充分也不必要条件

4．某圆锥体积为1，用一个平行于圆锥底面的平面截该圆锥得到一个圆台，若圆台上底面和下底面半径之比为，则该圆台体积为（    ）

A． B． C． D．

5．贯耳瓶流行于宋代，清代亦有仿制，如图所示的青花折枝花卉纹六方贯耳瓶是清乾隆时期的文物，现收藏于首都博物馆，若忽略瓶嘴与贯耳，把该瓶瓶体看作3个几何体的组合体，上面的几何体Ⅰ是直棱柱，中间的几何体Ⅱ是棱台，下面的几何体Ⅲ也是棱台，几何体Ⅲ的下底面与几何体Ⅰ的底面是全等的六边形，几何体Ⅲ的上底面面积是下底面面积的4倍，若几何体Ⅰ、Ⅱ、Ⅲ的高之比分别为，则几何体Ⅰ、Ⅱ、Ⅲ的体积之比为（    ）

A． B． C． D．

6．若，则（    ）

A． B． C． D．1

7．已知在中，，以斜边的中点为圆心，为直径，在点的另一侧作半圆弧，点在圆弧上运动，则的取值范围为（    ）

A． B．

C． D．

8．设，，，则（    ）

A． B． C． D．

二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分

9．已知向量，则下列结论正确的是（    ）.

A． B．

C．向量的夹角为 D．在方向上的投影向量是

10．已知点，若过点的直线交圆：于A，两点，是圆上一动点，则（       ）

A．的最小值为 B．到的距离的最大值为

C．的最小值为 D．的最大值为

11．已知为坐标原点，椭圆.过点作斜率分别为和的两条直线，，其中与交于两点，与交于两点，且，则（    ）

A．的离心率为 B．

C． D．四点共圆

12．已知数列 的项数均为（为确定的正整数，且），若，，则（    ）

A．中可能有项为1 B．中至多有项为1

C．可能是以为公比的等比数列 D．可能是以2为公比的等比数列

三、填空题：本题共4小题，每小题5分，共计20分.

13．数列满足，，则         

14．在三棱锥中，，且，则直线PC与平面ABC所成角的余弦值为          .

15．已知直线与双曲线C：交于点，.为C上一点，且，，则△PAB的面积最大值为          .

16．已知函数是定义在R上的奇函数，当时，恒成立，则m的取值范围是          ．

四、解答题：本题共6小题，共计70分．解答时应写出文字说明、证明过程或演算步骤.

17．已知等差数列和等比数列满足，.

(1)求数列，通项公式

(2)设数列中满足，求和

18．在中，内角A，B，C所对的边分别为a，b，c，且．

(1)求B﹔

(2)若，求的值．

19．中国在第75届联合国大会上承诺，将采取更加有力的政策和措施，力争于2030年之前使二氧化碳的排放达到峰值，努力争取2060年之前实现碳中和(简称“双碳目标”)，此举展现了我国应对气候变化的坚定决心，预示着中国经济结构和经济社会运转方式将产生深刻变革，极大促进我国产业链的清洁化和绿色化．新能源汽车、电动汽车是重要的战略新兴产业，对于实现“双碳目标”具有重要的作用．为了解某一地区电动汽车销售情况，一机构根据统计数据，用最小二乘法得到电动汽车销量y(单位：万台)关于x(年份)的线性回归方程为＝4.7x－9495.2，且销量y的方差，年份x的方差为．

(1)求y与x的相关系数r，并据此判断电动汽车销量y与年份x的相关性强弱；

(2)该机构还调查了该地区100位购车车主性别与购车种类情况，得到的数据如下表：

能否有99%的把握认为购买电动汽车与性别有关?

(3)在购买电动汽车的车主中按照性别进行分层抽样抽取11人，再从这11人中随机抽取4人，记这4人中，男性的人数为X，求X的分布列和数学期望．

参考公式；

(i)线性回归方程：，其中，；

(ii)相关系数：，若r＞0.9，则可判断y与x线性相关较强；

(iii)，其中n＝a＋b＋c＋d．

附表：

20．在四棱锥中，．

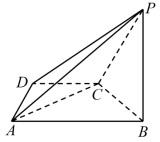
(1)证明：平面平面﹔

(2)若，直线与平面所成的角为，求的长．

21．已知双曲线：的右焦点为，左顶点为A，且，到C的渐近线的距离为1，过点的直线与双曲线C的右支交于P，Q两点，直线AP，AQ与y轴分别交于M，N两点.

(1)求双曲线C的标准方程.

(2)若直线MB，NB的斜率分别为，，判断是否为定值.若是，求出该定值；若不是，请说明理由.

22．已知函数．

(1)若在单调递增，求a的取值范围；公众号：全元高考

(2)当时，，求a的取值范围．