人教版九年级上册24.1.1 圆优质教案设计

教学环节

教师活动

学生活动

设计意图

环节一

创设情境

【观察】

观察下列图形，都有哪些你熟悉的几何图形？

教师PPT展示图片，并提出问题，全班学生回答，学生回答后教师PPT呈现结果.

【交流】

你还能举出生活中常见的圆的例子吗？

预设答案：呼啦圈、井盖、硬币等等.

观察所给图片，根据老师的提问，回答.

 通过观察生活中常见物体的图片，让学生感受圆无处不在，圆中蕴含数学美，激发学生学习兴趣。

环节二

探究新知

【操作】

小学已经对圆有了初步认识，你能说出圆是如何画出来的吗，动手画一画.

预设答案：①用硬币画圆；②用细绳和铅笔画圆；③用圆规画圆.等等… …

教师提出问题，可组织学生动手操作，最后教师动态呈现画圆的过程.

你能试着总结出圆的概念吗？

    教师提出问题，引导学生思考并总结，小组交流探讨后，选代表回答，教师汇总补充：

在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆.

其中，固定的端点O叫做圆心，线段OA叫做半径.

以点O为圆心的圆，记作⊙O，读作“圆O”.

学生动手画图。

可先独立思考，然后小组内交流探讨，尝试总结.

培养学生动手能力，合作意识，使学生在交流与操作中获得知识，培养学生探究意识.

以问题串的形式引发学生自主思考探究，使学生在自主探索，合作交流的过程中完成学习任务.

【探究】

1.（1）以定点O为圆心能画几个圆？

（2）以定长r为半径能画几个圆？

（3）以定点O为圆心，定长r为半径能画几个圆？

预设答案：（1）无数个；（2）无数个；（3）1个

教师引导学生动手画图，得出结论，在此基础上总结出，确定一个圆的条件：

①圆心→确定圆的位置；

②半径→确定圆的大小.

    2.从画圆的过程中你发现了什么？

    预设答案：①圆上各点到定点(圆心O)的距离都等于定长(半径r)；②到定点的距离等于定长的点都在同一个圆上．

    教师引导学生理解并归纳出圆的另一种定义：

    圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r 的点组成的图形．

    在此基础上，教师带领学生对比圆的两种定义：

学生独立思考，先自行尝试画图得出结论，再小组内交流探讨.

组内交流探讨，形成一致结论后，选代表发言

通过探究的3个问题，层层递进，使学生明确确定一个圆需要两个条件，即圆心和半径.同时培养学生的动手能力和探究的意识.

理解圆的另一种定义.

【延伸】

战国时期的《墨经》就有“圆，一中同长也”的记载.

追问：为什么车轮是圆的？

预设答案：当车轮在平面上滚动时，车轮中心与平面的距离不变，因此，坐车的人会感觉到非常平稳.

教师给出《墨经》中对圆的描述，并在此基础上进行追问，最终引导学生从另一个角度归纳出圆的定义.继续追问：

如果车轮做成三角形或四边形的形状，坐车人是什么感觉？

预设答案：颠簸、不平稳.

学生思考并回答.

通过《墨经》中对圆的描述，使学生进一步理解圆的概念.

通过追问，考查学生对知识的掌握情况，培养学生用所学知识解决问题的能力.体现数学来源于生活，又运用于生活.

【探究】

教师提出问题，并展示相关图片，引导学生思考.并适时提出问题追问.

1.圆中还有哪些元素呢？

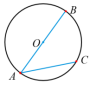
连接圆上任意两点的线段叫做弦. (如图AC)

经过圆心的弦叫做直径. (如图AB)

圆上任意两点间的部分叫做圆弧，简称弧．

以A，C为端点的弧记作；读作“圆弧AC”； 或“弧AC”

圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆．

【辨析】

弦一定是直径吗？直径一定是弦吗？

预设答案：弦不一定是直径，直径一定是弦，且直径是圆中最长的弦.

2.下面两段弧都是以A、C为端点，如何区分呢？

大于半圆的弧叫做优弧. (用三个字母表示)，如：.

小于半圆的弧叫做劣弧.如：.

3.

能够重合的两个圆叫做等圆.

半径相等的两个圆是等圆.反过来，同圆或等圆的半径相等.

在同圆或等圆中，能够重合的弧叫做等弧.

学生结合图形，观察理解并回答.

通过问题串的形式引发学生思考，利用多媒体课件演示相关图形及概念，直观形象，便于学生理解.并通过几个追问，加强学生对圆的相关概念的理解.

【做一做】

教师提出问题，学生思考并抢答.

判断下列说法的正误：

(1)弦是直径；(      )

(2)半圆是弧； (      )

(3)过圆心的线段是直径； (      )

(4)过圆心的直线是直径；(      )

(5)半圆是最长的弧；(      )

(6)半径相等的两个圆是等圆；  (      )

(7)弧是半圆. (      )

答：(1)过圆心的弦才是直径，×；(2)√；

(3)过圆心，且线段的两端点在圆上，这样的线段才是直径，×；

(4)×；(5) ×；(6) √；(7) ×.

学生抢答

巩固圆的相关概念等基础知识，培养学生竞争意识.

环节三 应用新知

【典型例题】

教师提出问题，学生先独立思考，解答.然后再小组交流探讨，教师巡视，如遇到有困难的学生适当点拨，最终教师展示答题过程.

例1：矩形ABCD的对角线AC、BD相交于O.求证：A、B、C、D在以点O为圆心的同一圆上.

证明：∵ABCD是矩形

∴AOOCAC；OBODBD；且ACBD

∴OAOBOCOD

∴A、B、C、D在以O为圆心，以OA为半径的圆上.

学生观察、思考并回答.

通过例题讲解，巩固本节课所学知识. 培养学生解决问题的能力，进一步提高学生分析能力和有条理的表达能力。

环节四 巩固新知

教师给出练习，随时观察学生完成情况并相应指导，最后给出答案，根据学生完成情况适当分析讲解.

1.指出下图中的半径、弦、直径.

答：半径：OA、OB、OC；

弦：AB、BC、AC；

直径：AC.

    2.如果上图中∠AOB60°，则△AOB是           三角形.

答：等边.

3.看图填空：

(1)以A、B为端点的弧有             ；

(2)以B、C为端点的弧有             ；

(3)优弧有                  ；

(4)劣弧有                  ；

答：(1)、；(2)、；

(3)、；(4)、.

4.△ABC中，∠C90°，求证：A、B、C三点在同一圆上.

证明：取AB中点O，连接OC；

∵△ABC中，∠C90°

∴OAOBAB； OCAB

∴OAOBOC

∴A、B、C在以O为圆心，以OA为半径的圆上.

学生自主练习

进一步巩固本节课的内容. 了解学习效果，让学生经历运用知识解决问题的过程，给学生获得成功体验的空间.

环节五 课堂小结

思维导图的形式呈现本节课的主要内容：

学生回顾本节课所学知识，谈收获，体会，师评价.

通过提问让学生回顾、总结、梳理本节课所学内容. 使零散的知识系统化，同时培养学生的语言表达能力.

环节六

布置作业

教科书第81页练习第1、2题.

学生课后自主完成.

通过作业，反馈对所学知识的掌握程度.