初中数学人教版九年级上册25.3 用频率估计概率精品第1课时教学设计

这是一份初中数学人教版九年级上册25.3 用频率估计概率精品第1课时教学设计，共8页。教案主要包含了教学目标，教学重难点，教学用具，教学过程设计等内容，欢迎下载使用。
第二十五章 概率初步
25.3 用频率估计概率
第1课时
一、教学目标
1.能够通过随机试验，获得事件发生的频率；知道通过大量重复试验，可以用频率估计概率；
2.经历利用频率估计概率的过程，让学生了解频率和概率的区别与联系，发展利用频率的集中趋势估计概率的能力；
3.经历抛掷硬币试验和投图钉试验，对数据进行收集、整理、描述与分析，体验频率的随机性与规律性，了解用频率估计概率的合理性和必要性，培养随机观念；
4.通过实验培养学生的数据处理、分析能力以及合作探究精神.
二、教学重难点
重点：理解利用频率估计概率的过程.
难点：了解频率与概率的区别与联系.
三、教学用具
电脑、多媒体、课件
四、教学过程设计
教学
环节
教师活动
学生活动
设计意图
环节一
创设情境
【问题引入】
教师活动：提出问题引导学生思考并用列举法求出概率，再通过追问引出本节课要学习的内容.
问题1：抛掷一枚质地均匀的硬币，硬币落地后会出现哪些可能的结果？

正面向上 反面向上
问题2：“正面向上”和“反面向上”的概率分别是多少？
答案：都是0.5
追问：抛掷一枚硬币50次，一定会有25次“正面向上”和25次“反面向上”吗？






在教师的引导下认真思考




通过熟悉的抛硬币试验提出问题，激起学生思考，激发学生探求新知的渴望.
环节二 探究新知
【合作探究】
教师活动：先给出探究问题，学生分组探究，并展示实验数据和过程，最后用课件展示参考过程.
探究问题：请同学们分组进行抛掷硬币试验，每组抛掷一枚硬币50次，统计“正面向上”出现的频数，计算频率(结果保留小数点后两位)，并完成下面的表格.


展示过程：

根据表中的数据，在下图中标注出对应的点.

【思考】
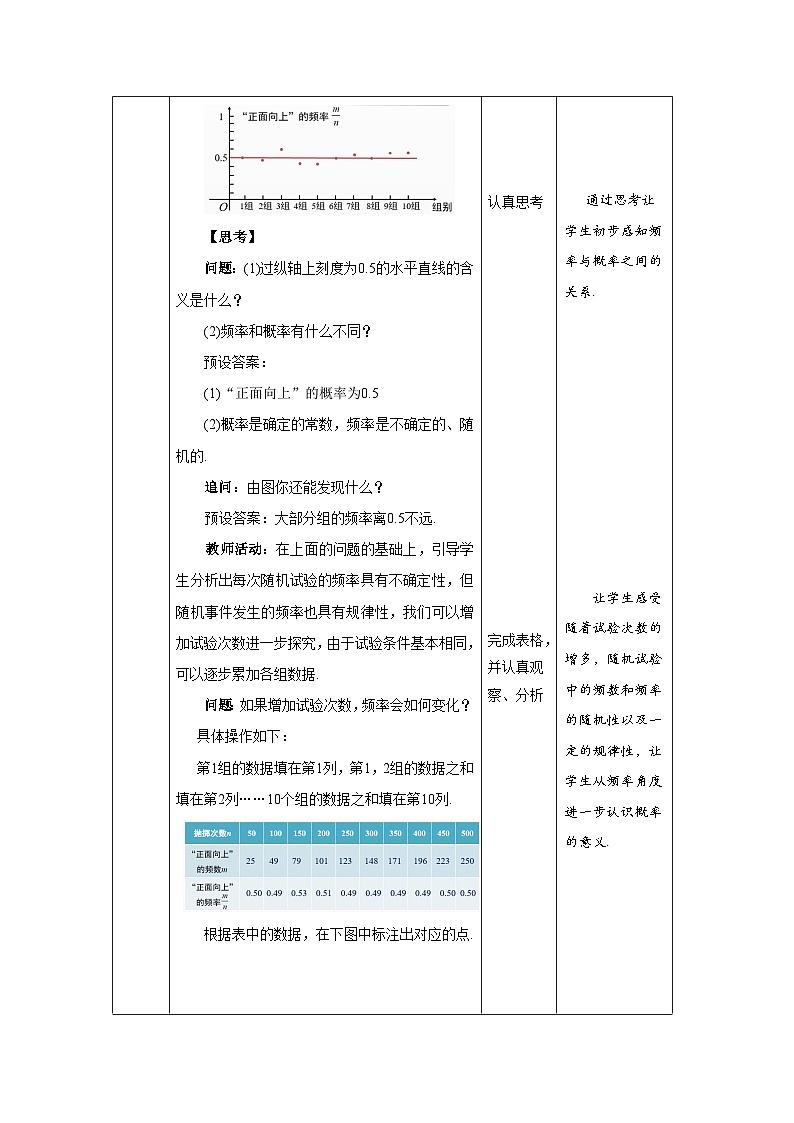
问题：(1)过纵轴上刻度为0.5的水平直线的含义是什么？
(2)频率和概率有什么不同？
预设答案：
(1)“正面向上”的概率为0.5
(2)概率是确定的常数，频率是不确定的、随机的.
追问：由图你还能发现什么？
预设答案：大部分组的频率离0.5不远.
教师活动：在上面的问题的基础上，引导学生分析出每次随机试验的频率具有不确定性，但随机事件发生的频率也具有规律性，我们可以增加试验次数进一步探究，由于试验条件基本相同，可以逐步累加各组数据.
问题：如果增加试验次数，频率会如何变化？
具体操作如下：
第1组的数据填在第1列，第1，2组的数据之和填在第2列……10个组的数据之和填在第10列.

根据表中的数据，在下图中标注出对应的点.

【观察】
问题：随着试验次数的增多，“正面向上”的频率有什么规律？
预设答案：“正面向上”的频率在0.5左右摆动，随着抛掷次数的增加，在0.5左右摆动的幅度越来越小.
问题：历史上，有些人曾做过成千上万次抛掷硬币的试验，一些试验结果如下表，由表观察“正面向上”的频率的变化趋势是什么？

随着抛掷次数的增加，频率呈现出一定的稳定性：在0.5附近摆动的幅度越来越小.
我们称“正面向上”的频率稳定于0.5.它与用列举法得出的“正面向上”的概率是同一个数值.
【归纳】
对一般的随机事件，在做大量重复试验时，随着试验次数的增加，一个事件出现的频率，总在一个固定数的附近摆动，显示出一定的稳定性.
我们可以通过大量重复试验，用一个随机事件发生的频率去估计它的概率.
【拓展】

雅各布·伯努利1654年出生于瑞士巴塞尔，1705年卒于同地.最初遵从父亲的意见学神学，后来兴趣转向数学.他的遗著《猜度术》于1713年出版，书中对频率的稳定性规律进行了严格的证明，阐述了“频率稳定于概率”.
【想一想】
教师活动：先学生思考30秒，再抢答，最后给出答案.
判断正误：
(1)连续掷一枚质地均匀硬币10次，结果10次全部是正面，则正面向上的概率是1.
(2)小明掷硬币10000次，则正面向上的频率在0.5附近.
(3)某彩票的中奖率是，那么买1000张彩票就一定能中奖.
答案：(1)×；(2)√；(3)×.
【归纳】
频率与概率的区别与联系












分组探究交流，并做好记录























认真思考

















完成表格，并认真观察、分析



















认真观察并思考












明确利用频率估计概率的方法

















思考并抢答












熟悉频率与概率的区别与联系








通过分组探究的形式让学生经历数据的收集、整理、描述与分析的过程，发展学生的数据分析观念，同时提高学生的合作交流意识.













通过思考让学生初步感知频率与概率之间的关系.









让学生感受随着试验次数的增多，随机试验中的频数和频率的随机性以及一定的规律性，让学生从频率角度进一步认识概率的意义.










通过历史数据进一步验证实验次数增加时，频率的变化趋势.









通过归纳总结强调利用频率估计概率的方法.




通过拓展资料进一步验证利用频率估计概率的方法的合理性.






通过抢答进一步熟悉频率和概率的关系，并为后面总结频率与概率的区别和联系作铺垫.





通过归纳总结培养学生的归纳概括能力.

环节三
应用新知
【典型例题】
【例】从一定高度抛掷一枚图钉，估计出“钉尖向上”的概率.(要求：设计一个试验，用频率估计概率)

解：试验参考过程如下：
每组同学投一枚图钉50次，第1组的数据填在第1列，第1，2组的数据之和填在第2列……10个组的数据之和填在第10列.
根据表格数据在下图中标注点.

频率稳定在0.56附近，所以，“钉尖向上”的概率为0.56.
【延伸】
教师活动：教师提出问题，引导学生思考，分析出利用频率估计概率的方法不受“各种结果出现的可能性相等”的限制.
问题：能用列举法求上述随机事件的概率吗？
预设答案：“钉尖向上”、“钉尖向下”出现的可能性不相等，所以不能用列举法求上述随机事件的概率.
结论：列举法求概率仅适用于“各种结果出现的可能性相等”的随机事件，用频率估计概率不受这个条件限制.








明确本题的做法

























在教师的引导下认真思考





让学生在探究过程中进一步加深对利用频率估计概率的方法的认识和理解，培养学生的应用意识，并发展利用频率的集中趋势估计概率的能力.













通过延伸的问题让学生明白两种求概率的方法的适用条件，进一步感知利用频率估计概率的必要性.
环节四
巩固新知
【随堂练习】
1.在大量重复试验中，关于随机事件发生的频率与概率，下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的，与频率无关
D.随着试验次数的增加，频率一般会越来越接近概率
2.运用乘法公式计算：
下表记录了一名球员在罚球线上投篮的结果.

(1)计算投中频率(结果保留小数点后两位)；
(2)这名球员投篮一次，投中的概率约是多少(结果保留小数点后一位)？
3.如图显示了用计算机模拟随机投掷一枚
图钉的某次试验的结果.下面有三个推断，其中合理的是( )

①当投掷次数是500时，计算机记录“钉尖
向上”的次数是308，所以“钉尖向上”的概率是0.616；
②随着试验次数的增加，“钉尖向上”的频
率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618；
③若再次用计算机模拟此试验，则当投掷
次数为1 000时，“钉尖向上”的概率一定是0.620.
A.① B.② C.①② D.①③
答案：
1. D
2.解：(1) 0.56；0.60；0.52；0.52 ；0.49；0.51；0.50.
(2) 投中的概率约是0.5.
3.B






自主完成练习，然后集体交流评价.




通过课堂练习及时巩固本节课所学内容，并考查学生的知识应用能力，培养独立完成练习的习惯.

环节五
课堂小结






回顾本节课所讲的内容

通过小结总结回顾本节课学习内容，帮助学生归纳、巩固所学知识.
环节六
布置作业

教科书第144页
练习第2题
第147页
习题25.3第3题



课后完成练习
通过课后作业，教师能及时了解学生对本节课知识的掌握情况，以便对教学进度和方法进行适当的调整.