




初中数学北师大版九年级上册2 矩形的性质与判定优秀一课一练
展开北师大版数学九上 第一章1.2 矩形的性质与判定测试卷 B卷
一,选择题(共30分)
1.折叠矩形纸片ABCD,使点B落在点D处,折痕为MN,已知AB=8,AD=4,则MN的长是( )
A. B.2 C. D.4
【答案】B
【分析】
连接BM,利用折叠的性质证明四边形BMDN为菱形,设DN=NB=x,在RtABD中,由勾股定理求BD,在RtADN中,由勾股定理求x,利用菱形计算面积的两种方法,建立等式求MN.
【详解】
解:如图,连接BM,
由折叠可知,MN垂直平分BD,
又AB∥CD,
∴BON≌DOM,
∴ON=OM,
∴四边形BMDN为菱形(对角线互相垂直平分的四边形是菱形),
设DN=NB=x,则AN=8﹣x,
在RtABD中,由勾股定理得:BD==,
在RtADN中,由勾股定理得:AD2+AN2=DN2,
即42+(8﹣x)2=x2,
解得x=5,
根据菱形计算面积的公式,得
BN×AD=×MN×BD,
即5×4=×MN×,
解得MN=.
故选:B.
2.如图,在矩形中,分别是的中点,若,则的长是( )
A.4 B. C. D.
【答案】D
【分析】
结合矩形的性质,勾股定理,利用证明,进而可求解.
【详解】
解:四边形为矩形,,,
,,,,
,
为的中点,
,
,
,
点为的中点,
,
,
在△DAF和△AEB中,
,
.
故选:D.
3.下列命题是真命题的是( ).
A.正六边形的外角和大于正五边形的外角和 B.正六边形的每一个内角为
C.有一个角是的三角形是等边三角形 D.对角线相等的四边形是矩形
【答案】B
【分析】
根据多边形外角和、正多边形内角和、等边三角形、矩形的性质,对各个选项逐个分析,即可得到答案.
【详解】
正六边形的外角和,和正五边形的外角和相等,均为
∴选项A不符合题意;
正六边形的内角和为:
∴每一个内角为,即选项B正确;
三个角均为的三角形是等边三角形
∴选项C不符合题意;
对角线相等的平行四边形是矩形
∴选项D不正确;
故选:B.
4.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,若旋转角为20°,则∠1为( )
A.110° B.120° C.150° D.160°
【详解】
设C′D′与BC交于点E,如图所示:
∵旋转角为20°,
∴∠DAD′=20°,
∴∠BAD′=90°−∠DAD′=70°.
∵∠BAD′+∠B+∠BED′+∠D′=360°,
∴∠BED′=360°−70°−90°−90°=110°,
∴∠1=∠BED′=110°.
故选:A.
5.如图,四边形ABCD是矩形,连接BD,,延长BC到E使CE=BD,连接AE,则的度数为( )
A. B. C. D.
【详解】
如图,连接AC.
∵四边形ABCD是矩形,∴AC=BD.
∵EC=BD,∴AC=CE,∴∠AEB=∠CAE,易证∠ACB=∠ADB=30°.
∵∠ACB=∠AEB+∠CAE,∴∠AEB=∠CAE=15°.
故选A.
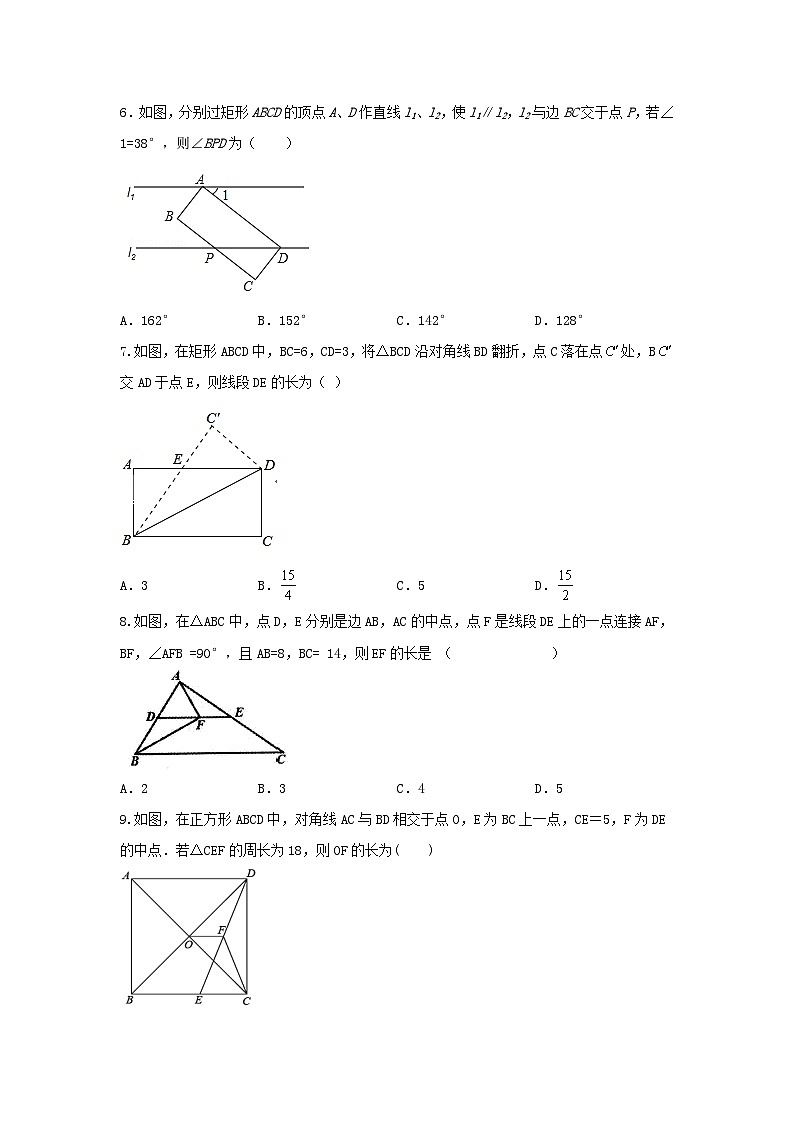
6.如图,分别过矩形ABCD的顶点A、D作直线l1、l2,使l1∥l2,l2与边BC交于点P,若∠1=38°,则∠BPD为( )
A.162° B.152° C.142° D.128°
【详解】
解:∵l1∥l2,∠1=38°,∴∠ADP=∠1=38°,∵矩形ABCD的对边平行,∴∠BPD+∠ADP=180°,∴∠BPD=180°﹣38°=142°,故选C.
7.如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点处,B交AD于点E,则线段DE的长为( )
A.3 B. C.5 D.
【详解】
解:设ED=x,则AE=6-x,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠EDB=∠DBC;
由题意得:∠EBD=∠DBC,
∴∠EDB=∠EBD,
∴EB=ED=x;
由勾股定理得:
BE2=AB2+AE2,
即x2=9+(6-x)2,
解得:x=,
∴ED=.
故选:B.
8.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点连接AF,BF,∠AFB =90°,且AB=8,BC= 14,则EF的长是 ( )
A.2 B.3 C.4 D.5
【详解】
解:∵∠AFB=90°,点D是AB的中点,
∴DF= AB=4,
∵BC= 14,D、E分别是AB,AC的中点,
∴DE=BC=7,
∴EF=DE-DF=3,
故选:B
9.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为( )
A.3 B.4 C. D.
【详解】
∵CE=5,△CEF的周长为18,
∴CF+EF=18-5=13.
∵F为DE的中点,
∴DF=EF.
∵∠BCD=90°,
∴CF=DE,
∴EF=CF=DE=6.5,
∴DE=2EF=13,
∴CD=,
∵四边形ABCD是正方形,
∴BC=CD=12,O为BD的中点,
∴OF是△BDE的中位线,
∴OF=(BC-CE)=(12-5)=3.5,
故选D.
10.如图,平面直角坐标系中,长方形OABC,点A,C分别在x轴,y轴的正半轴上,点B(6,3),现将△OAB沿OB翻折至△OA′B位置,OA′交BC于点P.则点P的坐标为( )
A.(,3) B.(,3) C.(,3) D.()
【详解】
∵将△OAB沿OB翻折至△OA′B位置,OA′交BC于点P,
∴∠A'OB=∠AOB,
∵四边形OABC是矩形,
∴BC∥OA,
∴∠OBC=∠AOB,
∴∠OBC=∠A'OB,
∴OP=BP,
∵点B的坐标为(6,3),
∴AB=OC=3,OA=BC=6,
设OP=BP=x,则PC=6﹣x,
在Rt△OCP中,根据勾股定理得,OC2+PC2=OP2,
∴32+(6﹣x)2=x2,
解得:x=,
∴PC=6﹣=,
∴P(,3),
故选:A.
二. 填空题(共24分)
11.在矩形ABCD中,作∠B的平分线交直线AD于点E,则∠BED是 度.
【答案】45或135
【知识点】矩形的性质;角平分线的定义
【解析】【解答】解:∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,
∵BE平分∠ABC,
∴∠ABE=∠CBE=45°,
由题意可分:
①当∠B的平分线交线段AD于点E,如图所示:
∴∠BED=180°−∠CBE=135°;
②当∠B的平分线交线段AD外于点E,如图所示:
∴∠BED=∠CBE=45°;
综上所述:∠BED=135°或45°;
故答案为45或135.
12.如图,在矩形ABCD中,AB=3,对角线AC的长为5,作AC的垂直平分线交BC于点M,连接AM,则△ABM的周长为 .
【答案】7
【知识点】线段垂直平分线的性质;勾股定理;矩形的性质
【解析】【解答】解:∵四边形ABCD是矩形,
∴∠B=90°,
∴BC=AC2−AB2=25−9=4,
∵AC的垂直平分线交BC于点M,
∴AM=CM,
∴△ABM的周长=AB+BM+AM=AB+BC=7
故答案为:7.
13.如图,在矩形ABCD中,AB=5,AD=6,AE=2,将△ABE沿BE翻折,使点A落在点A′处,作射线EA′,交BC的延长线于点F,则CF的长为 .
【答案】54
【知识点】平行线的性质;等腰三角形的判定;勾股定理;矩形的性质;翻折变换(折叠问题)
【解析】【解答】解:∵在矩形 ABCD 中, AD∥BC , AD=BC ,
∴∠AEB=∠EBC ,
∵根据折叠有: ∠AEB=∠A′EB , AE=A′E , AB=A′B , ∠EAB=∠EA′B=90° ,
∴∠A′EB=∠EBC ,
∴EF=BF ,
∵AB=5 , AD=6 , AE=2 ,
∴A′B=5 , EF=EA′+A′F=BF=BC+CF ,
∴A′F=BC+CF−EA′=4+CF , BF=BC+CF=6+CF ,
∵∠EA′B=90° ,
∴在 Rt△FA′B 中, BF2=A′B2+A′F2 ,
∴(6+CF)2=52+(4+CF)2 ,
解得: CF=54 ,
故答案为: 54 .
14.如图,在矩形ABCD中,对角线AC,BD交于点O,若OA=2,则BD= .
【答案】4
【知识点】矩形的性质
【解析】【解答】解:∵矩形ABCD,
∴BD=AC=2OA=4.
故答案为:4
15.如图,BE,BF分别是∠ABC与它的邻补角∠ABD的平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F,EF分别交边AB,AC于点M和N.若AB=7,BC=4,则MF+NE的长为 .
【答案】5
【知识点】等腰三角形的性质;矩形的判定与性质;角平分线的定义;三角形的中位线定理
【解析】【解答】解:∵BE,BF分别是∠ABC与它的邻补角∠ABD的平分线,
∴∠ABC=2∠ABE,∠ABD=2∠ABF,∠ABE=∠EBC,
∵∠ABC+∠ABD=180°,
∴2∠ABF+2∠ABE=180°
∴∠ABF+∠ABE=∠FBE=90°
∵AE⊥BE,AF⊥BF,
∴∠AFB=∠AEB=90°,
∴四边形AFBE是矩形,
∴EF=AB=7,MB=ME,
∴∠ABE=∠MEB,
∴∠MEB=∠EBC,
∴ME∥BC,
∵MB=MA,
∴AN=NC,
∴MN是△ABC的中位线,
∴MN=12BC=2,
∴MF+NE=EF−MN=5.
故答案为:5
16.如图所示,已知矩形 ABCD 中, AD=10 , AB=6 现将边 AD 绕它的一个端点旋转,当另一端点恰好落在边 BC 所在直线的点E处时,线段 DE 的长度为
【答案】210 或 610 或10
【知识点】勾股定理;矩形的性质
【解析】【解答】解:如图,
∵四边形ABCD是矩形,
∴AB=CD=6,AD=BC=10,∠ABC=∠DCB=90°,
当AD=AE=10时,BE= AE2−AB2=102−62=8 ,
∴DE1= CD2+E1C2=62+22=210 ,DE2= CD2+E2C2=62+182=610 ,
当DE=DA=10时,DE=10,
综上所述,满足条件的DE的值为 210 或 610 或 10 .
故答案为: 210 或 610 或10.
三. 解答题(共46分)
17.(8分).如图,在▱ABCD中,各内角的平分线相交于点E,F,G,H.
(1)求证:四边形EFGH是矩形;
(2)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.
【详解】
(1)∵GA平分∠BAD,GB平分∠ABC,∴∠GAB∠BAD,∠GBA∠ABC.
∵▱ABCD中,∠DAB+∠ABC=180°,∴∠GAB+∠GBA(∠DAB+∠ABC)=90°,即∠AGB=90°,同理可得:∠DEC=90°,∠AHD=90°=∠EHG,∴四边形EFGH是矩形;
(2)依题意得:∠BAG∠BAD=30°.
∵AB=6,∴BGAB=3,AG=3CE.
∵BC=4,∠BCF∠BCD=30°,∴BFBC=2,CF=2,∴EF=3,GF=3﹣2=1,∴矩形EFGH的面积=EF×GF.
18.(8分)已知,如图1,在中,,是边上的中线,是的中点,过点作交的延长线于点,连接.
(1)求证:四边形是菱形;
(2)如图2,连接,若,在不添加任何辅助性的情况下,请直接写出长度等于的所有线段.
【答案】(1)见解析;(2)长度等于的所有线段是,,,,.
【分析】
(1)先证△CDE≌△FAE(ASA),得CD=FA,再由直角三角形斜边上的中线性质得AD=BC=CD=BD,则BD=FA,且BD∥FA,即可得出结论;
(2)证△ABC、△ACD、△ABD都是等腰直角三角形,得AD=CD=AC=AB=BD,再由菱形的性质得AF=BF=AD=BD=AC即可.
【详解】
解:(1)证明:∵AF∥BC,
∴∠CDE=∠FAE,
∵E是AD的中点,
∴DE=AE,
在△CDE和△FAE中,
,
∴△CDE≌△FAE(ASA),
∴CD=FA,
∵∠CAB=90°,AD是BC边上的中线,
∴AD=BC=CD=BD,
∴BD=FA,且BD∥FA,
∴四边形ADBF是平行四边形,
又∵AD=BD,
∴平行四边形ADBF是菱形;
(2)解:长度等于AC的所有线段为AD、CD、BD、AF、BF,理由如下:
∵CE=BE,AD是BC边上的中线,
∴AD⊥BC,
∴AD垂直平分BC,
∴AB=AC,
∴△ABC、△ACD、△ABD都是等腰直角三角形,
∴AD=CD=AC=AB=BD,
由(1)得:四边形ADBF是菱形,
∴AF=BF=AD=BD=AC,
即长度等于AC的所有线段为AD、CD、BD、AF、BF.
19.(10分)在一些几何问题中直接求证或求解有些困难,若能正确添加辅助线,问题就迎刃而解了.
(1)证明:三角形中位线定理.
已知:如图1,是的中位线.
求证:________________________________.
证明:如图1,在中,延长到点F,使得,连接.请继续完成证明过程.
(2)如图2在矩形中,,E为边的中点,G为边上的点,且,,求矩形的面积.
【答案】(1),证明见解析;(2)
【分析】
(1)利用“SAS”证明△ADE和△CEF全等,根据全等三角形对应边相等可得AD=CF,然后判断四边形BCFD是平行四边形,根据平行四边形的性质可证得;
(2)先判断出,进而判断出EC垂直平分GH,再用勾股定理,即可得出结论.
【详解】
(1)填:,
证明:如图,延长DE到点F,使得EF=DE,连接CF;
在△ADE和△CFE中:
∴ ,
∴∠A=∠ECF,AD=CF,
∴ ,
又∵AD=BD,
∴CF=BD,
∴四边形BCFD是平行四边形,
∴;
(2)如图,延长GE,CD交于一点H,
∵E为AD中点,
∴AE=ED,且∠A=∠EDH=90°,
在和中,
∴(ASA),
∴,
∵∠GEC=90°,
∴CE垂直平分GH,
∴GC=HC=DH+CD=4,
在Rt△GBC中,已知GC=4,GB=CD-AG=3-1=2,
∴,
∴矩形面积= .
20.(10分)如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC.
(1)求证:四边形AECD是菱形;
(2)过点E作EF⊥CD于点F,若AB=3,BC=5,求EF的长.
【答案】(1)证明见解析;(2).
【分析】
(1)在直角三角形ACB中,E是斜边BC的中点,可得AE = CE;由AD∥BC,AE∥DC可得四边形AECD是平行四边形;再根据邻边相等的平行四边形是菱形,即可完成本题的证明;
(2)过点A作AG⊥BC于点G,在直角三角形ACB中,由勾股定理可得AC = 4,再根据等积法易得AG=;S菱形AECD = CD·EF = CE·AG,而CD = CE,从而可得EF = AG,即可得出本题答案.
【详解】
(1)∵∠BAC=90°,E是BC的中点,
∴AE =BC = CE,
又∵AD∥BC,AE∥DC,
∴四边形AECD是平行四边形;
∴四边形AECD是菱形.
(2)过点A作AG⊥BC于点G
在直角三角形ACB中,
,
,
∵AB=3,BC=5,
∴AG=;
又∵S菱形AECD = CD·EF = CE·AG,CD = CE,
∴EF = AG = .
21.(10分)如图,在直角坐标系中,点O是坐标原点,四边形OABC是平行四边形,,点A的坐标为,点B的坐标为.动点P从点O出发,沿射线OA方向以每秒1个单位的速度匀速运动;动点Q同时从点A出发,到达点B之后,继续沿射线BC运动,以每秒2个单位的速度匀速运动,设点P运动的时间为t秒().
(1)写出点C的坐标;当运动2秒时,求的面积.
(2)在整个运动过程中,是否存在这样的t,使以A,P,Q,C为顶点的四边形是矩形?若存在,请求出t的值,若不存在,请改变点P的运动速度,使以A,P,Q,C为顶点的四边形是矩形,求出此时点P的速度.
(3)在整个运动过程中,t为何值时,以A,P,Q,C为顶点的四边形是平行四边形?
【答案】(1)C,;(2)不存在,点P的速度为每秒个单位;(3)s或8s
【分析】
(1)利用平行四边形的性质可得点C坐标,作QE⊥x轴于E,BF⊥x轴于F.求出PA.QE即可得到的面积.
(2)画出以点A、P、Q、C为顶点的四边形是矩形时的图像,求出此时点P和点Q运动的时间,再判断,从而求出点P应有的速度;
(3)当点Q在射线BC上时,CQ=PA时,A,P,Q,C为顶点的四边形是平行四边形.由此构建方程即可解决问题.
【详解】
解:(1)∵四边形OABC是平行四边形,
∴OA=BC=6,BC∥OA,
∵B,
∴C,
如图,作QE⊥x轴于E,BF⊥x轴于F.
∵A(6,0),B,
∴OA=6,OF=10,BF=,
∴AF=10-6=4,AB==8,
当t=2时,OP=2,PA=4,AQ=4,
∵四边形OABC是平行四边形,
∴∠BAF=∠COA=60°,
∵QE⊥AE,
∴∠AEQ=90°,
∴AE=AQ=2,
∴EQ==,
∴S△PAQ=•PA•EQ=×4×=;
(2)如果以点A、P、Q、C为顶点的四边形是矩形,如图,
此时OP=4,则t=4,
AB+BQ=8+4=12,则t=6,
∴不存在这样的t,
若改变点P的运动速度,则为;
(3)如图,当点Q在射线BC上时,CQ=PA时,A,P,Q,C为顶点的四边形是平行四边形.
∴|14-2t|=|t-6|,
解得t=或8,
∴t为s或8s时,以A,P,Q,C为顶点的四边形是平行四边形.
初中数学北师大版九年级上册2 矩形的性质与判定综合训练题: 这是一份初中数学北师大版九年级上册2 矩形的性质与判定综合训练题,共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中数学北师大版九年级上册2 矩形的性质与判定课时作业: 这是一份初中数学北师大版九年级上册2 矩形的性质与判定课时作业,共9页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学北师大版九年级上册第一章 特殊平行四边形2 矩形的性质与判定课时训练: 这是一份初中数学北师大版九年级上册第一章 特殊平行四边形2 矩形的性质与判定课时训练,共7页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。













