

2023年辽宁省鞍山市铁东区小升初数学试卷(含解析)
展开2023年辽宁省鞍山市铁东区小升初数学试卷
一、填空题(每2题6分,其余每题各2分,共24分)
1. 我们生活的地球天文年龄大约为4550000000年,这个数读作______ 亿年,把这个数改写成用“万”作单位的数是______ 万年。
2. 6÷ ______ =3:5=15=( )______ %= ______ 成
3. 你知道成语“南辕北辙”吗?它的意思是心想往南走,而车子却向北行驶。如果将车子向南行驶10km记作+10km,那么−20km表示______ 。
4. 如图把平行四边形分成一个梯形和一个三角形。梯形面积是______ cm2,三角形面积是______ cm2,平行四边形面积是______ cm²。
5. 三角形三个内角度数的比是1:1:2,这个三角形是 三角形。
6. 14+14+14+12= ______ ×5
7. 从5里面连续减去______ 个0.5结果是0。
8. 李老师在实验室里把8L药水倒入如图的两个容器中,刚好都倒满.已知圆柱形和圆锥形容器的底面积相等,则圆柱形容器的容积是______ L,圆锥形容器的容积是______ L.
9. 一幅图的比例尺是。图上的1cm表示实际距离______ km,实际距离50km在图上要画______ cm。把这个线段比例尺改写成数值比例尺是______ 。
10. 我国苗族的千人长桌宴是苗族宴席的最高形式,这项礼仪文化已有几千年的历史。如图1张桌子可以坐6人,2张桌子可以坐10人。照这样的规律摆下去:
3张桌子可以坐______ 人;n张桌子可以坐______ 人。
二、选择题(每小题2分,共20分)
11. 把一根细铁丝剪成三段,围成一个三角形,下面剪法能围成三角形的是( )
A.
B.
C.
D.
12. 如图三组图形中,每组中的两个图形的运动方式分别是( )
A. 平移、旋转、轴对称 B. 平移、旋转、旋转
C. 平移、轴对称、轴对称 D. 平移、轴对称、旋转
13. 著名的哥德巴赫猜想被誉为“数学皇冠上的明珠”。这个猜想的内容是“任意一个大于2的偶数都可以写成两个质数之和”。下面符合这个猜想。( )
A. 6=1+5 B. 28=11+17 C. 54=3+51 D. 96=5+91
14. 如图A、B、C三岛的位置构成了一个直角三角形。A岛的位置在B岛的( )
A. 北偏东60°方向,距离4km
B. 南偏西30°方向,距离4km
C. 南偏西60°方向,距离4km
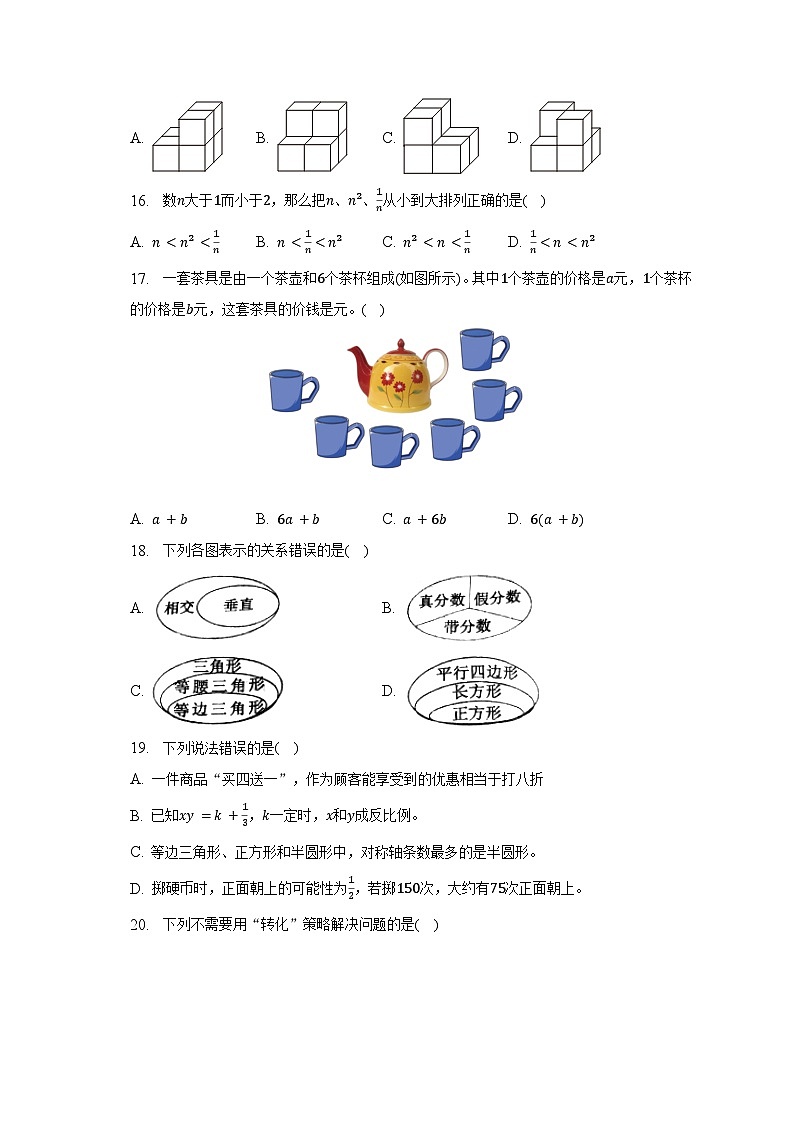
15. 用6个同样的正方体拼成一个立体图形,从正面、上面和左面看到的形状完全一样,这个立体图形是( )
A. B. C. D.
16. 数n大于1而小于2,那么把n、n²、1n从小到大排列正确的是( )
A. n
A. a+b B. 6a+b C. a+6b D. 6(a+b)
18. 下列各图表示的关系错误的是( )
A. B.
C. D.
19. 下列说法错误的是( )
A. 一件商品“买四送一”,作为顾客能享受到的优惠相当于打八折
B. 已知xy=k+13,k一定时,x和y成反比例。
C. 等边三角形、正方形和半圆形中,对称轴条数最多的是半圆形。
D. 掷硬币时,正面朝上的可能性为12,若掷150次,大约有75次正面朝上。
20. 下列不需要用“转化”策略解决问题的是( )
A. 计算:1.2×1.5→12×15÷100 12+13→36+26 12÷23→12×32
B. 画对称轴图形
C. 推导圆柱的体积公式
三、计算题(共12分)
21. 解方程。(6分)
x−0.25=13
3.6x=32.5
23x−12x=512
22. 脱式计算。 (6分)
125×88
75.6+57+24.4+27
13.76−712−1.76−512
(7.5×3.14)÷(6.28×2.5)
3.75×8.8+62.5×0.88
48×(1112−34+16)
四、操作题(每题6分,共24分)
23. 找一找。
24. 画一画。
(1)用数对表示A点的位置是______ 。
(2)过P点画AB边的垂线。
(3)画出△AOB绕点O逆时针旋转90°后的图形。
(4)按1:2画出△AOB缩小后的图形。
25. 折一折。
毕业在即,同学们用卡纸制作如图的“博士帽”。“博士帽”上面是边长30cm的正方形,下面是底面直径为18cm高为8cm的无盖无底的圆柱。
(1)制作一顶这样的“博士帽”至少需要卡纸多少平方厘米?
(2)如果得数保留整平方厘米数,你会选择第______ 种取近似值的方法。
第一种:四舍五入法。
第二种:进一法。
第三种:去尾法。
26. 测一测。
四个杯子中均装有一些水,如果把50g糖溶入水中,则含糖率最高的是第______ 杯。
五、解答题(每题6分,共30分)
27. 为有效开展“阳光体育”活动,希望小学计划购买篮球和足球共54个。如图的线段图表示的是篮球和足球的个数之间的关系。请你用多种方法列式解答。
方法一:
方法二:
28. 钢琴上有黑白相同的琴键共88个,其中白色琴键用来弹奏基本音级,黑色琴键则用来弹奏变化音级。明明数了之后发现白色琴键比黑色琴键数量的2倍少20个,黑色琴键有多少个?
29. 如表:在同一地点同一时间,测得的不同物体的高度和它的影长之间的关系。
物体高度/m
1
2
3
4
……
影长/m
0.6
1.2
1.8
2.4
……
(1)根据表中的数据,在如图中描出相应的点,并把它们用线连起来。
(2)如果一个物体高度是6.5米,这时它的影长是多少米?
(3)用数学的眼光来看成语“立竿见影”,即同一时刻同一地点,竿高和影长成______ 比例。
30. 我们通常依据等量关系列方程来解决问题,请将等量关系与对应方程连线:
甲、乙两个港口相距1200海里,一艘货轮每小时航行20海里,邮轮每小时航行30海里,货轮航行3小时后,邮轮相对开出,几小时后货轮和邮轮相遇?
解:设x小时后货轮和邮轮相遇。
31. 如今,很多人都是“手机不离手”。亮亮在社区进行了一项关于每天使用手机时长的抽样调查,并将调查结果绘制成如图两种统计图(不完整)。
(1)结合两幅统计图的数据,可算出一共调查了______ 人。
(2)将两幅统计图补充完整。
(3)结合统计图,写一写你的感想。
答案和解析
1.【答案】四十五点五 455000
【解析】解:4550000000=45.5亿
45.5亿读作:四十五点五亿
4550000000=455000万
故答案为:四十五点五亿,455000。
根据题意,先改写成用亿作单位的数,再读数,数的改写就是直接在原数的万位后面点上小数点,同时要在改写的小数后面写上“万”字,数的大小不变。
此题考查了数的改写和数的读法,要求学生掌握。
2.【答案】10 60 六
【解析】解:6÷10=3:5=915=60%=六成
故答案为:10,9,60,六。
根据已知的比,可以把比化成分数,再利用分数的基本性质把分数的分子和分母同时乘一个不为0的数,得到与它相等的分数,再利用分子除以分母求出除法算式、成数及百分数即可。
此题考查小数、分数、百分数之间的转化,根据它们之间的关系和性质进行转化即可。
3.【答案】向北走20km
【解析】解:如果将车子向南行驶10km记作+10km,那么−20km表示向北走20km。
故答案为:向北走20km。
此题主要用正负数来表示具有意义相反的两种量:如果向南走记为正,则向北走就记为负,−20km表示向北走20km。据此解答。
此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
4.【答案】25 15 40
【解析】解:梯形的面积:
(8−6+8)×5÷2
=10×5÷2
=25(平方厘米)
三角形面积:
6×5÷2
=30÷2
=15(平方厘米)
平行四边形面积:
8×5=40(平方厘米)
答:梯形面积是25平方厘米,三角形面积是15平方厘米,平行四边形面积是40平方厘米。
故答案为:25,15,40。
由图可知,梯形的上底为(8−6)厘米、下底为8厘米、高为5厘米,根据梯形的面积公式“S=(a+b)ℎ÷2”,代入数据计算出梯形的面积即可;三角形的底为6厘米、高为5厘米,根据三角形的面积公式“S=aℎ÷2”,代入数据计算出三角形的面积即可;平行四边形的底为8厘米,高为5厘米,根据平行四边形的面积公式“S=aℎ”,代入数据计算出平行四边形的面积即可。
解答本题需熟练掌握平行四边形、三角形和梯形的面积公式。
5.【答案】直角
【解析】解:1+1+2=4
180×24=90(度)
答:最大的内角是90度,所以这是个直角三角形。
故答案为:直角。
三角形的内角和是180度,先计算出三个内角的份数之和,再求出最大内角占内角和的几分之几,最后根据分数乘法的意义,计算出最大内角是多少,进而判断这是个什么三角形。
本题解题关键是掌握三个内角的份数之和是180度,熟练掌握按比例分配问题的解题方法。
6.【答案】14
【解析】解:14+14+14+12=14×5
故答案为:14。
因为12=14+14,所以14+14+14+12可以看作5个14的和,根据分数乘整数的意义,补充空缺的数字。
本题解题的关键是把14+14+14+12可以看作5个14的和,熟练掌握分数乘整数的意义。
7.【答案】10
【解析】解:5÷0.5=10(个)
答:从5里面连续减去10个0.5结果是0。
故答案为:10。
求从5里面连续减去几个0.5结果是0,就是求5里面有几个0.5,用除法计算。
本题解题的关键是根据除法的意义列式计算,熟练掌握小数除法的计算方法。
8.【答案】6 2
【解析】解:8÷(3+1)
=8÷4
=2(L)
2×3=6(L)
答:圆柱形容器的容积是6升,圆锥容器的容积是2升.
故答案为:6、2.
根据圆柱的体积公式:V=sℎ,圆锥的体积公式:V=13sℎ,因为等底等高的圆柱的体积是圆锥体积的3倍,所以等底等高的圆柱和圆锥的体积和是圆锥体积的(3+1)倍,根据已知一个数的几倍是多少,求这个数,用除法求出圆锥容器的容积,进而求出圆柱容器的容积.
此题主要考查等底等高的圆柱与圆锥体积之间关系的灵活运用,关键是明确:等底等高的圆柱的体积是圆锥体积的3倍.
9.【答案】20 2.5 1:2000000
【解析】解:50÷20=2.5(厘米)
1厘米:20千米
=1厘米:2000000厘米
=1:2000000
答:图上的1cm表示实际距离20km,实际距离50km在图上要画2.5cm。把这个线段比例尺改写成数值比例尺是1:2000000。
故答案为:20,2.5,1:2000000。
根据线段比例尺可知:图上的1厘米表示实际距离20千米;实际距离是50千米,那么在图上应画多长,即求50千米里面有几个20千米,即画几厘米长;根据比例尺的含义:图上距离和实际距离的比,叫做比例尺,进行解答即可。
此题主要考查比例尺的意义以及图上距离、实际距离和比例尺之间的关系,解答时要注意单位的换算。
10.【答案】14 (4n+2)
【解析】解:1张桌子可以坐6人可以写成1×4+2人,
2张桌子可以坐10人可以写成2×4+2人,
2张桌子可以坐14人可以写成3×4+2人,
……
则n张桌子就可以坐(4n+2)人。
答:3张桌子坐14人,n张桌子可以坐(4n+2)人。
故答案为:14;(4n+2)。
根据题意,1张桌子可以坐6人可以写成1×4+2人,2张桌子可以坐10人可以写成2×4+2人……n张桌子就可以坐(4n+2)人,由此即可解决问题。
此类规律题一定要注意结合图形进行分析,发现规律:每多一张桌子,多坐4人,从而得出n张桌子可以坐(4n+2)人。
11.【答案】C
【解析】解:2+3<7,不能组成三角形;
3+3=6,不能组成三角形;
3+4>5,可以组成三角形;
2+4=6,不能组成三角形。
故选:C。
任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
本题考查了三角形的三边关系的应用。
12.【答案】A
【解析】解:分析可知,三组图形中,每组中的两个图形的运动方式分别是平移、旋转、轴对称。
故选:A。
平移是物体运动时,物体上任意两点间,从一点到另一点的方向与距离都不变的运动;旋转是物体运动时,每一个点离同一个点(可以在物体外)的距离不变的运动,称为绕这个点的转动;平移和旋转后图形的位置改变,但是形状、大小不变;依据轴对称图形的定义:一个图形沿一条直线对折,对折后的两部分都能完全重合,即可作答。
解答此题的关键是:应明确平移与旋转的意义和特征以及轴对称图形的特征,结合题意分析解答即可。
13.【答案】B
【解析】解:1既不是质数,也不是合数。
51的因数除了1和51,还有3和17。
91的因数除了1和91,还有13和7。
故选:B。
根据质数概念去判断,因数只有1和它本身的数是质数。
理解质数的概念是解题关键。
14.【答案】C
【解析】解:∠B=180°−90°−30°=60°,所以A岛的位置在B岛的南偏西60°方向,距离4千米处。
故选:C。
根据直角三角形的特征及三角形的内角和是180°可知,∠B=180°−90°−30°=60°,结合上北下南左西右东的图上方向,分析解答即可。
本题考查了方向与位置知识,结合直角三角形的特征及三角形的内角和是180°,分析解答即可。
15.【答案】D
【解析】解:用6个同样的正方体拼成一个立体图形,从正面、上面和左面看到的形状都是。
故选:D。
根据题意,从正面、上面和左面看到的形状都是2层,上层2个小正方形,下层2个小正方形,据此解答即可。
本题考查了从不同方向观察物体和几何图形,培养了学生的观察能力。
16.【答案】D
【解析】解:设n等于1.5。
n²=1.5×1.5=2.25
1n=11.5=23
23<1.5<2.25,所以1n
让n等于一个具体数,且大于1小于2,分别求出n、n²、1n是多少,再比较。
掌握分数大小的比较方法是解题关键。
17.【答案】C
【解析】解:由分析可得,求出这套茶具的价钱是:a+b×6=a+6b。
故选:C。
根据单价×数量=总价,求出6个茶杯的价钱,再用一个茶壶的价格加上6个茶杯的价钱,即可求出这套茶具的价钱;据此解答。
本题考查用字母表示数或数量关系。关键是找出数量间的等量关系。
18.【答案】B
【解析】解:A.垂直是一种特殊的相交,即相交包括垂直,关系正确,故不符合题意;
B.带分数只是假分数的一种形式,关系错误,故符合题意;
C.等边三角形是一种特殊的等腰三角形,即等腰三角形包括等边三角形,关系正确,故不符合题意;
D.长方形是一种特殊的平行四边形,正方形是一种特殊的长方形,即平行四边形包括长方形,长方形包括正方形,关系正确,故不符合题意。
故选:B。
在同一平面内,两条直线只有相交和平行这两种位置关系,垂直是一种特殊的相交;
分数按大小分为真分数和假分数,带分数只是假分数的一种形式;
等边三角形是三条边都相等的等腰三角形;
长方形是四个角都是直角的平行四边形,正方形是四条边都相等的长方形,据此解答。
本题考查了垂直和相交的关系、分数的分类、等边三角形和等腰三角形的关系,平行四边形和长方形的关系,长方形和正方形的关系。
19.【答案】C
【解析】解:选项A,4÷(4+1)
=4÷5
=0.8
=八折
原题说法正确;
选项B,k一定,则k+13是个定值,xy的乘积一定,x和y成反比例。原题说法正确;
选项C,等边三角形有3条对称轴,正方形有4条对称轴,半圆形有1条对称轴,对称轴条数最多的是正方形。原题说法错误;
选项D,掷硬币时,正面朝上的可能性为12,若掷150次,大约有75次正面朝上。原题说法正确。
故选:C。
选项A,“买四送一”,就是花4份的钱可以买到(4+1)份,据此计算后即可判断;
选项B,k一定,则k+13是个定值,xy的乘积一定,x和y成反比例;据此判断;
选项C,确定出等边三角形、正方形和半圆形的对称轴条数,即可确定哪种图形的对称轴条数最多;
选项D,根据“可能性”的知识判断即可。
解答本题需熟练掌握优惠方案的计算、会辨识两种相关联的量成什么比例、轴对称图形的对称轴条数的确定及根据可能性解决问题。
20.【答案】B
【解析】解:由分析可得,计算小数乘法、异分母加减法和分数乘法和推导圆柱的体积公式时,都运用了“转化”策略,而画对称轴图形时,没有运用“转化”策略。
故选:B。
A.计算第一个算式时把小数乘法转化为整数乘法,计算第二个算式时,把异分母分数加法转化为同分母分数加法,计算第三个算式时,把分数除法转化为分数乘法,都运用了“转化”策略;
B.画对称轴图形时,对称轴的另一半与原来的一半完全相同,不存在“转化”策略;
C.推导圆柱的体积公式时,把圆柱转化为长方体,运用了“转化”策略。据此解答。
本题考查“转化”策略的应用。关键是熟练掌握“转化”思想在数学中的运用。
21.【答案】解:(1)x−0.25=13
x−0.25+0.25=13+0.25
x=712
(2)3.6x=32.5
3x=2.5×3.6
3x÷3=2.5×3.6÷3
x=3
(3)23x−12x=512
16x=512
6×16x=512×6
x=52
【解析】(1)方程两边同时加上0.25;
(2)根据比例的基本性质,先把比例化为方程,两边再同时除以3;
(3)先把方程左边化简为16x,两边再同时乘6。
熟练掌握等式的基本性质和比例的基本性质是解题的关键。
22.【答案】解:(1)125×88
=(125×8)×11
=1000×11
=11000
(2)75.6+57+24.4+27
=(75.6+24.4)+(57+27)
=100+1
=101
(3)13.76−712−1.76−512
=(13.76−1.76)−(712+512)
=12−1
=11
(4)(7.5×3.14)÷(6.28×2.5)
=7.5×3.14÷6.28÷2.5
=(7.5÷2.5)÷(6.28÷3.14)
=3÷2
=1.5
(5)3.75×8.8+62.5×0.88
=8.8×(3.75+6.25)
=8.8×10
=88
(6)48×(1112−34+16)
=48×1112−48×34+48×16
=44−36+8
=16
【解析】(1)把88看成8×11,再按照乘法结合律计算;
(2)按照加法交换律和结合律计算;
(3)按照加法交换律和结合律以及减法的性质计算;
(4)按照乘法交换律和结合律计算;
(5)按照乘法分配律计算;
(6)按照乘法分配律计算。
本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
23.【答案】解:
。
【解析】根据图可知,0左边的数表示负数,一个大格表示−1;0右边的第一个括号表示把1平均分成了2份,其中的一份是12;第三个括号表示把1平均分成5份,其中的一份表示0.2,两份表示0.4;一个大格表示1,最后一空表示3。
明确题中一大格和一小格表示多少即可解答。
24.【答案】(6,5)
【解析】解:(1)用数对表示A点的位置是(6,5)。
(2)过P点画AB边的垂线。如图:
(3)画出△AOB绕点O逆时针旋转90°后的图形。如图:
(4)按1:2画出△AOB缩小后的图形。如图:
故答案为:(6,5)。
(1)根据用数对表示表示位置的方法,第一个数表示列,第二个数表示行,解答即可;
(2)根据垂线的画法,过P点画AB边的垂线即可。
(3)根据旋转的方法,点O不动,画出△AOB绕点O逆时针旋转90°后的图形即可。
(4)根据图形缩小的方法,把△AOB的底和高分别缩小到原来的12,画出△AOB缩小后的图形即可。
本题考查了数对表示位置、旋转、垂线的画法以及图形的缩小知识,结合题意分析解答即可。
25.【答案】二
【解析】解:(1)30×30+3.14×18×8
=900+3.14×144
=900+452.16
=1352.16(平方厘米)
答:至少需要卡纸1352.16平方厘米。
(2)应该选择第二种取近似值的方法。
故答案为:二。
(1)制作一顶这样的“博士帽”至少需要卡纸多少平方厘米就是求长方形面积加圆柱侧面积,根据正方形面积=边长×边长,圆柱侧面积=底面周长×高,代入数值计算即可解答;
(2)因为制作一顶这样的“博士帽”不能缺少卡纸,所以应该选择第二种取近似值的方法。
本题考查的是圆柱应用题,熟记公式是解答关键。
26.【答案】第三
【解析】解:3.14×(4÷2)2×6
=3.14×4×6
=75.36(立方厘米)
4×4×6
=16×6
=96(立方厘米)
13×3.14×(6÷2)2×6
=13×3.14×9×6
=56.52(立方厘米)
6×6×6=216(立方厘米)
56.52<75.36<96<216
答:含糖率最高的是第三杯。
故答案为:第三。
根据圆锥的体积公式:V=13 πr2ℎ,长方体的体积公式:V=abℎ,正方体的体积公式:V=a3,圆柱的体积公式:V=πr2ℎ,把数据代入公式求出四杯水的体积,然后进行比较,水少的含糖率就高。据此解答。
此题主要考查圆锥、圆柱、长方体、正方体体积公式的灵活运用,含糖率的意义及应用,关键是熟记公式。
27.【答案】解:方法一:54÷(1+45)
=54÷95
=30(个)
54−30=24(个)
方法二:设足球有x个,则篮球有45x个。
x+45x=54
95x=54
95x÷95=54÷95
x=30
当x=30时,45x=45×30=24
答:篮球有24个,足球有30个。
【解析】由线段图可知,篮球个数是足球个数的45,篮球和足球共54个。根据这个数量关系用两种方法解答即可。
本题考查了利用不同的方法解决同一个问题,体现了一题多解思想。
28.【答案】解:设黑色琴键有x个。
x+(2x−20)=88
3x−20=88
3x−20+20=88+20
3x÷3=108÷3
x=36
答:黑色琴键有36个。
【解析】设黑色琴键有x个,则白色琴键有(2x−20)个,合起来共88个,根据这个等量关系列方程解答。
利用方程解决问题的关键是找准题目中的等量关系。
29.【答案】正
【解析】解:(1)作图如下:
(2)6.5×0.6=3.9(米)
答:如果一个物体高度是6.5米,这时它的影长是3.9米。
(3)0.6÷1=0.6
1.2÷2=0.6
1.8÷3=0.6
……
因为影长与物体的高度的比值一定,所以同一时刻同一地点,影长与物体的高度成正比例。
故答案为:正。
(1)依据题目所给信息及表格中的数据,在如图中描出相应的点,并把它们用线连起来即可;
(2)根据图示可知,影长与物体的高度成正比例,如果一个物体高度是6.5米,这时它的影长是6.5×0.6=3.9(米),据此解答即可;
(3)依据比的意义写出比,因为影长与物体的高度的比值一定,所以影长与物体的高度成正比例,据此解答即可。
此题主要考查正比例的意义的实际应用,结合题意分析解答即可。
30.【答案】解:
【解析】根据方程中的等量关系连线即可。
利用方程解决问题的关键是找准题目中的等量关系。
31.【答案】200
【解析】解:(1)4÷2%
=4÷0.02
=200(人)
答:一共调查了200人。
(2)1−38%−2%−40%=20%
200×40%=80(人)
200×38%=76(人)
(3)手机方便了我们的生活,但是长时间看手机对眼睛有害。应该减少看手机的时间,避免产生“手机依赖症”。(答案不唯一)
(1)把调查的总人数看作单位“1”,用已知数÷对应的百分率,求出调查的总人数;
(2)用单位“1”减去1小时之内、3−5小时、5小时以上使用手机的人数占的百分率,求出1−3小时使用手机的人数占的百分数;用调查的总人数分别乘3−5小时、5小时以内使用手机人数占的百分率,求出它们的人数;将两幅统计图补充完整;
(3)结合统计图,写出自己的感想即可。
此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
2022年辽宁省鞍山市铁东区小升初数学试卷: 这是一份2022年辽宁省鞍山市铁东区小升初数学试卷,共18页。试卷主要包含了填空,选择,数学操作,数学应用等内容,欢迎下载使用。
2023年辽宁省鞍山市铁东区小升初数学试卷: 这是一份2023年辽宁省鞍山市铁东区小升初数学试卷,共28页。试卷主要包含了填一填,选一选,数学运算,数学操作,数学应用等内容,欢迎下载使用。
2023届辽宁省鞍山市铁东区三下数学期末联考试题含解析: 这是一份2023届辽宁省鞍山市铁东区三下数学期末联考试题含解析,共5页。试卷主要包含了填空题,选择题,判断题,计算题,解答题等内容,欢迎下载使用。













