人教版九年级上册24.1.1 圆完整版课件ppt

这是一份人教版九年级上册24.1.1 圆完整版课件ppt，共20页。PPT课件主要包含了第二十四章圆，∠AOA′，∠BOB′，仍重合，顶点在圆心上，有什么特点，圆心角∠AOB，利用旋转的特征，同样我们可得，圆心角相等等内容，欢迎下载使用。

24.1 圆的有关性质
24.1.3 弧、弦、圆心角
如何将圆形蛋糕平均分成四块，你会分吗？
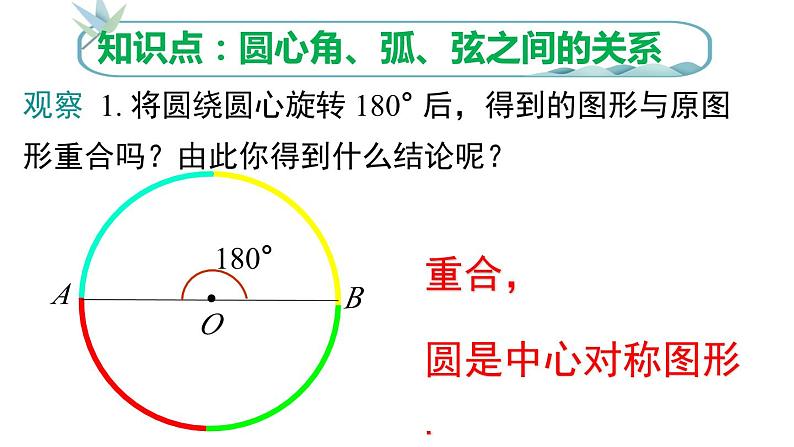
观察 1. 将圆绕圆心旋转 180° 后，得到的图形与原图形重合吗？由此你得到什么结论呢？
重合，圆是中心对称图形.
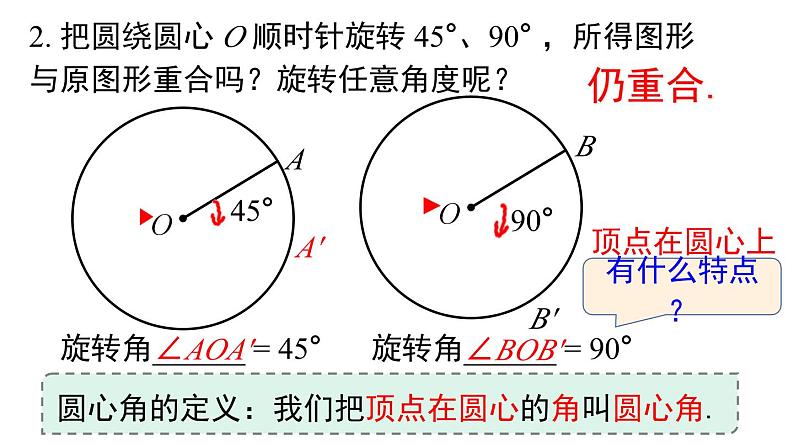
2. 把圆绕圆心 O 顺时针旋转 45°、90° ，所得图形与原图形重合吗？旋转任意角度呢？
旋转角______ = 45°
旋转角______ = 90°
圆心角的定义：我们把顶点在圆心的角叫圆心角.
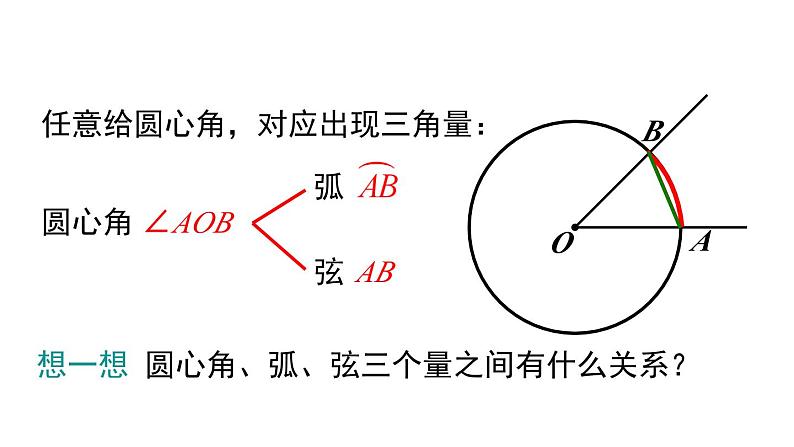
想一想 圆心角、弧、弦三个量之间有什么关系？
任意给圆心角，对应出现三角量：
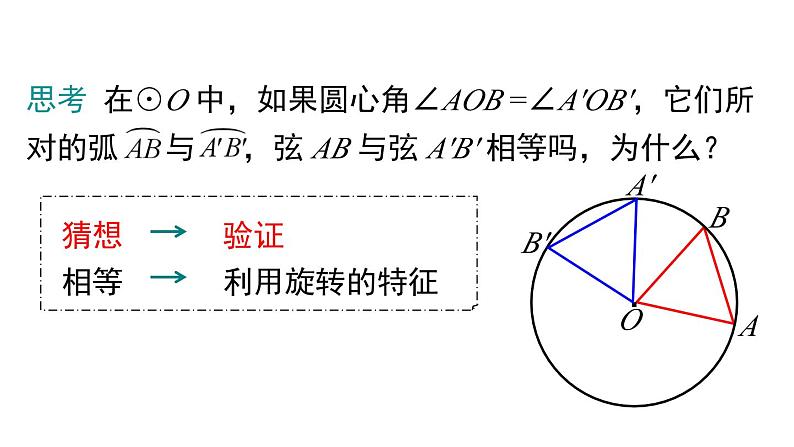
思考 在⊙O 中，如果圆心角∠AOB =∠A′OB′，它们所对的弧 与 ，弦 AB 与弦 A′B′ 相等吗，为什么？
证明：因为将圆绕圆心旋转任一角度都能与自身重合，所以可将⊙O 绕圆心旋转，使点 A 与点 A′ 重合.由于∠AOB =∠A′OB′，∴ 点 B 与点 B′ 重合.因此， 与 重合，AB 与 A′B′ 重合.即 ，AB = A′B′.
在等圆中，这个结论是否同样适用？
如图，在等圆中，如果圆心角 ∠AOB ＝∠A′O′B′，你发现的等量关系是否依然成立？
①∠AOB = ∠A′OB′
③ AB = A′B′
弧、弦与圆心角的关系定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．
在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角______，所对的弦______；在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角______，所对的优弧和劣弧分别______.
∴ AB = AC，即△ABC 是等腰三角形.
又∵∠ACB = 60°，
∴△ABC 是等边三角形，即 AB = BC = CA.
∴∠AOB =∠BOC =∠AOC.
例1 如图，在☉O 中， = ，∠ACB = 60°， 求证：∠AOB =∠BOC =∠AOC.
“同圆或等圆”这个前提可以去掉吗？
∠AOB = ∠COD
1.如图，在☉O 中， ，AD⊥OC 于 D. 求证：AB = 2AD.
证明：延长 AD 交 AD 于 E，∵ OC⊥AD，∴
∴ AB = 2AD.
1. 如果两个圆心角相等，那么 ( )A．这两个圆心角所对的弦相等B．这两个圆心角所对的弧相等C．这两个圆心角所对的弦和弧分别相等D．以上说法都不对
2. 如图，C 为 的中点，CN⊥OB 于 N，弦 CD⊥OA于 M，CN = 4 cm，则 CD =_______cm.
3. 如图，AB 为⊙O 的直径，C、D 是⊙O 上的两点，且 BD∥OC．求证： ．
证明：∵ OB = OD，∴∠D =∠B.∵ BD∥OC，∴∠D =∠COD，∠AOC =∠B.∴∠AOC =∠COD.